Матрица факторных нагрузок

;   • До каких пор (сколько раз) должна повторяться операция ;         вращения? ,;.   • Какой угол лучше установить для поворота?

Наиболее простым является ортогональное вращение. Оно производится умножением матрицы факторных нагрузок на некоторую ортогональную матрицу Т, задающую угол поворота, размерностью г х _г по числу общих факторов. Поворот может задаваться по или против часовой стрелки, например для матрицы факторных нагрузок А с числом общих факторов г = 2:

Если матрица факторных нагрузок содержит данные более чем по двум латентным факторам, строится несколько матриц преобразования Т для всех парных комбинаций факторов. Так, для трехмерной матрицы А будут использоваться три матрицы преобразования Т.

вращение против часовой стрелки:

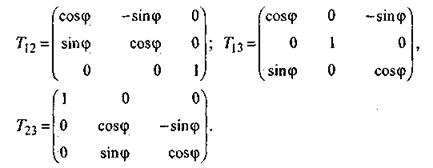
Полная матрица преобразования для трехмерного случая будет: Т= Т_]2х 71 з ^х /23- Этот подход обобщается на случай, когда число общих факторов г > 3, для четырехмерной матрицы А полная матрица преобразования Т будет произведением уже шести матриц вращения, для всех пар общих факторов:

Т = 71₂ х 71 з х 71₄ х Т₂₃ х Т_2Л х Т₃₄ и т. д.

При условии ортогонального вращения всегда 7" Т — Б.

Пример 7,6. Выполним однократный поворот двумерной матрицы факторных нагрузок, полученной методом главных компонент (п. 7.4.2). Пусть угол поворота будет равен 30° U<p =30°):

В результате вращения получена матрица факторных нагрузок, интерпретируемая проще исходной. В составе первой главной компоненты заметно определяющее значение признаков: ai, Х₂, во второй — Х₃. Одновременно выполняется требование АА' = WW. После перемножения нормированное пространство искажено, т.е. появляются элементы, большие единицы, и не обязательно ^wj_r = "kj . Чтобы вернуться к принятым пространственным соотношениям, достаточно нормализовать матрицу Wno известному правилу: векторы И⁷—матрицы факторного отображения

W,

после    поворота    W, = ——,

Wj

Построим график с исходным положением пространства главных компонент до и после поворота. В пространстве главных компонент точками показаны элементарные признаки JT_b Х_ъ Х₃ (рис. 7.14).

Косоугольное вращение матрицы факторных нагрузок может проводиться поочередным вращением каждого фактора на определенный угол или одновременным вращением всех факторов посредством умножения исходной матрицы нагрузок А на неор-