Матрица наблюдений.Модель дисперсионного анализа с главными эффектами. Проверка гипотез

Новосибирский государственный

технический университет

Кафедра прикладной математики и информатики

Лабораторная работа №1

по дисциплине: «Планирование и анализ экспериментов»

Факультет:            ПМИ

Группа:                 ПМ-83

Студенты:             Большакова А.

Журавлев В.

Миркин Е.

Моисеев Д.

Преподаватель:    Попов А.А.

Лисицын Д. В.

Новосибирск 2002

1. Задание.

По имеющимся данным сформировать матрицу наблюдений Х, постулировать модель дисперсионного анализа с главными эффектами (без взаимодействий уровней факторов). Провести редукцию модели к модели полного ранга, определить базис ФДО. По программе МНК-оценивания провести оценивание ФДО в редуцированной модели. Проверить гипотезы о незначимости вида Н₁, Н₂, Н₃, Н₄ для каждого фактора.

2. Постановочная часть.

Условия наблюдения за линейным объектом подчиняются линейному уравнению вида:

y=Xq+e, где y – наблюдаемый отклик, q - m-мерный вектор неизвестных параметров, подлежащих оцениванию по экспериментальным данным, Х – матрица наблюдения, е – случайна составляющая.

Используемый способ задания матрицы: каждый качественный фактор кодируется несколькими регрессорами по числу уровней данного фактора и принимает значение 1 и 0 в зависимости от присутствия данного фактора в эксперименте на соответствующем уровне.

Т.к. матрица наблюдений имеет дефект ранга, то не для любого параметра q_i существует единственная и несмещенная оценка. Но  существует ограниченный набор (базис) параметрических функций вида y=С^тq, для которых оценки y^{^} являются единственными и несмещенными – функции допускающие оценку (ФДО).

Исходная модель наблюдения:

y_ij…l=m+a_i+b_j+e_ij…l, i=1,2,3, j=1,2,3,4, где m – аддитивная постоянная, a_i –  эффекты уровней первого фактора, b_j – эффекты уровня второго фактора.

Тогда q=(m,a₁, a₁, a₂, a₃, b₁, b₂, b₃, b₄)^т.

В базис ФДО войдут следующие функции:

`m=m+a<sub>3</sub>+b<sub>4</sub>,`a₁=a₁-a₃,`a<sub>2</sub>=a<sub>2</sub>-a<sub>3</sub>,`b₁=b₁-b₄,`b<sub>2</sub>=b<sub>2</sub>-b<sub>4</sub>,`b₃=b₃-b₄.

После проведения редукции модели к модели полного ранга можно сформировать матрицу Х₀. В ее состав войдут линейно независимые столбцы матрицы Х: m,a₁, a₂, b₁, b₂, b₃.

Тогда можно вычислить оценку

`q^{^}=(X₀^т X₀)^–1 X₀^тy, учитывая, что  y=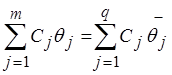 , , 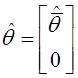где q=rgX₀, m – количество неизвестных.

Получаемая аппроксимирующая модель   .

3. Проверка гипотез о незначимости.

Н: С^т`q=t – общая линейная гипотеза.

Статистика F=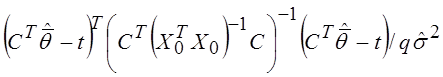, где q=rgC^T.  Если F>F_a,q,N-r , r=rg X₀, то гипотеза отвергается. Оценка дисперсии  вычисляется с учетом повторных наблюдений.       

Проверяемые гипотезы:

H1: `a1=0 – гипотеза о незначимости различий в эффектах 1-го и 3-го уровней фактора 1.

H2: `a2=0 – гипотеза о незначимости различий в эффектах 2-го и 3-го уровней

H3: `a1=a2 – гипотеза о незначимости различий в эффектах 1-го и 2-го уровней фактора 1.

Н4: `b1=0 – гипотеза о незначимости в эффектах 1-го и 4-го уровней фактора 2.

фактора 1.

H5: `b2=0 – гипотеза о незначимости различий в эффектах 2-го и 4-го уровней фактора 2.

H6: `b3=0 – гипотеза о незначимости различий в эффектах 3-го и 4-го уровней фактора 2.

H7: `b1=`b2 – гипотеза о незначимости различий в эффектах 1-го и 2-го уровней фактора 2.

H8: `b1=`b3 – гипотеза о незначимости различий в эффектах 1-го и 3-го уровней фактора 2.

H9: `b2=`b3 – гипотеза о незначимости различий в эффектах 2-го и 3-го уровней фактора 2.

H10: `a1-2*`a2=0 – гипотеза о незначимости кривизны линии отклика y.

H11: `b1-2*`b2=0 – гипотеза о незначимости кривизны линии отклика y.

H12: `b2-2*`b3=0 – гипотеза о незначимости кривизны линии отклика y.

4. Компьютерный листинг и результаты расчетов.

, .

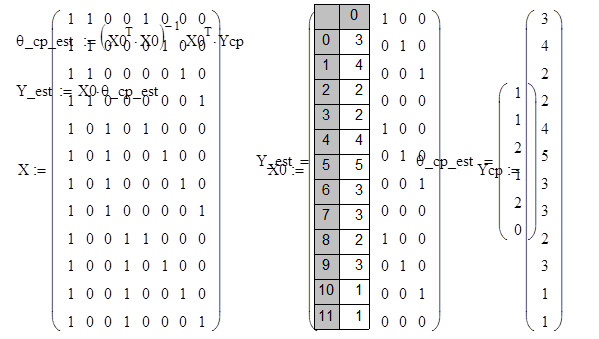
Расчет дисперсии по повторным наблюдениям:

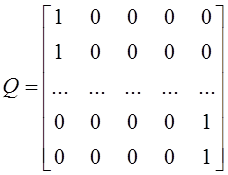
Количество опытов N=24, число неизвестных m=6.

f_R=N-m=18

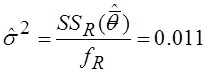
Проверка гипотез:

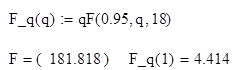Н1: `a1=0

Т.к. F>F_q, значит, a1 ¹ a3, т.е. вклады  этих двух уровней  в отклик у различны.

Н2: `a2=0

          Аналогично, вклад с уровней 2 и 3 различимы для у.

Н3: `a1=`a2

Гипотеза отвергается, значит, различия в эффектах 1 и 2 уровней фактора 1 значимы.

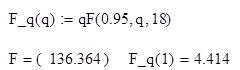Н4: `b1=0

Гипотеза отвергается.

Н5: `b2=0

Гипотеза отвергается.

Н6: `b3=0

Эта гипотеза принимается, т.е. b3=b4, и значит, вклады этих двух уровней в отклик y неразличимы.

Н7: `b1=`b2

Гипотеза отвергается.

 Н8: `b1=`b3

Гипотеза отвергается.

Н9: `b2=`b3

Гипотеза отвергается.

Н10: `a1-2*`a2=0

Гипотеза отвергается, значит, зависимость отклика на этом участке нелинейная.

H11: `b1-2*`b2=0

Гипотеза отвергается, значит, зависимость отклика на этом участке нелинейная.

H12: `b2-2*`b3=0

Гипотеза отвергается, значит, зависимость отклика на этом участке нелинейная.

Статистические выводы:

По результатам проверки различных линейных гипотез относительно параметров q сделаны следующие выводы: вклады со всех уровней являются различимыми для отклика у, исключая уровни b3 и  b4, так как гипотеза о незначимости различий в эффектах 3 и 4 уровней (H6:`b3=0) принимается. Т.к. гипотеза о незначимости кривизны линии зависимости y от факторов отвергается, то эта зависимость не является линейной.