Комбинаторные методы

Комбинаторные методы.

Комбинаторные методы в своей основе исходят из конечности числа планов задачи, используют ее комбинаторный характер.  В основе лежит  идея не полного, а частичного перебора планов задачи. Т.е. при решении не рассматриваются некоторые подмножества вариантов, заведомо не дающих оптимума. Перебираются лишь те оставшиеся варианты, которые в определенном смысле являются перспективными. В отличие от методов отсечений, комбинаторные методы значительно меньше подвержены влиянию ошибок округления. Далее комбинаторные методы (большинство) не используют решение задачи линейного программирования, в которую могла бы быть погружена дискретная задача. Комбинаторные методы отличаются от методов отсечений более простой арифметикой, обладают более сложной логикой ветвления решения. Наибольшую чувствительность комбинаторные методы проявляют к размерности задачи. Количество вычислений быстро возрастает при увеличении размерности. Пожалуй, одним из достоинств комбинаторных методов является то, что нет необходимости в доказательстве их конечности, она бывает очевидна из существа задачи.

Центральное место среди комбинаторных методов занимают методы, общими для которых является идея метода “ветвей и границ”.

Конкретизация динамического программирования для ряда специфических дискретных задач тоже представляет собой комбинаторные методы (методы направленного перебора). Различные методы последовательных расчетов.

Наиболее подробно остановимся на методе ветвей и границ, особенно, алгоритме Литла, Сунни, Мурти и Кэрел для задачи о коммивояжере.

Впервые метод ветвей и границ был предложен в 1960г. в работе Лэнд и Дойг для задачи целочисленного линейного программирования. Затем она была несколько забыта и возродилась в 1965г. в работе Литла, Сунни, Мурти и Кэрела для задачи о коммивояжере. Здесь и появилось название ветвей и границ.

Идея метода ветвей и границ.

Рассматривается задача дискретного программирования:

при .

G – конечное множество (некоторое).

В основе метода ветвей и границ лежат следующие построения, которые в ряде случаев позволяют существенно снизить объем перебора.

I.  Вычисление нижней границы (оценки).

Часто удается найти нижнюю границу (оценку) целевой функции f на множестве планов G (или на некотором подмножестве G’), т.е. такое число x(G) (или x(G’)), что для  имеет место

соответственно для  будет

II.  Разбиения на подмножества (ветвление).

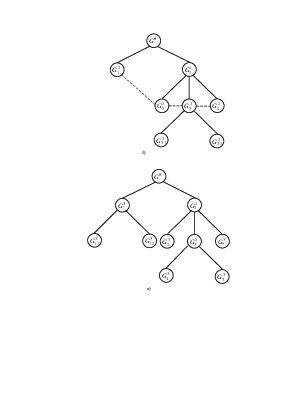
Реализация метода связана с постепенным разбиением множества планов G на дерево подмножеств (ветвлением). Ветвление происходит по следующей многошаговой схеме.

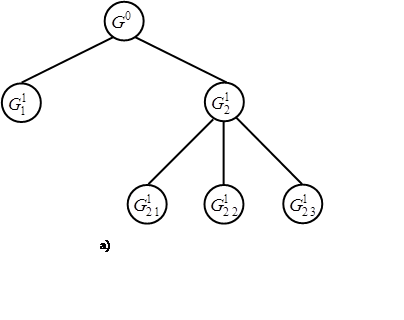
Начальный 0–й шаг. Имеется множество G⁰ = G.  Некоторым способом оно разбивается на конечное число (обычно не превосходящее подмножеств G₁¹, G₂¹ ,…, G_r1¹).

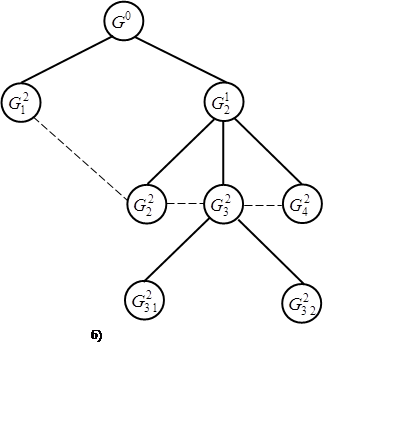
k–й шаг ( k > 0). Имеются множества G₁^k, G₂^k ,…, G_rk^k, еще не подвергавшиеся ветвлению. По некоторому правилу среди них выбирается наиболее перспективное множество G_n(k)^k и разбивается на конечное число подмножеств:

Еще не подвергавшиеся разбиению множества

заново обозначаются через

Схематично такой процесс можно представить следующим образом:

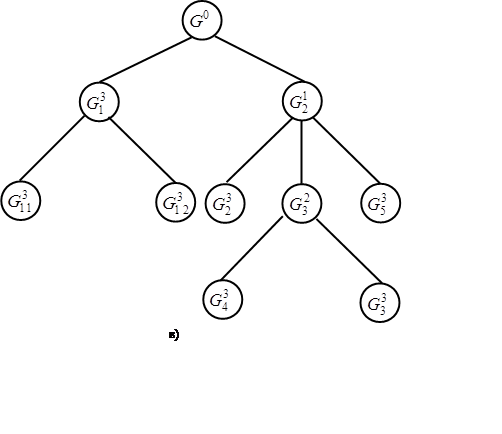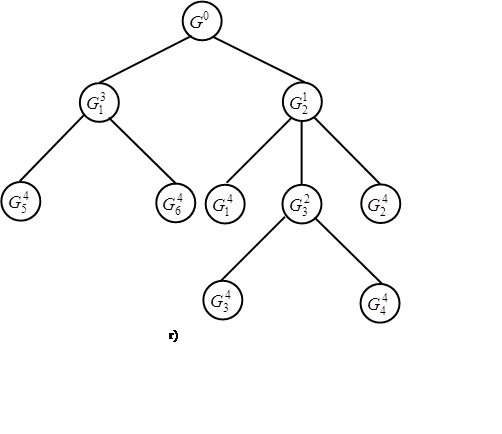III.  Просчет оценок.

Если множество G₁ Ì G₂, то, очевидно,

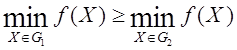
Поэтому, разбивая в процессе решения некоторое множество G на подмножества G'₁, G'₂, …, G'_s,  

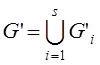
всегда будем считать, что оценка (граница) для любого подмножества G_i’ не меньше оценки для множества G_i :

x(G'_i) ³ x(G')

В конкретных ситуациях часто оказывается возможным добиться улучшения оценки, т.е. получить хотя бы для некоторых i строгое неравенство

x(G'_i) > x(G')

IV.  Вычисление планов.

Для конкретных задач могут быть указаны различные способы нахождения планов в последовательно разветвляемых подмножествах. Любой такой способ существенно опирается на специфику задачи.

V.  Признак оптимальности.

Пусть 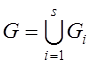и план  принадлежит некоторому подмножеству G_n.

Если при этом

, i = 1, 2,…, s.

то оптимальный план задачи 1 – 2. (Доказательство непосредственно следует из определения оценки).

Обычно этот признак применяется на некотором этапе ???????

VI.  Оценка точности приближенного решения.

Пусть ,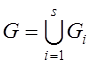

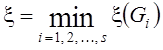
Если  некоторый план исходной задачи (т.е. ), то

(Доказательство следует из определения оценки).

Очевидно, что если разность  невелика, то  можно принять за приближенное решение, а D – за оценку точности приближения.

Формально схема метода “ветвей и границ” описывается следующим образом:

0 – шаг. Вычисляем оценку . Если при этом удается найти такой план , что

то – оптимальный план.

Если оптимальный план не найден, то по некоторому способу разбиваем множество G = G⁰ на конечное число подмножеств

и переходим к 1–му шагу.

1 – шаг. Вычисляем оценки , i = 1, 2,…, r₁. Если при этом удается найти такой план , что  для некоторого r (1 £ r £ r₁) и

, i = 1, 2,…, r₁.

то – оптимальный план.

Если же оптимальный план не найден, то выбираем “наиболее перспективное“ для дальнейшего разбиения множество  по следующему правилу

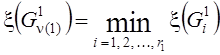
Разбиваем множество  на несколько (обычно не пересекающихся) подмножеств:  ??????????

Еще не подвергающиеся разбиению множества

заново обозначим через

и переходим к 2 – му шагу.

 k – шаг. (k ³ 2). Вычисляем оценки , i = 1, 2,…, r_k. Если при этом удается найти такой план , что  для некоторого r (1 £ r £ r_k) и

, i = 1, 2,…, r_k.

то – оптимальный план.

Если же оптимальный план не найден, то снова выбираем “наиболее перспективное“ множество  по следующему правилу

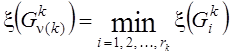
Разбиваем множество  на несколько (обычно не пересекающихся) подмножеств:  

Еще не подвергающиеся разбиению множества

заново обозначим через

и переходим к (k + 1) – му шагу.

Для реализации этой схемы методы ветвей границ для конкретных задач дискретного программирования, исходя из особенностей этих задач