














































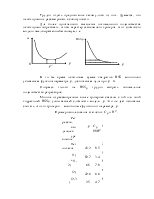








иметь нормированное нормальное распределение (с единичной дисперсией). Таким образом пункт б) доказан.
Оценивание при наличии линейных ограничений.
Пусть модель имеет вид:
![]() , где
, где ![]() -
матрица
-
матрица ![]() ранга
ранга ![]() .
Предположим, что мы хотим найти оценки параметра
.
Предположим, что мы хотим найти оценки параметра ![]() ,
минимизируя
,
минимизируя ![]() , при наличии линейных ограничений
, при наличии линейных ограничений ![]() , где
, где ![]() -
известная
-
известная ![]() матрица, а
матрица, а ![]() -
известный вектор
-
известный вектор ![]() .
.
Применим метод множителей Лагранжа. Рассмотрим выражение: ![]() , где
, где ![]() -
вектор множителей Логранжа. Решим уравнения:
-
вектор множителей Логранжа. Решим уравнения:
![]() (2.1)
(2.1)
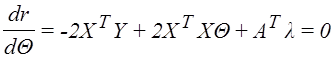 (2.2)
(2.2)
Решения уравнений (2.1) и (2.2) обозначим через ![]() и
и ![]() . Тогда
из (2.2) получаем:
. Тогда
из (2.2) получаем:
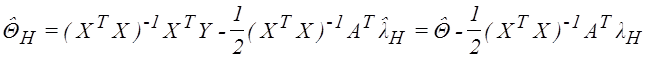 , а из (2.1):
, а из (2.1):
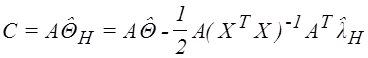 .
.
Поскольку матрица ![]() - п.п.о., то матрица
- п.п.о., то матрица ![]() будет п.п.о. ранга
будет п.п.о. ранга ![]() .
Следовательно
.
Следовательно
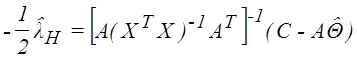 .
.
Окончательно подставляя в (2.3):
![]() . (2.4)
. (2.4)
Общая линейная гипотеза.
Пусть мы хотим проверить гипотезу H:
![]() , где
, где ![]() - известная
- известная ![]() матрица,
матрица,
![]() - известный
- известный ![]() вектор.
вектор.
Обозначим:
![]() и
и
![]()
где ![]() нами вычислен в виде (2.4).
Таким образом
нами вычислен в виде (2.4).
Таким образом ![]() - минимальное значение
- минимальное значение ![]() при ограничениях
при ограничениях ![]() .
.
Теорема 2.3.
1. ![]() доказать самостоятельно.
доказать самостоятельно.
2. ![]()
3. Если гипотеза H верна, то статистика
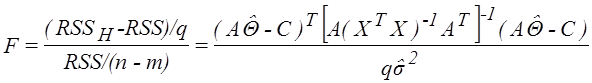 (2.5)
имеет распределение
(2.5)
имеет распределение ![]() гипотеза H
принимается если
гипотеза H
принимается если ![]() , где
, где ![]() -
критическая точка.
-
критическая точка.
4. Если ![]() , то статистика
, то статистика ![]() принимает вид:
принимает вид:
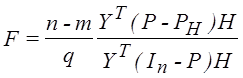 , где
, где ![]() - симметричная и идемпотентная
матрица и
- симметричная и идемпотентная
матрица и ![]() ,
,
![]() .
.
Частный случай: проверка значимости параметра H: ![]() или H:
или H: ![]() , где
, где ![]() -
вектор-строка, в которой на j-ом месте стоит 1, на
остальных местах – нули. Обозначим
-
вектор-строка, в которой на j-ом месте стоит 1, на
остальных местах – нули. Обозначим ![]() - j-ый
диагональный элемент. Тогда:
- j-ый
диагональный элемент. Тогда:
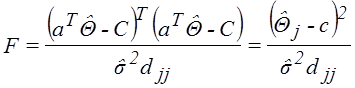 (2.6)
имеет при гипотезе H распределение
(2.6)
имеет при гипотезе H распределение ![]() .
.
Доверительное оценивание.
Совместное доверительное оценивание параметрических функций.
Проверку гипотезы H в теореме 2.3 можно трактовать следующим образом:
![]() , (2.7)
т.е. вероятность того, что случайная величина
, (2.7)
т.е. вероятность того, что случайная величина 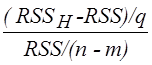 не
превзойдет некоторого наперед заданного положительного числа,
не
превзойдет некоторого наперед заданного положительного числа, ![]() равна
равна ![]() , где
, где ![]() ,
, ![]() .
.
Обозначим ![]() ,
, ![]() . Если принять, что
. Если принять, что ![]() мы
знаем, а вектор
мы
знаем, а вектор ![]() нам неизвестен, то неравенство в
фигурных скобках (2.7) можно трактовать как поверхность и внутренность
нам неизвестен, то неравенство в
фигурных скобках (2.7) можно трактовать как поверхность и внутренность ![]() - мерного эллипсоида с центром в точке
- мерного эллипсоида с центром в точке ![]() :
:
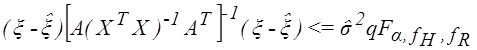 . (2.8)
. (2.8)
Размеры эллипсоида определяются величиной, стоящей в правой
части неравенства (2.8), а его конфигурация зависит от матрицы ![]() . Вероятность того, что эллипсоид покрывает
вектор истинных параметрических функций
. Вероятность того, что эллипсоид покрывает
вектор истинных параметрических функций ![]() равна
равна ![]() .
.
Рассмотрим частный случай ![]() , тогда
неравенство (2.8) преобразуется к виду:
, тогда
неравенство (2.8) преобразуется к виду:
![]() . (2.9)
. (2.9)
Неравенство (2.9) выражает поверхность и внутренность
доверительного эллипсоида для всех параметров с центром в точке ![]() , который с вероятностью
, который с вероятностью ![]() накрывает вектор истинных значений всех
параметров.
накрывает вектор истинных значений всех
параметров.
Доверительное оценивание для отдельного параметра.
Доверительный интервал для отдельного параметра также можно получить исходя из общего выражения (2.8) и пользуясь (2.6):
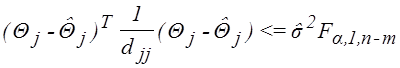 (2.10)
(2.10)
Учитывая, что ![]() , и что
, и что ![]() , где
, где ![]() -
- ![]() -критерий Стьюдента,
-критерий Стьюдента, ![]() , то (2.10) можно записать в виде:
, то (2.10) можно записать в виде:
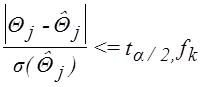 .
.
Или в виде двухстороннего неравенства:
![]() .
.
Доверительное оценивание для математического ожидания.
Аналогично можно записать интервальную оценку для ![]() истинного значения математического ожидания
функции отклика в точке
истинного значения математического ожидания
функции отклика в точке ![]() .
.
Имеем:
![]() /
/
С учетом (2.11):
![]() , (2.12)
где
, (2.12)
где ![]() ,
, ![]() .
.
Для ![]() :
: ![]() .
.
В качестве ![]() используется подходящая
оценка (см. предыдущую лекцию).
используется подходящая
оценка (см. предыдущую лекцию).
Проверка значимости уравнения регрессии.
Пусть задана линейная модель:
![]() ,
, ![]()
и требуется установить является ли регрессия с заданными
регрессорами значимой, т.е. мы хотим проверить гипотезу H:
![]() .
.
Гипотеза H имеет вид: ![]() , где
, где ![]() -
- ![]() матрица ранга
матрица ранга ![]() .
Применима общая теория с
.
Применима общая теория с ![]() ,
, ![]() и
и 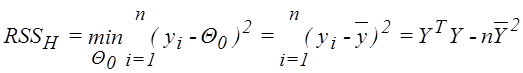 .
.
Оценивание параметров линейной регрессионной модели в условиях повторных наблюдений
Рассмотрим более общий случай, когда среди опытов, входящих в эксперимент, имеются повторные.
Без ограничения общности можно сгруппировать опыты по сериям так чтобы каждая из них содержала все повторные опыты, которые проведены при одних и тех же условиях.
Положим, что всего имеются Nc серий и в каждую v - ю
серию входят rv
- повторных опытов, ![]() . Общее число опытов
. Общее число опытов 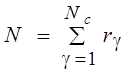
Поэтому F статистика занимается
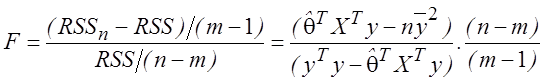 , (2.12)
, (2.12)
и ![]() если гипотеза H
верна (2.13).
если гипотеза H
верна (2.13).
Если гипотеза H отвергается, то это
означает, что регрессия значима и переменные ![]() нельзя
пренебрегать. (Регрессия значима – значит, её нельзя свести к уравнению
нельзя
пренебрегать. (Регрессия значима – значит, её нельзя свести к уравнению ![]() .). В то же время отклонения H вовсе не означает, что модель
.). В то же время отклонения H вовсе не означает, что модель ![]() ,
действительно адекватна.
,
действительно адекватна.
Как и раньше рассматриваем
линейную модель наблюдения ![]() (2.14)
(2.14)
Или в матричной форме ![]() (2.15)
(2.15)
Будем считать, что элементы векторов ![]() и
строки матрицы X сгруппированы его сериям.
Введем матрицу усреднения
и
строки матрицы X сгруппированы его сериям.
Введем матрицу усреднения
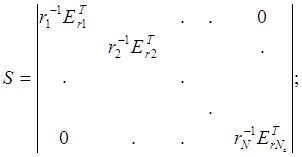 размером Nс
* N , где
размером Nс
* N , где ![]() - вектор столбец размерности
- вектор столбец размерности ![]() , соcтоящий из
единиц. Из структуры этой матрицы видно, что
, соcтоящий из
единиц. Из структуры этой матрицы видно, что
![]()
![]() (2,16),
(2,16),
где R - диагональная матрица весов,
впрягающая распределения опытов его сериям. Умножим теперь левую и правую часть
(2.15) слева на матрицу S и получим ![]() . Легко понять, что вектор
. Легко понять, что вектор ![]() в качестве элементов имеет среднее
значения отклика по сериям:
в качестве элементов имеет среднее
значения отклика по сериям:
![]() , причем,
, причем,
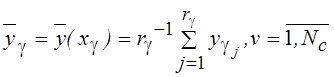
Матрица ![]() содержит
содержит ![]() строк, которые отличаются друг от друга и
соответствуют разным сериям:
строк, которые отличаются друг от друга и
соответствуют разным сериям:
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Вектор усреднённых ошибок имеет вид ![]()
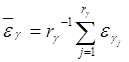 ,
, ![]()
Учитывая, что
![]()
![]()
Получим
![]()
![]()
Сумму взвешенных средних квадратичных отклонений для модели (2.15) можно записать в виде квадратичной формы
![]()
Опуская сомножитель ![]() ,
запишем
,
запишем
![]() (2.18)
(2.18)
Для модели (2.17) аналогичная мера рассогласования будет иметь вид
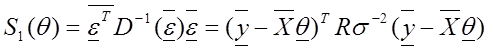
Опуская ![]() , запишем
, запишем
![]() (2.19)
(2.19)
Матрица весов R может быть представлена в виде произведений
R=QT Q, (2.20)
где Q- матрица размером N * Nc
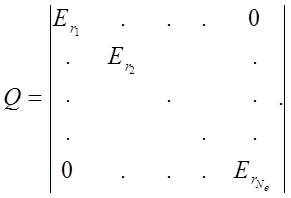 , где
, где ![]() - столбец единиц
- столбец единиц
Подставляя (2.20) в (2.19) получим
![]() , (2.21)
, (2.21)
где вектор ![]() – имеет уже N – составляющих, как и вектор
– имеет уже N – составляющих, как и вектор ![]() .
.
Суммы SS(q) и SS1(q) связаны между собой. Используя перегруппировку слагаемых первой суммы, можно показать, что
![]() , где
, где ![]() и не зависимы от
и не зависимы от ![]() .
Поэтому совершенно безразлично какой мерой рассогласования пользоваться для
отыскания оценок параметров: (2.18), (2.19) или (2.21).
.
Поэтому совершенно безразлично какой мерой рассогласования пользоваться для
отыскания оценок параметров: (2.18), (2.19) или (2.21).
Точечную оценку дисперсии ошибки эксперимента в случае,
когда имеется повторные опыты лучше всего определять через сумму (2.23) по
формуле ![]() , где
, где ![]() число
степеней свободы суммы SSe , равное
число
степеней свободы суммы SSe , равное
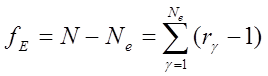 . Оценка
. Оценка ![]() есть
не что иное, как объединенная оценка выборочных дисперсий ошибки опыта, которые
можно найти по результатам отдельных серий повторных опытов.
есть
не что иное, как объединенная оценка выборочных дисперсий ошибки опыта, которые
можно найти по результатам отдельных серий повторных опытов.
Оценка дисперсии ошибки в g- ой серии повторных опытов равна
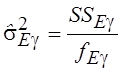 , где
, где 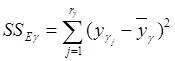 ,
,
![]() .
.
Отсюда следует, что объединенная оценка по всем сериям имеет вид
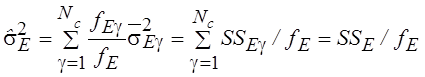 . (2.23)
. (2.23)
Заметим, что оценка ![]() определяется
независимо от модели.
определяется
независимо от модели.
При вычислении суммы SSe никак не используются параметры модели и несущественно, какому распределению подчиняются отклики.
При ![]() имеется следующие
соотношения:
имеется следующие
соотношения:
![]() (2.24) где SSE - остаточная сумма со степенями свободы
(2.24) где SSE - остаточная сумма со степенями свободы ![]()
![]() - мера степени неадекватности
представления экспери
ментальных данных с помощью выбранной модели. Она оценивает рассеивания средних
значений отклика по сериям относительно расчетной регрессивной зависимости с
учётом весов (Lack of fit –
неадекватность).
- мера степени неадекватности
представления экспери
ментальных данных с помощью выбранной модели. Она оценивает рассеивания средних
значений отклика по сериям относительно расчетной регрессивной зависимости с
учётом весов (Lack of fit –
неадекватность).
Оценка дисперсии на основе суммы SSLF вычисляется по формуле
![]() ,
, ![]() (2.25)
(2.25)
Оценка величины ![]() на основе SSR выражается отношением
на основе SSR выражается отношением
![]() ,
, ![]() .
.
Оценка величины ![]() является, по существу,
объединённой.
является, по существу,
объединённой.
Используя (2.24) и учитывая, что ![]() можно
записать
можно
записать
![]() .
.
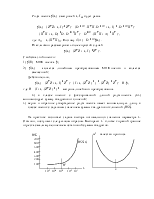
Проверка адекватности модели
Одной из важных гипотез, проверяемых в регрессионном анализе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.