Дисперсионный анализ. Определение и оценивание базиса ФДО.

Вариант задания

Примечание: в ячейках таблицы располагаются значения отклика, полученные в двух параллельных наблюдениях.

Решение

1.  По имеющимся данным сформировать матрицу наблюдений , постулировать модель дисперсионного анализа с главными эффектами (без взаимодействий уровней факторов).

В нашей задаче участвуют 2 фактора с тремя и четырьмя уровнями варьирования. Тогда матрица  будет иметь следующий вид:

.

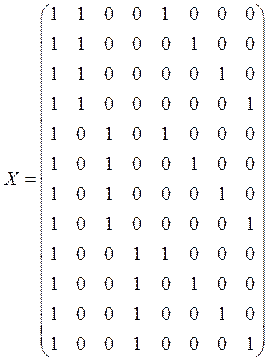Модель:

Пусть - среднее значение  в подпопуляции (по уровню фактора 1 и уровню фактора 2). Введем понятие генерального среднего , как:

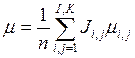, где 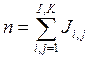, K=4, I=3 и - число наблюдений в  подпопуляции ( из условий задачи =2 ).

Для нашего варианта имеем: n=24, 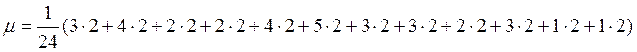=2,75

Тогда дифференциальные(главные) эффекты уровня можно ввести как:

, при ,

, при , .

Модель ДА имеет вид:

,                      (1.1)

где - аддитивная постоянная (генеральное среднее), - эффект -го уровня первого фактора, - эффект -го уровня второго фактора , - ошибка эксперимента, распределенная по .

Представим эту модель в виде :

, , .

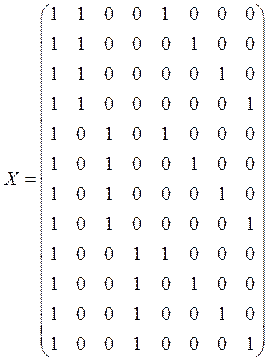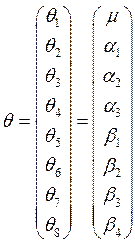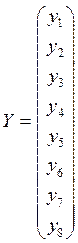2.  Провести редукцию модели к модели полного ранга, определить базис ФДО.

1)

Воспользуемся утверждением 1: в линейной модели для факторов без взаимодействий внутренний дефект ранга матрицы равен .

Значит, в нашей модели (1.1)  внутренний дефект равен 2.

Поскольку имеется определенная свобода выбора этих столбцов, то будем считать линейно зависимыми от других столбцы ,. В модели (1.1) в связи с ее внутренним дефектом ранга несмещенно будут оцениваться только  линейно независимых функций, допускающих оценку (ФДО), образующих базис ФДО.

Для построения базиса ФДО воспользуемся утверждением 2. В итоге получим, что базис ФДО составляют функции:

,  , .

.

2)

Редуцирование модели (1.1) к модели полного ранга можно проводить через факторизацию матрицы , где - матрица полного строчного ранга, равная:

.

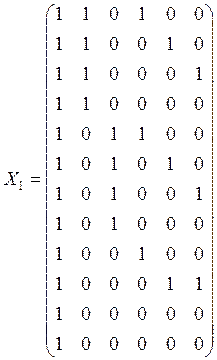                                        (1.2)

В (1.2) матрица задает вид базиса ФДО и имеет вид:, .

В нашей задаче:                                            

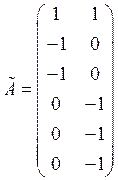 и соответственно .

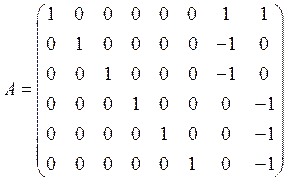В числе ФДО будут:

, а также их линейные комбинации.

3.  По программе МНК-оценивания провести оценивание ФДО в редуцированной модели. Проверить гипотезы о незначимости различий в эффектах для каждого фактора и фактора в целом.

Чтобы найти оценки для ФДО  достаточно применить теорему Гаусса-Маркова для модели (1.2): . Оценки параметров, соответствующие исключенным из модели линейно зависимым столбцам (регрессорам), автоматически считаются равными нулю.

Воспользовавшись средствами лабораторной работы№2 были получены следующие оценки для ФДО: .

Проверка гипотез о незначимости различий эффектах 1-го фактора:

Гипотеза о незначимости эффектов первого и второго уровней первого фактора формулируется как . Поскольку в редуцированной модели на месте параметра  оценивается сравнение (ФДО), то для проверки этой гипотезы достаточно проверить . Для проверки гипотезы  достаточно проверить . Для проверки гипотезы достаточно проверить гипотезу .

В листинге указаны все выкладки проверки гипотез. Основные результаты: показаны значимость эффектов первого и третьего, второго и третьего уровней первого фактора, незначимость эффектов первого и второго уровней.

Незначимость вцелом первого фактора может быть проверена по гипотезе: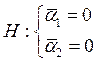. Проверка показала, что: первый фактор – значим.

Проверка гипотез о незначимости различий эффектах 2-го фактора:

Аналогичные действия проводим как и для первого фактора. Результаты: показаны значимость эффектов первого и четвертого, второго и четвертого, третьего и четвертого уровней второго фактора, незначимость эффектов первого и второго, второго и третьего уровней. Второй фактор вцелом – значим.

Министерство образования и науки Российской Федерации

Новосибирский государственный технический университет

Кафедра прикладной математики

Лабораторная работа №8

по курсу

«Планирование и анализ экспериментов»

Факультет: ПМИ

Группа: ПМ-13

Вариант: 1

Студент:  Глухова М.

Царапкин В.

Преподаватели: Лисицын Д.В.

Ванюкевич О.А.

Новосибирск 2005