Алгоритм моделирования случайной величины с заданной плотностью распределения

1.  Задание

Найти моделирующее выражение и написать алгоритм моделирования для случайной величины x, имеющей заданную плотность распределения f(x):

1)  по методу обратной функции (далее обозначаем МОФ)

f(x)=1/2*|sin x|, xÎ[-p/2,p/2]

2)  по МОФ при немонотонной j(a)

f(x)=C*(1+2^1/3x), C=1/(1+2^–2/3), xÎ[0,1]

3)  с использованием порядковых статистик

f(x)= 6/5*(x²-x+1), xÎ[0,1]

4)  f(x)=C/(1+e^x), C=1/ ln 2, xÎ[0,µ]

5)  по методу суперпозиции

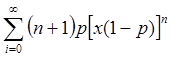
f(x)=

xÎ[0,1], 0<p<1

6)  по методу исключения

f(x)=3/4*(1+x²), x Î[0,1]

2.  Постановка задачи

Все методы моделирования сводится к преобразованию вида x=j(a₁, …, a_n), где a_i , i=1,…,n, независимые реализации равномерно распределенных псевдослучайных величин на отрезке [0,1].

 1.  Метод обратной функции (МОФ):

x=F^–1(a), где F(x) – функция распределения случайной величины x.

Для немонотонных преобразований j(a)=F^–1(a) моделирующее выражение можно строить на основе следующего утверждения.

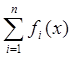Утверждение.

Пусть     f_n(x)=                           ,p_i=ò_-µ^µ f_i(x)dx,   F_i(x)= ò_-µ^x f_i(t)dt,

a₀=0, a_i=åⁱ_k=2 p_k, где f_i(x)>=0, i=1,…,n.

Тогда случайная величина x=F^–1_i(a–a_i–1) при a_i–1<=a<a_i имеет плотность распределения f_n(x).

2. Метод с использованием порядковых статистик:

Пусть f(x)=nC^k-1_n-1x^k-1(1–x)^n-k, xÎ(0,1), где n и k – некоторые натуральные числа. Тогда x – это k-я порядковая статистика для выборки a₁,…, a_n, a_iÎRav(0,1). Моделирование случайной величины x сводится к непосредственному моделированию a₁,…, a_n, с последующим их упорядочиванием , так что x=a_(k).

3. Метод суперпозиции:

Есть маргинальное распределение f_x(x) и надо построить моделирующее выражение для величины xÎ f_x(x,y). Для этого находятся маргинальная плотность распределения f_h(y), совместная плотность распределения  f(x,y) и условная плотность распределения f_x(x | y=h).

f(x,y)=  f_x(x,y),

f_h(y)= 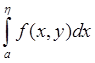, xÎ[a,b]

f_x(x | y=h) =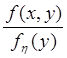

Тогда нахождение случайной велины происходит по следующему алгоритму:

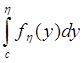1. a₁==Ф(h),  h=Ф^-1(a₁),  xÎ[c,d]
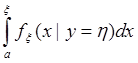2. a₂==F(x,h),  x=F^-1(a₂,h),  yÎ[a,b]

4. Метод исключения:

Для моделирования случайной величины x с плотностью распределения f(x), xÎ[a,b], выполняются следующие действия:

1. генерируются  2 случайные величины x₀ и h₀ такие, что x₀ÎRav[a,b] и h₀ÎRav[0,M];
2. если h₀>=f(x₀), тогда перейти к пункту 1;

иначе x=x₀.

М=max f(x), xÎ[a,b].

3.  Моделирующие выражения

1) x= arccos 2a, если aÎ[0,1/2) или  arcos 2*(1-a), если aÎ[1/2,1];

2) x= a/C, aÎ[0,C)

= (a*2^2/3/C)^1/2, aÎ[C,1],

C=1/(1+2^-2/3) ;

3) x= a₍₁₎, n=3, если aÎ[0,2/5) или a₍₂₎, n=2, если aÎ[2/5,1]:

4) M=1/ln 4;

5) величина h –  дискретна, поэтому используется модель моделирования дискретной величины, а не непрерывной.

hÎ P{h=n}=p(1-p)ⁿ.

x=a₂^{1 / (h+1)}

6) M=3/2.

4.  Проверка выборки.

Для того, чтобы проверить принадлежит ли выборка заданному распредеелению, используем критерий c² – Пирсона. Определим 2 гипотезы:

H₀ : F=F(x)

H₁ : F¹F(x), где F(x) – функция распределения заданной плотности.

Тогда для проверки строим статистику hi и проверяем, если она меньше, чем квантиль распределения c² (L–1, a), то гипотеза Н₀ справедлива и  выборка принадлежит заданному распределению, иначе надо отвергнуть гипотезу Н₁.

,

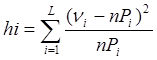где L – количество интервалов заданной области значений,

 - частота, равная количеству элементов, попавших в i-й интервал,

P_i= F(d_i+1) – F(d_i), где F(x) – заданное распределение,

a=P_H0{hi>} – вероятность отвергнуть данные при условии, что они верны (a – ошибка 1-го рода),

n – объем выборки.

5. Тесты

Построены графики зависимостей статистик hi и квантилей ss от количества интервалов L, на которые разбиты области значений случайных величин, где LÎ[2,29] и a=0.5.

Тест 1: для разных объемов

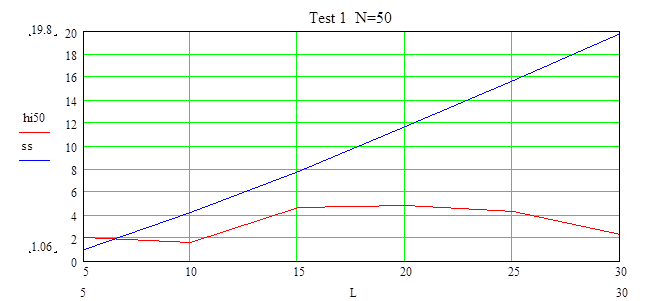
На графике видно, что выборка принадлежит заданному распределению с уровнем доверия a=0.9 при достаточно большом числе интервалов.

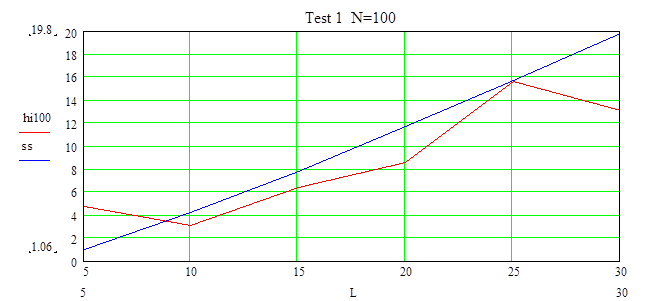
На  этом тесте видно, что при этом объема надо выбирать число интервалов больше 10, тогда гипотеза принимается с уровнем доверия a=0.9.

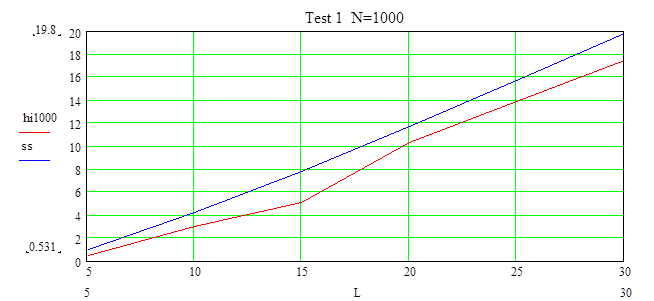
Данный объем достаточен для принятия гипотезы на любом числе интервалов при уровне доверия a=0.9.

Тест 2. для разных объемов выборки

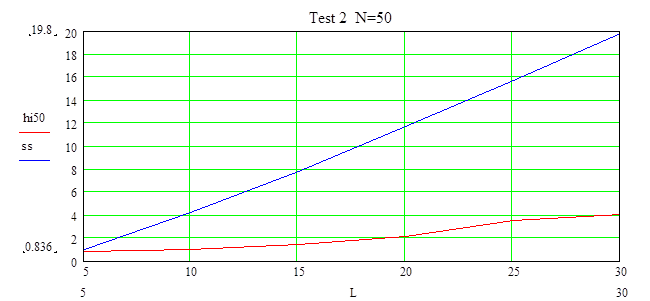
На графике видно, что при всех значениях L гипотезу о принадлежности к заданному распределению надо принять. Причем выборка распределена достаточно хорошо, т.е с уровнем доверия a>0.9.

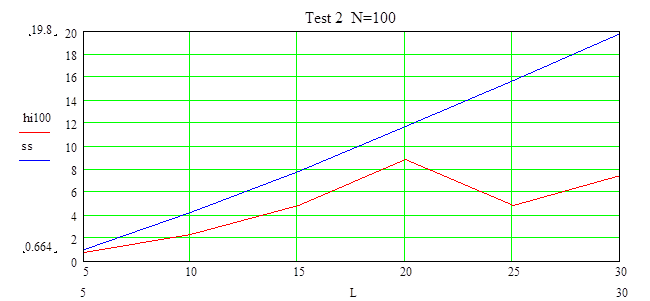
При данной объеме N=100 выборка принадлежит к заданному распределению при a=0.9 и  при увеличении значений L уровень доверия может быть выше.

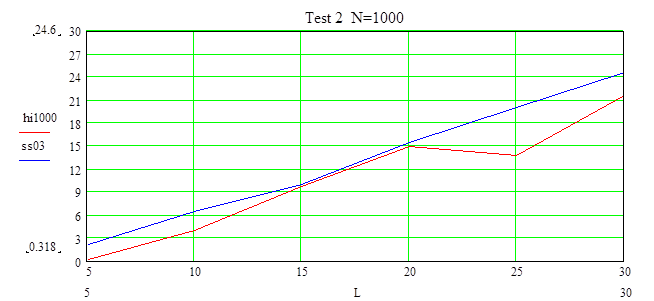
При объема N=1000 выборка принадлежит распределению при любом числе интервалов, но уровень доверия почти не может быть увеличен (только при L от 25 до30).

Тест 3. для разных объемов выборки

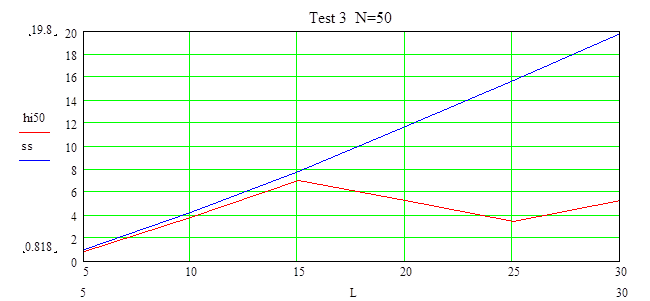
На числе интервалов от 5 до 15 выборка принадлежит распределению с уровнем доверия a=0.9, но при увеличении числа L уровень доверия повышается.

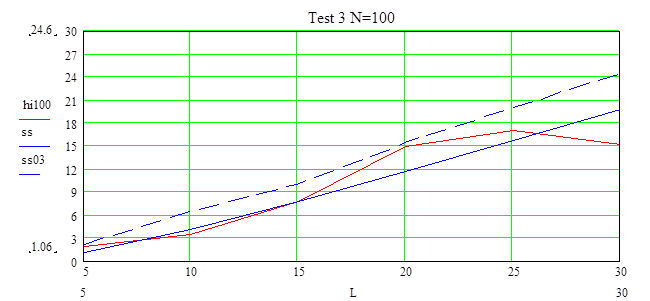
На этом графике видно, что при уровне доверия a=0.9 выборка принадлежит распределению только при L=10  и L=30, а при уменьшении уровня доверия до a=0.7 выборка полностью принадлежит заданному распределению на всех значениях числа интервалов, но это уже не очень хорошее значение уровня доверия.

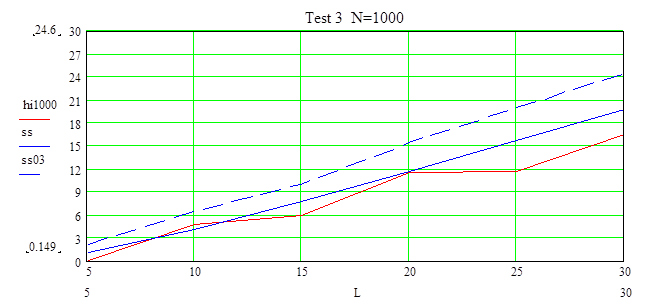
Этот график показывает принятие гипотезы о заданном распределении и при уровне доверия a=0.7 и при a=0.9 (на больших значениях L).