Лабораторная работа № 11. Нарезание зубчатых колёс червячной фрезой., страница 2

Измеренная высота витка инструментального червяка  позволит определить модуль m из формулы (11.12), а затем из формулы (11.11) вычислить коэффициент диаметра червяка q по измеренному диаметру вершин инструментального червяка. Делительный угол подъёма витка инструментального червяка:

                                                    (11.13)

Контрольные параметры цилиндрического прямозубого колеса

Геометрические параметры нарезаемого цилиндрического колеса определяют модулем m и параметрами стандартного исходного контура по  ГОСТ 13755: углом профиля α = 20º; коэффициентом высоты головки зуба = 1; коэффициентом радиального зазора с* = 0,25; коэффициентом радиуса переходной кривой = 0,38. В цилиндрических зубчатых колёсах вычисляют четыре диаметра: делительный, основной, вершин и впадин.

Делительный диаметр: - формула (10.6) из лаб. работы № 10.

Основной диаметр: - формула (10.8).

         Диаметр вершин: .                                          (11.14)

Диаметр впадин:                                     (11.15)   

Модуль цилиндрического зубчатого колеса стандартизирован. Извлечение из ГОСТ 9563 приведено в табл. 11.2.

Таблица 11.2. Модули m, мм

1-й ряд	1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20 … 80
2-й ряд	1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7 … 90

На чертежах деталей в таблице параметров указывают контрольные параметры зубчатых колёс. Контроль зубьев при изготовлении колёс осуществляют измерением размеров:

– длины общей нормали W;

– постоянной хорды ;

– высоты зуба до постоянной хорды .

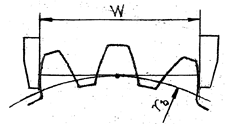
Рис. 11.2. Схема измерения длины общей нормали

Длину общей нормали W (рис. 11.2) измеряют обхватом губками штангенциркуля определенного числа зубьев z_w, зависящего от полного числа зубьев колеса z. Эта зависимость связана с недопустимостью кромочного касания зубьев или штангенциркуля, т.е. губки штангенциркуля своими плоскостями должны касаться эвольвентной поверхности зубьев. Число охватываемых зубьев в длине общей нормали z_w для прямозубых колес рассчитывают по зависимостям, приведенным в литературе, например, в [2], либо принимают из таблиц (табл. 11.3)

Таблица 11.3

Число зубьев колеса z	12–18	19–27	28–36	37–45	46–54	55–63	64–72	73–81
Число обхватываемых зубьев zw	2	3	4	5	6	7	8	9

Длину общей нормали рассчитывают по формуле:

W = (p (z_w – 0,5) – z inva) m·cosa.                                  (11.16)

Постоянную хорду и расстояние до постоянной хорды  (рис. 11.3) измеряют специальным инструментом — штангензубомером. Постоянная хорда — отрезок прямой, соединяющий две точки с разноимённых профилей зуба, на пересечении профилей с нормалями к ним, проведенными из точки пересечения оси симметрии зуба с делительной окружностью d:

 = 0,5pm cos²a .                                                   (11.17)

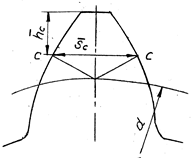
Рис. 11.3. Схема измерения постоянной хорды и высоты до постоянной хорды

Высоту до постоянной хорды  определяют как кратчайшее расстояние от вершины зуба до средней точки постоянной хорды:

                         = 0,5(d_a – d – tga).                                             (11.18)

Для определения модуля нарезанного зубчатого колеса по длине общей нормали используют следующие свойства эвольвенты:

1) нормаль, проведенная из любой точки эвольвенты, является касательной к основной окружности;

2) отрезок нормали к эвольвенте между точкой касания её с основной окружностью и точкой эвольвенты, равен длине дуги основной окружности.

Наиболее точным является метод определение модуля по разности длин общей нормали  и . Схема измерений и   приведена на рис. 11.4. Величину определяют обхватом  зубьев, - обхватом   зубьев. Основной шаг рассчитывают по формуле:

                                                    (11.19)

Искомый модуль  - по формуле:

                                                  (11.20)

Описание лабораторной установки

Общий вид лабораторной установки ТММ-СГУПС представлен на рис. 11.5. Она состоит из основания 1, по которому перемещается суппорт 2, поворотного устройства 3 с червячной фрезой 4 (инструментальным червяком), и заготовки 5. Ось червячной фрезы относительно оси заготовки имеет