Исследование линейных колебательных систем с одной и двумя степенями свободы. Исследование работы динамического гасителя колебаний.

Санкт-Петербургский Государственный Политехнический Университет

Лабораторная работа №1

Исследование линейных колебательных систем с одной и двумя степенями свободы. Исследование работы динамического гасителя колебаний.

                                                              Группа: 3031/2

                                                      Выполнили студенты:  Калганов О.С.

       Локтионова П.И.

                                                                                                   Полоротов Ю.В.

Рузанов Ю.

                                                                                        Тарасов М.

                                                                                        Яковлев П.

                                       Преподаватель:

Санкт-Петербург 2009 г

Цель работы: Исследование свободных колебаний системы с одной степенью свободы ( вибрационного стола без динамического гасителя колебаний). Исследование вынужденных колебаний системы с одной степенью свободы. Исследование вынужденных колебаний системы с двумя степенями свободы ( вибрационный стол с динамическим гасителем колебаний). Экспериментальное определение параметров установки.

Установка.

(Рис 1.)

Установка (Рис1.) представляет собой стол, ножки которого изготовлены из четырех пар стальных пластин 1. Пластины нижним концом жестко скреплены с фундаментом. На столе установлен небольшой электродвигатель постоянного тока 2, приводящий во вращение диск 3. С осью диска скреплена эксцентрично насаженная масса m.

При работе двигателя горизонтальная составляющая центробежной силы массы m вызывает колебания стола в горизонтальном направлении. Вертикальная составляющая не дает эффекта, так как жесткость системы в этом направлении во много раз больше, чем в горизонтальном направлении.

Амплитуда и частота этих колебаний меняются при изменении скорости вращения двигателя, что достигается с помощью реостата 9.  К нижней части стола с помощью кронштейна прикреплен динамометр, другой конец которого связан с ходовым винтом, установленным на неподвижном основании установки. При вращении ходового винта на стол действует сила, которая деформирует пружины стола. Замерив перемещение и отсчитав по динамометру силу, можно определить жесткость системы на перемещение стола в горизонтальном направлении.

Экспериментальная часть.

Определение жесткости пружин стола:

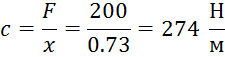
F – показания динамометра в Н;

Для определения жесткости пружин стола мы несколько раз натягивали пружину динамометра  до нагрузки в 200 Н и записывали показания микрометра в метрах. После этого мы вычислили истинное значение жесткости пружин (приняв за него среднеарифметическое значение вычислений)  по указанной выше формуле.

 Определение декремента и частоты свободных колебаний.

Включив записывающее устройство и сообщив столу от руки начальный импульс, мы получили запись свободных затухающих колебаний. 

По виброграмме мы  определили:

-Период колебаний

-фактор затухания

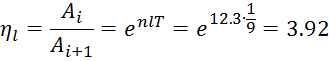
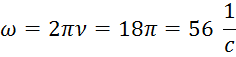
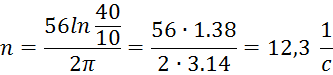
-логарифмический  декремент колебаний

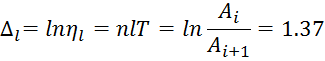
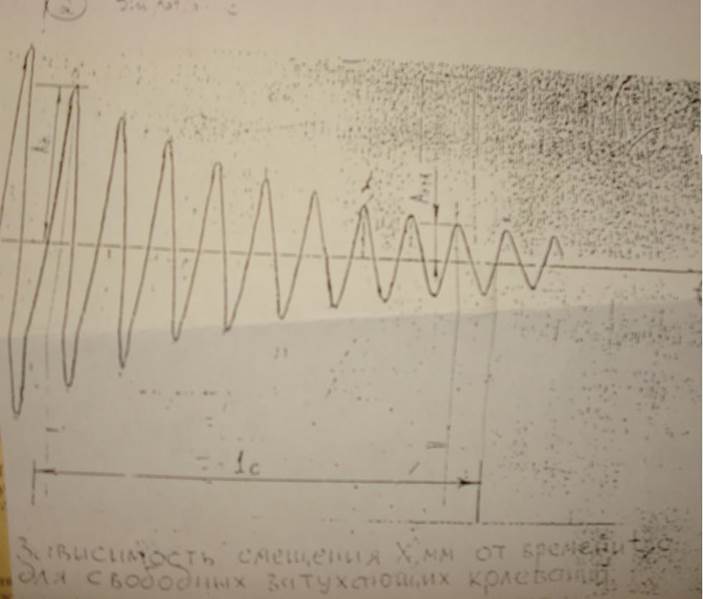
(Рис 2.) Зависимость смещения X, мм от времени t ,с для свободных затухающих колебаний.

Определение массы стола:

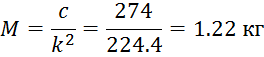
k – собственная частота системы (1/с);

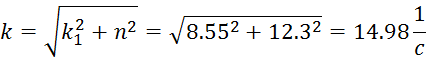
Таблица 1.

ω, Гц	Деления	Масштаб	Вычисления
3,93	0,5	0,05	0,025
5,17	1	0,05	0,05
6,04	2	0,05	0,1
6,94	2,5	0,05	0,125
8,21	10	0,2	2
8,54	16	0,2	3,2
8,89	17	0,2	3,4
10,37	6	0,1	0,6
11,11	5	0,1	0,5
12,14	4	0,1	0,4

Амплитудно-частотная характеристика для системы без гасителя.

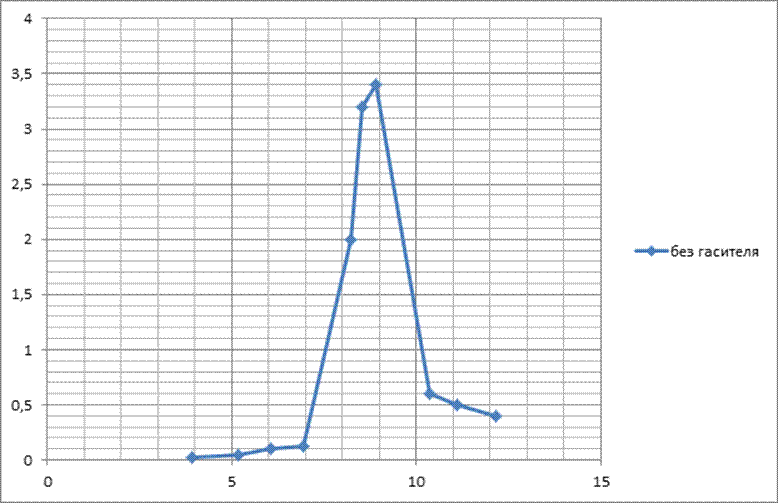
(Рис 3.)

Таблица 2.

ω, Гц	Деления	Масштаб	Вычисления
5,18	1	0,05	0,05
6,18	2	0,05	0,1
7,02	3	0,05	0,15
7,92	12	0,2	2,4
9,26	0	0,2	0
10,04	11	0,2	2,2
10,85	6,5	0,1	0,65
12,03	4	0,1	0,4

Амплитудно-частотная характеристика для системы с гасителем.

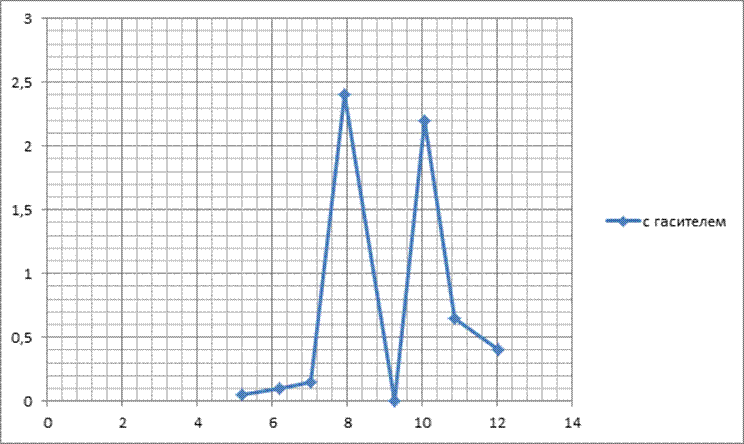
(Рис 4.)

Наложим друг на друга графики  для системы с гасителем и без:

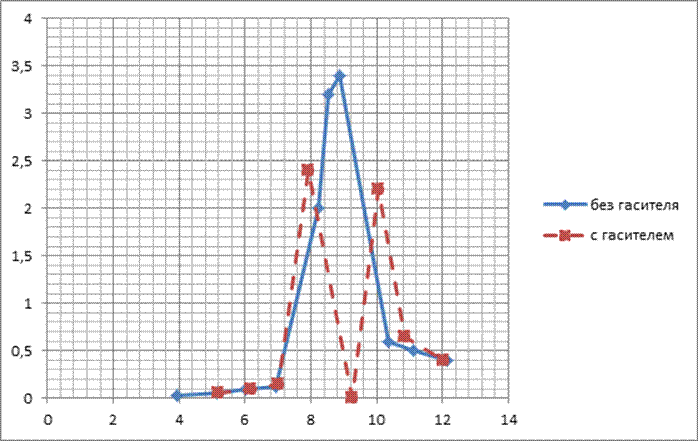
(Рис 5.)

Из графиков видно, что резонанс для системы с одной степенью свободы наблюдаемся при частоте ω = 8,89 Гц, а для системы с двумя степенями свободы  наблюдается два резонанса при частотах  ω=7,92 Гц  и ω =10,04 Гц однако значение амплитуды для системы с двумя степенями свободы оказалось  меньше.

Теоретический расчет свободных и вынужденных колебаний системы с одной степенью свободы (вибрационный стол без динамического гасителя).

Расчетная схема установки (Рис6):

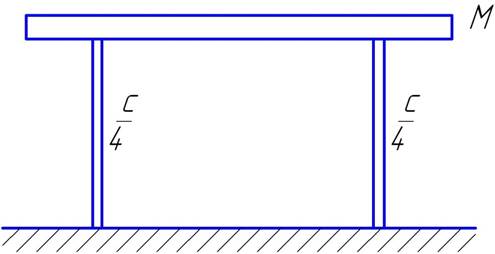
(Рис 6.)

М – масса системы ( стол, двигатель);

с – жесткость системы на перемещение стола в горизонтальном продольном направлении;

Уравнение, описывающее движение системы:

 

Теоретический расчет свободных и вынужденных колебаний системы с двумя степенями свободы (вибрационный стол с динамическим гасителем колебаний)

Расчетная схема установки  (Рис 7.):

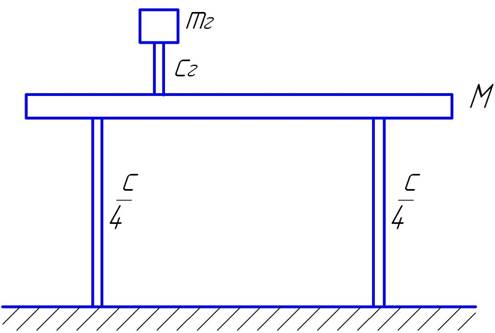
(Рис 7.)

m_г – масса груза динамического гасителя колебаний;

c_г – жесткость пружины гасителя на перемещение массы в горизонтальном направлении, совпадающем с продольной осью стола;

Уравнения описывающее движение системы:

Вывод:

При экспериментальном исследовании системы с одной степень свободы наблюдался резонанс при частоте 8,89 Гц, амплитуда была равна 3,4. При дальнейшем исследовании системы с двумя степенями свободы наблюдались два резонанса, при 7,92 Гц – 2,4 и 10,04 Гц – 2,2  соответственно. При этом, исходя из АЧХ можно сказать, что резонанс  в системе с одной степень свободы «распался» на два резонанса в системе с двумя степенями свободы, резонансы достигали меньших значений амплитуд, что тоже важно. Таким образом, можно сделать вывод, что использование динамического гасителя колебаний позволяет существенно снизить интенсивность колебаний различных сооружений, деталей, что увеличивает их долговечность и снижает вероятность выйти из строя, сломаться

Литература:

1.  Ю.А. Иовлев, В.И. Осорин  “Лабораторные работы по курсу теории колебаний”.

2.  Я.Г. Пановко “Основы прикладной теории упругих колебаний”.