Первый закон Кирхгоффа

Задача №8. В электрической цепи, изображенной на рис., известны ЭДС источника и споротивления резисторов. Найти токи во всех ветвях цепи.

 

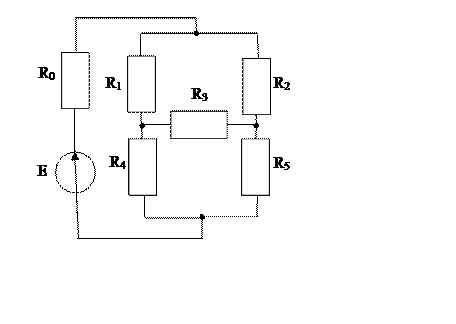Вариант	E, B	R0, Ом	R1, Ом	R2, Ом	R3, Ом	R4, Ом	R5, Ом
1	20	1	2	3	1	8	5

Решение:

1.  Заменим соединение треугольником резисторов R1, R2, R3 на эквивалентное соединение звездой резисторов R₁₂, R₁₃, R₂₃.

 

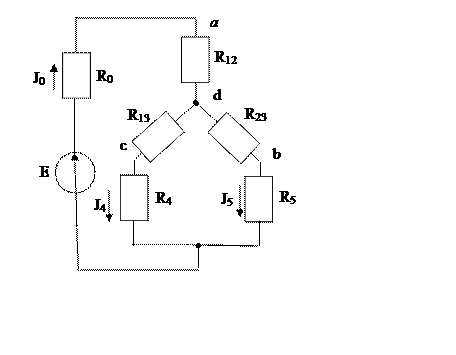При этом применим формулы, стандартные для перехода от соединения типа «звезда» (или «Т») к соединению типа «треугольник» (или «П»).

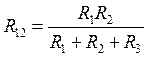=(2*3)/(2+3+1)=1 Ом

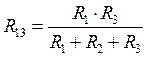=(2*1)/(2+3+1)=1/3 = 0.33 Ом

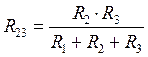=3/6=1/2 = 0.5 Ом

2.  Сопротивление эквивалентное соединению резисторов R13, R23, R4 и R5 определится:

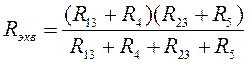= (1/3+8)*(1/2+5)/(1/3+8+1/2+5)=3.31 Ом

3.  Сопротивление всей цепи определится:

 = 1+1+3,313=5.31 Ом

=20/5.31 =3.77 А

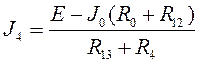=(20-3.77*(1+1))/(1/3+8)=1.50 А

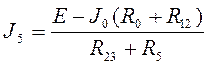=(20-3.77*(1+1))/(1/2+5)=2.27 А

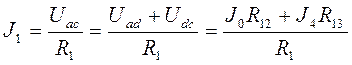=(3.77*1+1.50*1/3)/2=2.13 А

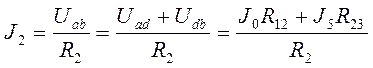=(3.77+2.27*1/2)/3=1.64 А

Токи J₁ и J₂ направлены в ту же сторону, что и токи J4 и J5, т.е. вниз.

4.  Ток J₃ найдем из первого закона Кирхгоффа, который является следствием закона сохранения заряда и  гласит: алгебраическая сумма токов в узле электрической цепи равна 0. В нашем случае для узла, в котором сходятся ветки цепи с резисторами R1, R3 и R4, ток J₁ является входящим (мы предполагаем, что он направлен вниз), ток J₄ является выходящим (предполагается, что он направлен вниз), ток J₃ является входящим (предполагаем, что он направлен влево). Обычно входящий в узел ток берут со знаком «+», а выходящий со знаком «-».

Первый закон Кирхгоффа запишется так:

J1-J4+J3=0,

Откуда следует, что = 1.50-2.13=-0.63 А .

Поскольку ответ получился отрицательный, то ток J₃  направлен вправо.

Ответ:

Задача 13. В схеме на рис. Известны напряжение U на входе, активная мощность P, потребляемая цепью, частота тока f. В неразветвленной части цепи ток при разомкнутом ключе S равен I₁, а при замкнутом ключе I₂. Рассчитать сопротивление резистора R, индуктивность катушки L и емкость конденсатора C.

Вариант	U, B	P, Вт	f, Гц	I1, А	I2, А
1	100	200	50	5	3

Решение:

При разомкнутом ключе:

1 . Если ключ разомкнут, то то можно не рассматривать ту часть цепи, где находится ключ. Поскольку активная мощность – есть мощность, которая выделяется на резисторе (приводит к его нагреванию) и вычисляется по формуле , (где JR – ток через резистор), то сопротивление резистора всегда можно найти, зная мощность, которая на нем выделяется.

В нашем случае речь идет об активной мощности, которая потребляется всей цепью, а значит, выделяется на всех резисторах цепи. Как видно по схеме, резистор только один, поэтому:

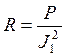= 8 Ом.

2. Найдем комплексное сопротивление:

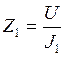= 20 Ом.

Комплексное сопротивление всегда состоит из суммы 2-х частей: активного сопротивления, к которому относится сопротивление резистора или группы резисторов, и реактивного сопротивления, к которому относятся сопротивление катушки индуктивности и сопротивление конденсатора.

, где

R – активное сопротивление, X – реактивное сопротивление, j – мнимая единица.

3. Запись комплексного сопротивления в виде геометрически представляет собой прямоугольный треугольник с гипотенузой длины Z и катетами длины R и Х (обычно R располагают горизонтально, а X - вертикально). Поэтому всегда, зная какие-нибудь 2 величины из 3-х (Z,R,X) можно найти третью, используя теорему Пифагора.

Найдем реактивное сопротивление:

=18.33 Ом

Поскольку в данном случае реактивная составляющая связана с наличием катушки индуктивности, то сопротивление катушки находится по формуле:

где f – частота, Гц,  L - индуктивность, Гн.

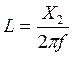=5.8*10⁴ мкГн

4. Запишем комплексное сопротивление в экспоненциальной форме, которая удобна при вычислениях умножения и деления. Переход из одной форму в другую осуществляется так:

Пусть есть число . Надо записать его в виде , где e- экспонента или основание натуральных логарифмов.

Z₀ не что иное как величина гипотенузы прямоугольного треугольника с катетами R и X. Находим по Теореме Пифагора:

Z₀ также называют модулем или абсолютной величиной комплексного сопротивления.

 – это угол, тангенс которого считается как отношение X/R (то есть угол между гипотенузой и активной составляющей сопротивления, в нашем случае обозначенной через