Методы и модели в экономике. Оптимальное распределение ресурсов. Транспортная задача

ряда шагов, состоящих в том, что от данного базиса  переходим к другому базису  с таким расчетом, чтобы значение целевой функции F увеличивалось, или, по крайней мере не уменьшалось, т.е. .

Геометрическая интерпретация симплекс-метода состоит в том, что аналитическому переходу от одного базиса к другому соответствует переход от одной вершины многоугольника множества допустимых решений к другой, в которой целевая функция имеет не меньшее значение. Этот факт основан на том, что вершинам многоугольника множества допустимых решений соответствуют опорные решения системы ограничений.

Решение симплекс-методом заканчивается, когда среди опорных решений будет найдено такое, которое обеспечивает максимум линейной формы (1.3). Такое решение называется оптимальным.

РЕАЛИЗАЦИЯ СИМПЛЕКС-МЕТОДА

Рассмотрим идею симплекс-метода на конкретном примере

  (1.21)

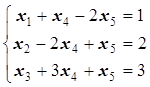     (1.22)

                (1.23)

Решение. Данная система уравнений ограничений совместна, так как ранги матрицы системы

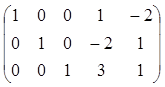
и расширенной системы

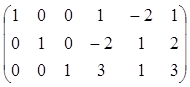
совпадают и равны 3. Следовательно, три переменные (базисные) можно линейно выразить через две свободные переменные. Выразим, например, x₁, x₂ и x₃через x₄ и x₅, т.е. приведем систему к единичному базису:

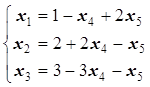                                                (1.21)

Линейная форма  уже выражена через x₄ и x₅.

При x₄ =0 и x₅=0, найдем значение базисных переменных x₁=1, x₂=2 и x₃=3.

Таким образом, первое допустимое решение имеет вид x₁=1, x₂=2 , x₃=3, x₄ =0 , x₅=0 или (1,2,3,0,0). При найденном допустимом решении линейная форма F имеет значение 0, т.е. F₁=0.

Теперь попытаемся увеличить значение F:

-  увеличение x₄уменьшит F , так как перед x₄стоит отрицательный коэффициент, а увеличение x₅ даст увеличение и F₁;

-  будем  увеличивать x₅  таким образом, чтобы одна из базисных переменных (x₁ илиx₂или x₃) обратилась в ноль, а остальные базисные переменные оставались бы неотрицательными.

Анализируя первое уравнение системы (1.21) приходим к выводу, что x₅ можно увеличить неограниченно. При этом x₁ остается положительным и никогда не обратиться в ноль. Из второго уравнения системы (1.21) следует, что x₅ можно увеличить до 2 (больше увеличивать нельзя, т.к. x₂ станет отрицательным). Из третьего уравнения системы (1.21) следует, что x₅ можно увеличить до 3. Принимая во внимание приведенный анализ, приходим к выводу, что x₅=2.

Таким образом, получим второе допустимое решение x₁=5, x₂=0 , x₃=1, x₄ =0 , x₅=5 или (5,0,1,0,2).

Значение линейной формы F  при этом допустимом решении равно F₂=2, т.е. значение целевой функции увеличилось.

Примем за свободные переменные x₂ и x₄., т.е. те переменные, которые в этом решение равны 0. С этой целью из второго уравнения системы (1.21) выразим x₅  Получим. Тогда

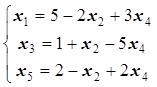 (1.22)

Для увеличения значения F будем увеличивать x₄. Проведя аналогичный анализ системы (1.22), заключаем, что, что x₄ можно увеличить до 1/5. (Следует из рассмотрения  второго уравнения системы (1.22)). Таким образом, получим третье допустимое решение x₁=28/5, x₂=0 , x₃=0, x₄ =1/5 , x₅=12/5 или (28/5,0,0, 1/5, 12/5). Значение линейной формы F  при этом допустимом решении равно F₃=11/5, т.е. значение целевой функции увеличилось.

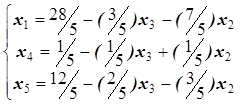 (1.23)

Так как в последней линейной форме обе свободные переменные входят с отрицательными коэффициентами, то наибольшее значение достигается при x₂=0 , x₃=0.

Из этого следует, что решение (28/5,0,0, 1/5, 12/5) является оптимальным и F_max=11/5.

Для того, чтобы упростить трудоемкие операции по пересчету коэффициентов и  перезаписи системы ограничений, можно выполнять преобразования специальной симплекс-таблицы.

Симплексные таблицы

Для составления этой таблицы систему фазовых ограничений и целевую функцию необходимо записать в стандартной форме, т.е. сведенной к единичному базису:

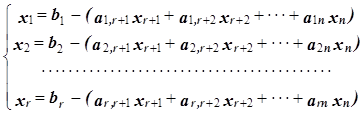 (1.24)

  (1.25)

В виде таблицы эти данные можно представить так:

Таблица 1.1

Базисные  переменные		…		…			…		…		Свободные члены
	1	…	0	…	0				…
…	0	…	0	…	0	…		…	…	…	…
	0	…	1	…	0				…
…	…	…	…	…	…	…	…	…	…	…	….
	0	…	0	…	1				…
F	0	…	0	…	0				…

Заметим, что в строку с целевой функцией коэффициенты записываются с противоположным знаком .

Каждой итерации соответствует преобразование симплексной таблицы, в результате которого получается новое базисное решение, которому соответствует первый столбец.

Правила преобразования симплексной таблицы.

1. Выбирают разрешающий столбец из условия  и хотя бы один элемент .

2. Выбирают q-ю разрешающую строку из условия

Элемент , стоящий на пересечении разрешающего ( с индексом p) столбца и разрешающей ( с индексом q) строки, называется разрешающим элементом.

3. В состав базисных переменных вводят , её записывают в строку с номером q.

4. Производят пересчет элементов разрешающей q-й строки по формуле

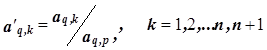
В результате преобразования получают единицу на месте разрешающего элемента.

5. Вычисляют элементы всех остальных строк  (при k¹p) по формуле:

Строке с номером r+1 соответствует строка целевой функции, столбцу с номером n+1 соответствует столбец свободных членов.

Другими словами, умножая  разрешающую строку на подходящие числа и прибавляя ее к остальным строкам, добиваются, чтобы остальные элементы разрешающего столбца стали равными нулю.

6. Далее анализируем полученную таблицу. Если решение получено или выяснено, что его нет, процесс решения закончен. Иначе переходим к пункту 1.

Анализ базируется на основной теореме симплекс-метода.

ТЕОРЕМА

Если после выполнения очередной итерации (преобразования):

1)  найдется хотя бы один отрицательный коэффициент  и в каждом столбце с таким коэффициентом окажется хотя бы один положительный элемент, то можно улучшить решение, выполнив следующую итерацию;

2)  найдется хотя бы один отрицательный коэффициент  и в соответствующем столбце не содержится положительных элементов, то функция F не ограничена в области допустимых решений;

3)  все коэффициенты окажутся неотрицательными, то оптимальное решение достигнуто.

Рассмотрим решение той же задачи (1.21)-(1.23) с помощью симплекс таблиц.

Исходная симплекс таблица, определяемая соотношениями (1.21)-(1.23) показана на рис.(1.5).

Рис.1.5. Исходная симплекс таблица.

Заметим, что целевая функция в данном примере может быть записана в виде , что соответствует виду (1.25). В качестве разрешающего столбца выберем столбец соответствующий x₅ , поскольку в нем  в строке с целевой функцией стоит отрицательный элемент (-1).

Для определения разрешающей строки заполним вспомогательный столбец (рис.1.6)

Первая клетка в этом столбце оставлена пустой, поскольку в соответствующей клетке столбца x₅ , стоит отрицательный элемент (-2).

Из этого столбца выбираем минимальное значение min{2;3}=2, это значение стоит во второй строке, поэтому берем её в качестве разрешающей.

Рис.1.6. Выбор разрешающего столбца и разрешающей строки для первой итерации.

Выполним преобразования указанные в п.п.4-5 для табл.1.1. Результат приведен на рис.1.7. Значение целевой функции F=2.

Рис.1.7. Симплекс таблица после первой итерации.

Поскольку в строке, соответствующей целевой функции, имеется отрицательный элемент –1 (столбец x₄), необходимо выполнить еще одну итерацию.

Для определения разрешающей строки (разрешающий столбец уже очевиден -  x₄) заполним таблицу рис.1.8.

Рис.1.8. Выбор разрешающего столбца и разрешающей строки для второй итерации.

Выбор разрешающей строки свелся к выбору из одной строки, поскольку только в строке x₃ стоит положительный элемент. Выполним преобразования указанные в п.п.4-5 для таблицы рис.1.7, результат в таблице на рис. 1.9.

Рис.1.9. Симплекс таблица после второй итерации.

В строке, соответствующей целевой функции, нет отрицательных элементов, следовательно, получено оптимальное решение (28/5,0,0, 1/5, 12/5) и F_max=11/5. Заметим, что решения совпали.

2. ЗАДАЧА ОБ ОПТИМАЛЬНОМ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ

Если финансы, оборудование, сырье и даже людей полагать ресурсами, то значительное число задач в экономике можно рассматривать как задачи распределения ресурсов. Достаточно часто математической моделью таких задач является задача линейного программирования, которая записывается следующим образом:

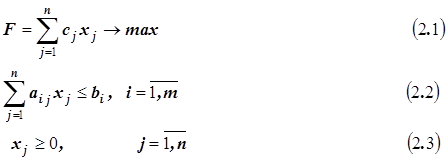
Здесь (2.1) - целевая функция; (2.2) - система ограничений; (2.3) - естественные граничные условия;

x_j– количество выпускаемой продукции j-го типа, j=1,2, …n;

b_i - количество располагаемого ресурса i-го вида, i=12,….,m;

a_ij- норма расхода i-го ресурса для выпуска единицы продукции j-го типа;

c_j- прибыль, получаемая от реализации единицы продукции j-го типа.

В этом случае значение целевой функции - это суммарная величина прибыли от реализации продукции, выпущенной в объемах x₁,x₂,...x_n. Левая часть неравенства (2.2) представляет собой общее количество ресурса i, используемое в соответствии с планом, правая часть -  это имеющийся запас.

Эта задача является частным случаем общей задачи линейного программирования, теория применения которого была изучена в курсе Высшей математики [5]. Основными положениями этой теории являются следующие положения:

Каждой задаче линейного программирования соответствует двойственная задача, которая записывается по следующим правилам:

1.  Каждому i-му ограничению исходной задачи соответствует переменная двойственной задачи z_i(двойственная переменная)

2.  Каждой j-ой переменной исходной задачи соответствует ограничение двойственной. Матрица коэффициентов ограничений двойственной задачи является транспонированной матрицей ограничений исходной. Если в исходной задаче ограничения имеют знак £, то в двойственной - ³

3.  Коэффициенты при двойственных переменных в целевой функции двойственной задачи равны правым частям ограничений исходной задачи

4.  Если исходная задача была на нахождение максимума, то двойственная будет на нахождение минимума:

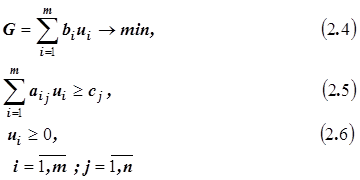
§  Для оптимального решения значения целевых функций прямой и двойственной задач совпадают (maxF=minG).

§  Если это записать в форме 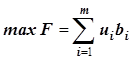, то видно, что двойственная переменная u_iявляется коэффициентом при b_i и, следовательно, показывает, как изменится целевая функция при изменении ресурса b_i на единицу. В литературе по оптимизации двойственные переменные принято называть двойственными оценками. В отчетах Excel двойственная оценка называется теневой ценой.

§  Теневая цена ресурса отлична от нуля (точнее больше нуля) только для тех видов ресурсов, которые используются полностью, т.е. ограничения (2.2) превращаются в равенства.

Принцип дополняющей полужесткости !!!!!!

§  Симметричность прямой и двойственной задач заключается