Основы информационных технологий и программирование

регрессионная таблица должна содержать пять строк и по одному столбцу на каждый коэффициент. В случае линейного приближения ширина таблицы равна двум.

Перейдем к вычислению коэффициентов.

Выделим ячейки F8:G12 и введите формулу

=ЛИНЕЙН(B3:B11;A3:A11;ИСТИНА;ИСТИНА)

Поскольку функция возвращает массив, она должна задаваться в виде формулы массива при помощи комбинации клавиш <Ctrl> + <Shift> + <Enter>.

Так как функция возвращает дополнительную регрессию по статистике, то отдельно выполнять расчет для регрессионной и остаточной сумм квадратов нет необходимости.

·  построить в одной системе координат точечный график заданной функции y=f(x) и линейной аппроксимирующей функции y=F(x)

3. Найти коэффициенты линейной аппроксимирующей функции y=F(x) для функции y=f(x), которая задана таблицей (Табл.11.1) с использованием надстройки Поиск решения

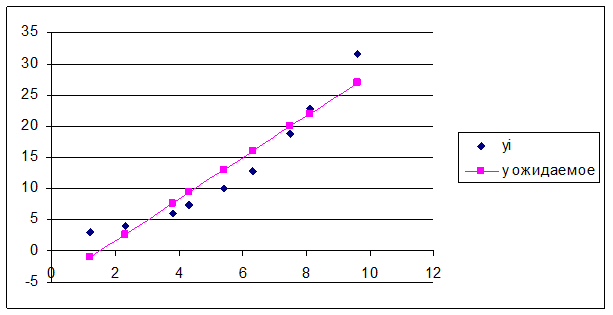
·  найти регрессионную сумму квадратов

·  найти остаточную сумму квадратов

·  найти коэффициент детерминированности

В ячейки  А3:А11 вводим заданные значения x_i , в ячейки  В3:В11 вводим заданные значения y_i.. Пусть в ячейках F3 и F4 находятся искомые коэффициенты аппроксимирующей функции. В качестве начального приближения можно выбрать любые значения, например, 0. В ячейку С3 вводим =$F$4*A3+$F$3, скопируем формулу в ячейки С4:С11.

В ячейку F8 вводим формулу для r²

=1-СУММ((B3:B11-C3:C11)^2)/СУММ((B3:B11-СРЗНАЧ(B3:B11))^2)

В ячейку F9 вводим формулу для регрессионной суммы квадратов

=СУММ((B3:B11-СРЗНАЧ(B3:B11))^2)

В ячейку F10 вводим формулу для остаточной суммы квадратов

=СУММ((B3:B11-C3:C11)^2)

Для того, чтобы формулы воспринимались как формулы массива, необходимо при вводе каждой из них нажимать комбинацию клавиш <Ctrl> + <Shift> + <Enter>.

Установим табличный курсор в ячейку F8 и выполним команду меню Сервис → Поиск решения. Заполним диалоговое окно как показано на рисунке.

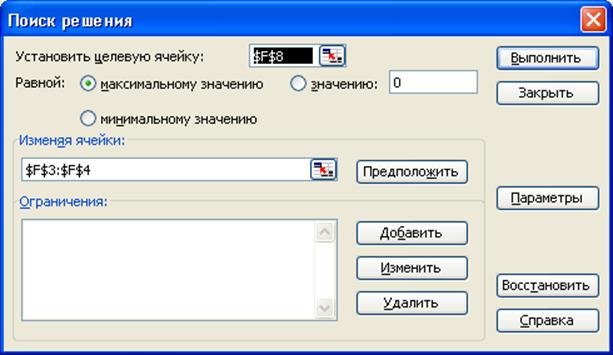
Нажмем кнопку "Выполнить".

·  построить в одной системе координат точечный график заданной функции y=f(x) и линейной аппроксимирующей функции y=F(x)

4. Найти коэффициенты квадратичной аппроксимирующей функции y=F(x) для функции y=f(x), которая задана таблицей (Табл.11.1) решением системы линейных алгебраических уравнений

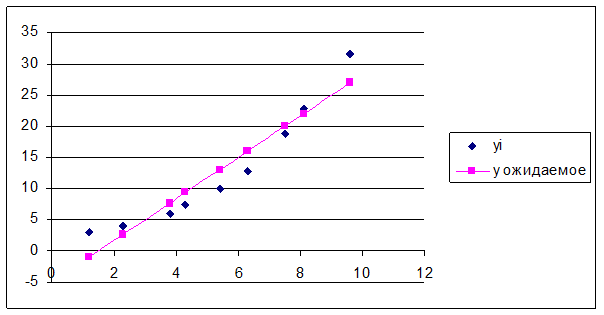
Аппроксимирующая квадратичная функция имеет вид y=сx²+bx+a. Для нахождения неизвестных коэффициентов A и B необходимо решить следующую систему уравнений:

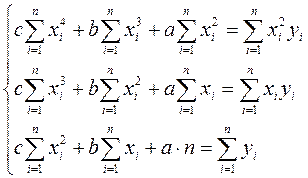
Составим таблицу для вычисления коэффициентов СЛАУ:

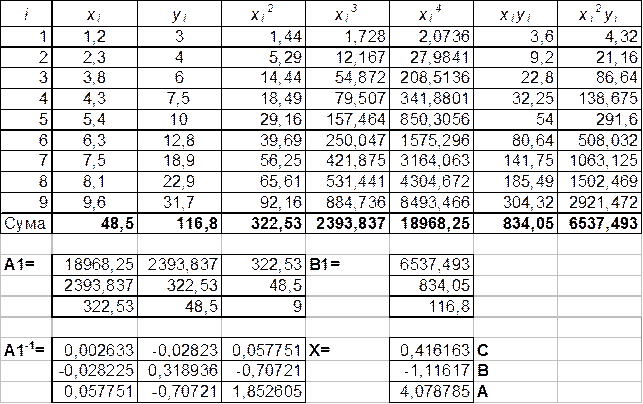
Получим матрицу коэффициентов системы уравнений A1 и столбец правых частей уравнений B1.

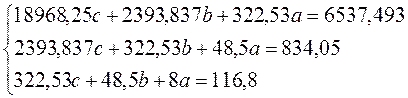
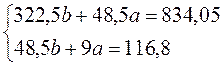
Решение данной системы находится из следующего соотношения , где А1 – матрица коэффициентов системы, В1 – вектор правой части.

Используя матричные функции Excel, получим

X={0,4161163;-1,11617;4,078785}.

Таким образом, аппроксимирующая функция имеет вид .

·  найти регрессионную сумму квадратов

·  найти остаточную сумму квадратов

·  найти коэффициент детерминированности

·  построить в одной системе координат точечный график заданной функции y=f(x) и квадратичной аппроксимирующей функции y=F(x)

5. Найти коэффициенты квадратичной аппроксимирующей функции y=F(x) для функции y=f(x), которая задана таблицей (Табл.11.1) вычислением степенной регрессии с помощью функций Excel.

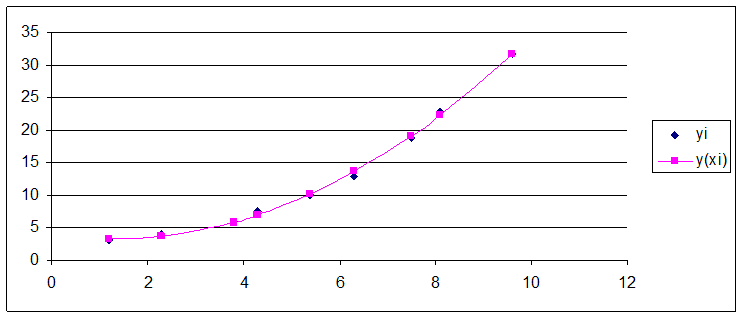
·  найти регрессионную сумму квадратов

·  найти остаточную сумму квадратов

·  найти коэффициент детерминированности

Заполненный рабочий лист Excel с введенными данными и выполненными расчетами приведен на рисунке ниже.

В ячейки А3:А11 вводим заданные значения x_i , в ячейки В3:В11 вводим подсчитанные значения x_і², в ячейки С3:С11 вводим заданные значения y_i..

Для удобства присваиваем ячейкам G8, H8, I8 имена С_к, В_к, А_к соответственно.

В ячейку D3 вводим =С_к*A3^2+В_к*A3+А_к, скопируем формулу в ячейки D4:D11.

Перейдем к вычислению коэффициентов.

Выделим ячейки G8:І12 и вводим формулу

=ЛИНЕЙН(С3:С11;А3:В11;ИСТИНА;ИСТИНА)

Поскольку функция возвращает массив, она должна задаваться в виде формулы массива при помощи комбинации клавиш <Ctrl> + <Shift> + <Enter