Суммарные запасы и суммарные потребности не совпадают

Задание 2

Имеется четыре карьера, производящих строительные материалы, и четыре потребителя сырья строительных материалов. Известны объемы производства на каждом карьере, потребности в их продукции каждого из потребителей, а также стоимость перевозки одной тонны продукции I-го карьера а J-му потребителю. Определить При какие объемах грузоперевозок от I-го поставщика к J-му потребителю суммарная стоимость перевозок будет минимальной.

1.  Решить задачу посредствам Excel (Надстройка «Поиск решения»).

2.  Решить задачу аналитически.

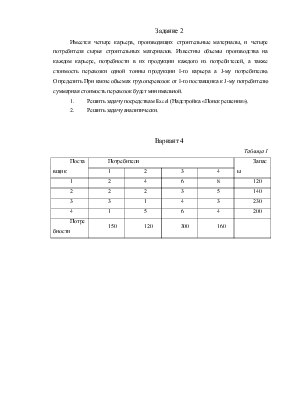
Вариант 4

Таблица 1

Решение.

1. Решение методом потенциалов

Построим математическую модель данной задачи

Вычислим суммарные запасы:

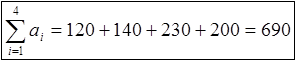и суммарные потребности:

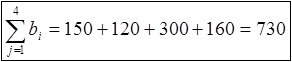Суммарные запасы и суммарные потребности не совпадают => это задача открытого типа.

Данная задача решается введением фиктивного поставщика.

Стоимость всех фиктивных перевозок равна нулю.

Построим опорное решение методом «северо-западного» угла (таблица 2)

Таблица 2

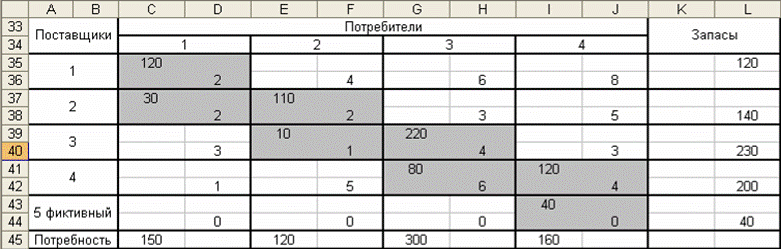
Суммарная стоимость перевозок равна:

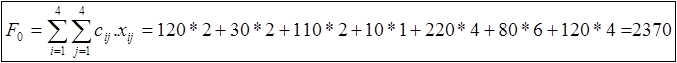Рассчитаем систему потенциалов для этого решения.

Для определения U₁, U₂, U₃, U₄, V₁, V₂, V₃, V₄ имеем следующую систему уравнений:

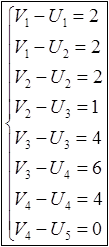                        Имеем 8 уравнений и 9 неизвестных.

Положим что U₁=0, тогда остальные величины будут равны:

V₁=2,

V₂=2

V₃=5

V₄=3

U₂=0

U₃=1

U₄=-1

U₅=3

Припишем значения потенциалов соответствующим строкам и столбцам (таблица 3).

Введем дополнительный столбец U_i и дополнительную строку V_j и занесем вычисленные значения потенциалов в полученные клетки

Таблица 3

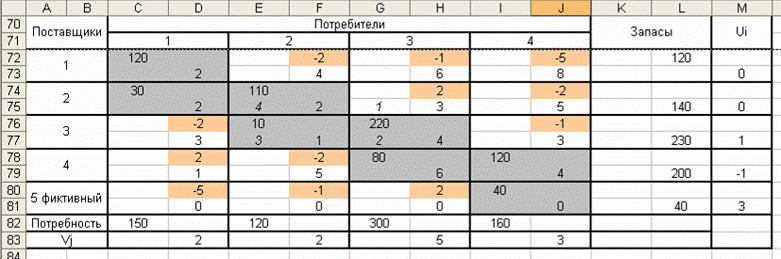
Вычислим значения невязок для всех клеток без перевозок по формуле:

В ряде клеток (2,3) и (4,1) наблюдаются нарушения  (невязка больше нуля)

Выберем клетку (2,3) в которой превышение равно 2.

Построим замкнутый цикл с началом в этой точке.

В качестве остальных вершин выберем клетки (3,3), (3,2), (2,2)

Нечетные вершины (2,3), (3,2) образуют положительную полуцепь.

Четные вершины (3,3), (2,2) образуют отрицательную полуцепь.

Величина q=min{110;220}=110

Вычислим новые значения для узлов контура. В четных вершинах значения уменьшаются на 110, в клетке (2,2) значение станет равным 110-q=0

в клетке (3,3) - равным 220-q=220-110=110

В нечетных вершинах значение увеличивается на q=110, так в клетке (2,3) значение равно 0+q=0+110=110

а в клетке (3,2) значение равно 10+q=10+110=120

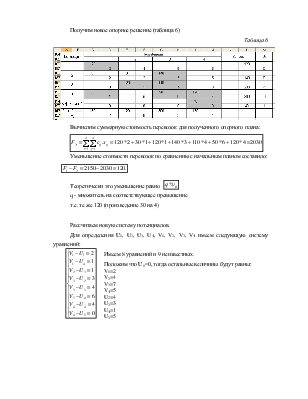
Получим новое опорное решение (таблица 4)

Таблица 4

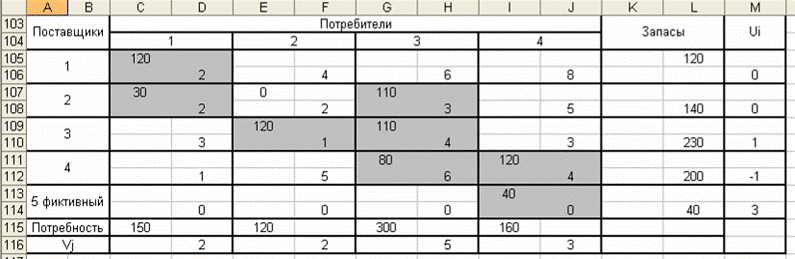
Вычислим суммарную стоимость перевозок для полученного опорного плана:

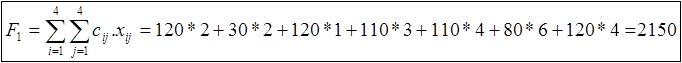Уменьшение стоимости перевозок по сравнению с начальным планом составило:

Теоретически это уменьшение равно

q - множитель на соответствующее превышение т.е. те же 220 (произведение 110 на 2)

Рассчитаем новую систему потенциалов.

Для определения U₁, U₂, U₃, U₄, V₁, V₂, V₃, V₄ имеем следующую систему уравнений:

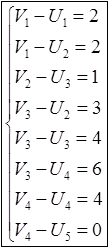                        Имеем 8 уравнений и 9 неизвестных.

Положим что U₁=0, тогда остальные величины будут равны:

V₁=2

V₂=0

V₃=3

V₄=1

U₂=0

U₃=-1

U₄=-3

U₅=1

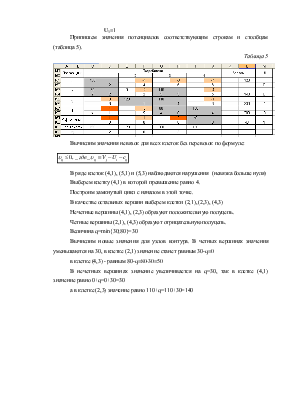
Припишем значения потенциалов соответствующим строкам и столбцам (таблица 5).

Таблица 5

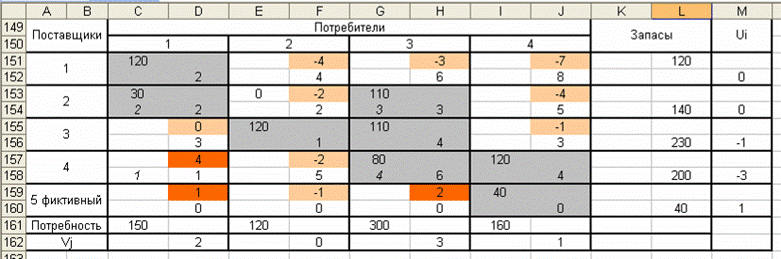
Вычислим значения невязок для всех клеток без перевозок по формуле:

В ряде клеток (4,1), (5,1) и (5,3) наблюдаются нарушения  (невязка больше нуля)

Выберем клетку (4,1) в которой превышение равно 4.

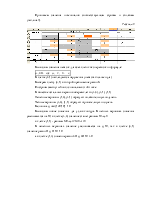
Построим замкнутый цикл с началом в этой точке.

В качестве остальных вершин выберем клетки (2,1), (2,3), (4,3)

Нечетные вершины (4,1), (2,3) образуют положительную полуцепь.

Четные вершины (2,1), (4,3) образуют отрицательную полуцепь.

Величина q=min{30;80}=30