Порядок (или
степень Whitney(Уитни) элементов (УЭ)) определяется не
порядком представляющих их полиномов, а «степенью (порядком)» симплекса,
ассоциированного с этим элементом. Введем УЭ, ассоциированные с ребром, гранью
и тетраэдром, и обозначим их соответственно: ![]() ,
, ![]() и
и ![]() . Введем
обозначения:
. Введем
обозначения: ![]() - ограниченная область трехмерного
пространства (
- ограниченная область трехмерного
пространства (![]() ), с кусочно-гладкой границей
), с кусочно-гладкой границей ![]() ;
; ![]() разбита
на тетраэдры (тетраэдральная сетка), которые, по принципу соседства, имеют либо
общую грань, либо общее ребро, либо общий узел. Обозначим
разбита
на тетраэдры (тетраэдральная сетка), которые, по принципу соседства, имеют либо
общую грань, либо общее ребро, либо общий узел. Обозначим ![]() ,
, ![]() ,
, ![]() ,
, ![]() - узлы,
ребра, грани, тетраэдры соответственно, т.е. множество симплексов,
размерности 0, 1, 2, 3, полученные на сетке m.
Кроме списка узлов и их позиций сеточная структура данных содержит матрицу
инциденций, определяющую: какой узел принадлежит какому ребру, и какое
ребро принадлежит какой грани, и какая грань принадлежит какому тетраэдру.
Кроме того, мы имеем представление об ориентации симплексов, которые играют
какую-то роль. Короче, ребра, грани и т.д. есть не только двухузловые,
трехузловые и т.д. подмножества множества
- узлы,
ребра, грани, тетраэдры соответственно, т.е. множество симплексов,
размерности 0, 1, 2, 3, полученные на сетке m.
Кроме списка узлов и их позиций сеточная структура данных содержит матрицу
инциденций, определяющую: какой узел принадлежит какому ребру, и какое
ребро принадлежит какой грани, и какая грань принадлежит какому тетраэдру.
Кроме того, мы имеем представление об ориентации симплексов, которые играют
какую-то роль. Короче, ребра, грани и т.д. есть не только двухузловые,
трехузловые и т.д. подмножества множества ![]() , но
также множество ориентаций симплексов относительно друг друга (учет того, что
они «собираются» (стягиваются)).
, но
также множество ориентаций симплексов относительно друг друга (учет того, что
они «собираются» (стягиваются)).
Отметим, что
если симплекс ![]() принадлежит сетке, то все
симплексы, которые формируют границу
принадлежит сетке, то все
симплексы, которые формируют границу ![]() , также принадлежат ей.
Кроме того, каждый симплекс появляется только однажды. Такая структура
называется симплициальный комплекс.
, также принадлежат ей.
Кроме того, каждый симплекс появляется только однажды. Такая структура
называется симплициальный комплекс.
Ориентированные симплексы
1) Ребра
![]()
![]()
Ребро ![]() ориентировано от
ориентировано от ![]() к
к
![]() . Все ребра сетки ориентированы принадлежат
множеству
. Все ребра сетки ориентированы принадлежат
множеству ![]() .
.
Определим «числа
инциденций»: ![]() , если
, если ![]() не
совпадает с
не
совпадает с ![]() или
или ![]() . В
результате получим некоторую матрицу
. В
результате получим некоторую матрицу ![]() с
с ![]() столбцами и
столбцами и ![]() строками,
которая описывает как ребра соединяются с узлами.
строками,
которая описывает как ребра соединяются с узлами.
2) Грани
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Грани
ориентированы и принято подобное же соглашение: дан список узлов и их
ориентация. Грань ![]() имеет три вершины, узлы
имеет три вершины, узлы ![]() и
и ![]() ,
которые можно «переставлять»:
,
которые можно «переставлять»: ![]() ,
, ![]() , и они все равно являются узлами грани
, и они все равно являются узлами грани ![]() , но определяют четную перестановку;
или нечетную перестановку, которую определим как противоположно
ориентированную грань, которая не принадлежит
, но определяют четную перестановку;
или нечетную перестановку, которую определим как противоположно
ориентированную грань, которая не принадлежит ![]() , если
грань
, если
грань ![]() задана. Общепринято: положительно и
отрицательно ориентированная система координат («правое» или «левое» вращения).
Ориентация грани
задана. Общепринято: положительно и
отрицательно ориентированная система координат («правое» или «левое» вращения).
Ориентация грани ![]() обусловливает ориентацию её
границ: тангенциальный вектор
обусловливает ориентацию её
границ: тангенциальный вектор ![]() вдоль границы
положительно ориентирован, если
вдоль границы
положительно ориентирован, если ![]() есть прямая система
координат, где
есть прямая система
координат, где ![]() - «внешненаправленный вектор» в
плоскости
- «внешненаправленный вектор» в
плоскости ![]() относительно
относительно ![]() .
.
Вновь
определим «число инциденций»: ![]() равно +1, если
равно +1, если ![]() лежит вдоль границы; -1 – в
противоположном случае; 0 – если
лежит вдоль границы; -1 – в
противоположном случае; 0 – если ![]() ни одно из ребер
ни одно из ребер ![]() . Следовательно, матрица
. Следовательно, матрица ![]() имеет индексы
имеет индексы ![]() и
и ![]() .
.
Аналогично для ориентации тетраэдра.



![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() - векторы
- векторы ![]() -
образуют положительную систему отсчета («координат»).
-
образуют положительную систему отсчета («координат»).
Здесь
аналогично определяется матрица ![]() , если грань
, если грань ![]() есть граница тетраэдра, знак зависит от
ориентации
есть граница тетраэдра, знак зависит от
ориентации ![]() и от согласования её с границей тетраэдра
и от согласования её с границей тетраэдра ![]() .
.
Whitneyelements (WE)
Теперь определим функцию или векторное поле для всех сеточных симплексов. Для WE справедливо тождество
![]() в
в ![]() (1)
(1)
![]() - это оболочка всех
- это оболочка всех ![]() симплексов (пространство).
симплексов (пространство).
![]() (
(![]() ) – конечномерное
пространство. Это сеточные пространства,
) – конечномерное
пространство. Это сеточные пространства, ![]() и
и ![]() .
.
Степень 1
(![]() )
)
С ребром ![]() мы ассоциируем векторное поле
мы ассоциируем векторное поле
![]() (2)
(2)
и обозначим ![]() конечномерное пространство, порождаемое
конечномерное пространство, порождаемое ![]() симплексами.
симплексами.
Степень 2 (![]() )
) ![]()
С гранью ![]() мы ассоциируем векторное поле:
мы ассоциируем векторное поле:
![]() (3)
(3)
Степень 3 (![]() )
) ![]()
![]() порождается функциями
порождается функциями ![]() , каждая из которых для одного тетраэдра
, каждая из которых для одного тетраэдра ![]() равна
равна 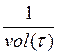 в
в ![]() и 0 вне его. Аналитическое выражение
аналогично (2) и (3).
и 0 вне его. Аналитическое выражение
аналогично (2) и (3).
 |


![]()
![]()
 |
![]()
![]()
I

![]()


![]()
![]()
![]()
![]()
![]()
II
I.
“edge - element”
или Whitney element степени 1, ассоциированный с ребром ![]() .
Это единичный тетраэдр, в котором - одно из ребер.
.
Это единичный тетраэдр, в котором - одно из ребер.
II.
“face - element”
или Whitney element степени 2, ассоциированный с гранью ![]() .
Это единичный тетраэдр, в котором - одна из граней.
.
Это единичный тетраэдр, в котором - одна из граней.
![]()
I.
В точке m: ![]() из (2) и этот вектор ортогонален к грани,
противоположной узлу m.
из (2) и этот вектор ортогонален к грани,
противоположной узлу m.
II.
В точке m: ![]() из (3) и этот вектор ортогонален и к
из (3) и этот вектор ортогонален и к ![]() и к
и к ![]() , и,
следовательно параллелен плоскости, противоположной граням
, и,
следовательно параллелен плоскости, противоположной граням ![]() и
и ![]() , то
есть является их пересечением, а именно ребром
, то
есть является их пересечением, а именно ребром ![]()
Таким
образом, любым симплексом ![]() связано поле, скалярно-
или векторозначное. Эти поля есть Whitney элементы. Их основные свойства:
связано поле, скалярно-
или векторозначное. Эти поля есть Whitney элементы. Их основные свойства:
·
значение ![]() в узле
в узле ![]() есть
1 (0 в других узлах);
есть
1 (0 в других узлах);
·
циркуляция ![]() вдоль ребра
вдоль ребра ![]() равна 1;
равна 1;
·
поток ![]() через грань
через грань ![]() равен 1;
равен 1;
·
интеграл от ![]() по тетраэдру
по тетраэдру ![]() равен 1 (и, конечно, в каждом случае, 0
для других симплексов).
равен 1 (и, конечно, в каждом случае, 0
для других симплексов).
В
барицентрических координатах ![]()
![]() для тетраэдра:
для тетраэдра:

 D(0,0,0,1)
D(0,0,0,1)
° ![]()
![]()
![]() A(1,0,0,0) °
A(1,0,0,0) °
![]()
![]() C(0,0,1,0)
C(0,0,1,0)
B(0,1,0,0)
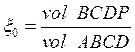
Edge-vector – элементные базисные функции:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
edge-элементные векторные базисные градиентные базисные функции функции
Face-vector basis functions
Восемь базисных функций, ассоциированных с гранью (с неизвестными на грани) определяются так:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Окончательно, ![]() ,
,
![]() .
.
Множество базисных функций является иерархическим, так что
конечноэлементное пространство ![]() , натянутое на базисные
функции степени не ниже 1 (т.е. 1 и более), полностью включено в пространство
, натянутое на базисные
функции степени не ниже 1 (т.е. 1 и более), полностью включено в пространство ![]() , которое натянуто на базисные функции
степени не ниже 2 (т.е. 2 и более).
, которое натянуто на базисные функции
степени не ниже 2 (т.е. 2 и более).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.