Языки и грамматики

Страницы работы

5 страниц (Word-файл)
Скачать файл

Фрагмент текста работы

1.  Принадлежит ли цепочка 01011010 языку L(G), если G=<{S, A, B}, A={0,1}, P, S>, где P={S®0S1½AS½BS1½e, A®S01½0A½1, B®1S0½B0½0}?
2.  Определить язык, порожденный грамматикой G=<N, A, P, S>:

a)  N={S, 0, 1}, A={a, b}, P={S®10a½1S, 0®b1, 1®a};

b)  N={S, 0, 1, 2}, A={3, 4}, P={S®S312½302, 0®21, 12®4, 2®e};

c)  N={S, A, B, C, D}, A={0, 1}, P={S®10A1½01B0½1CD1½D01, A®0A1½1B1½0C, B®1C½0A11½B0, C®A10½B1, D®10½A00½B0½1C};

d)  N={S, 0, 1, 2, 3}, A={a, b, c}, P={S®013½S013, a2a®abca, 3®ab, 1a®caa, 0ca®c};

e)  N={S, A, B, C, D}, A={0, 1}, P={S®0A0½1B0½1D1½0C1, A®01B½B1, C1®A10½0A0, 1B®0C½C11, D®A0½1C1½0D0½11½B00}.

3.  Определить состав терминального и нетерминального словарей грамматики G=<N, A, P, S> с правилами P={S®BC½AD½DE½SE½AB, A®EBD½AC½E, D®AB½DE½A, ED®CB½AE½BC, C®A½BC½E, B®A½BCD, CB®A½B, AEC®EC½AC½A}.
4.  Построить грамматику, порождающую язык:

a)  L={0n1k2n½n³1, k³0};

b)  L={0n1m2m3n½n³1, m³1};

c)  L={0n1n1m0m½n³1, m³1};

d)  L={an111bm½n³1, m³n};

e)  L={1n0am!!!bm02k½n³1, m³1, k³n};

f)  L={(an=bn)(cm=dm)½n³1, m³1};

g)  L={an–bm½n³1, m³1}U{ck+dk½k³1}.


5.  Пусть грамматика G=<N, A, P, S> имеют вид: N={S, A, B}, A={a, b} P={S®AB, A®Aa½bB, B®a½Sb}. Построить деревья выводов цепочек:

а) baabaab,b) bBABb,                    c) baSb.

6.  Построить левый и правый выводы цепочки baabaab в грамматике из задания 4.
7.  Построить левый вывод цепочки if bÙb then if bÚb then s else s else s в грамматике G=<{S, B}, {b, s, Ù, Ú, if, then, else}, { S®if B then S else S½s, B®BÙB½BÚB½b}, S>.
8.  Можно ли в грамматике G=<{S}, {1}, {S®S1S}, S> вывести цепочку 131 и, если нет, то каким образом следует изменить правила грамматики G, чтобы это стало возможно?
9.  Найти отличие языков L(G1) и L(G2), если Gi=<Ni, Ai, Pi, S>, i=1,2, N1=N2={S, A, B}, A1=A2={0,1,2}, P1={S®0A1, A®B½0A1, B®2B½e} P2={S®0A1, A®B½0A1, B®2B½2}.
10.  Чем отличаются грамматики G1 и G2 языков             L(G1)={an0mbn½n³1, m³0} и L(G2)={an0kbn½n³1, k³1}?
11.  Определить грамматику, порождающую язык:

a)  L(G)=L1\(L2UL3), L1={w½wÎ{0,1}*}, L2={0w1½wÎ{0,1}*}, L3={0w0½wÎ{0,1}*}.

b)  L(G)=L2\L1, L1={b2w½wÎ{a,b}*}, L2={w–1½wÎ{a,b}*}.

c)  L(G)=L1UL2, L1={0n1n½n³2}, L2={w½wÎ{0,1}*}.

d)  L(G)=L2\L1, L1={w½wÎ{0,1}*}, L2={0n1n½n³1}

e)  L(G)=L1IL2, L1={01n1n0½n³1}, L2={01m0½m³0}.

f)  L(G)=L1\L2, L1={ab2ka½k³0}, L2={abma½m³1}.

12.  Является ли грамматика G=<N, A, P, S>, с правилами P={S®A0, A®B0, B®A1} грамматикой языка L1\L2, где L1={012k0½k³1}, L2={01m0½m³0}.
13.  Чему равно кардинальное число множества терминальных цепочек, порожденных грамматикой G=<N, A, P, S>, если:

a)  N={S, A}, A={a, b}, P={S®aAb, A®aAb½e};

b)  L(G)={anbncmdm½n³1, m³1},

c)  L(G)=L1UL2, L1={anbn½n³1}, L2={0m1m2m½m³1}.


14.  Среди всех раннее рассмотренных языков найти пары эквивалентных.
15.  На декартовом произведении L1´L2, где L1={anbn½n³1}, L2={a2kb2k½k³1} определено бинарное отношение R={(x, y)½ xÎL1, yÎL2, длина цепочки x равна длине цепочки y}. Исследовать Rна симметричность, рефлексивность и транзитивность.
16.  Задано бинарное отношение R={(x, y)½ xÎL1, yÎL2, x – подцепочка цепочки y} на множестве L1´L2, где L1={0n1k1n½n³1, k³0}, L2={0n1n½n³1}. Является ли оно отношением эквивалентности?
17.  Найти результат подстановки языка L(G1) в язык L(G2), если Gi=(Ni, Ai, Pi, Si), i=1,2 и

a)  N1={S1}, A1={0}, P1={S1®S10½e},       N2={S2}, A2={1}, P2={S2®13S20½e};

b)    N1={S1, S3}, A1={0, 1}, P1={S1®0S211, S2®0S21½e},

N2={S2, S4}, A2={a, b}, P2={S2®a2S4b, S4®bS4a½e};

18.  Построить грамматику для языка – результата подстановки языка L2 в язык L1, если L1={01n½n³1} и L2={anbn½n³1}.
19.  С помощью подходящих операций постройте язык L={(01)n½n³0} из языков:

L1={an½n³0},        L2={bn½n³0},     L3={01},      L4={e},     L5={w½wÎ{a,b}*},                                       L6={w½wÎ{b,c}*}.

20.  Из языков задания 19 постройте язык L={01an½n³1}.
21.  Из языков задания 19 постройте язык L={w½wÎ{a,b,c}*}.
22.  Пусть грамматика G1=<N1, A1, P1, S1> определяет язык L1, а грамматика G2=<N2, A2, P2, S2> определяет язык L2, постройте грамматику G=<N, A, P, S> для языков:

a)  L=L1UL2                                           b) L=L1°L2.

23.  Пусть А-грамматика G1=<N1, A1, P1, S1> определяет А-язык L1, а А-грамматика G2=<N2, A2, P2, S2> определяет А-язык L2, постройте А-грамматику G=<N, A, P, S> для языков:

a)  L=L1UL2                                           b) L=L1°L2.

24.  Какие из приведенных ниже грамматик являются А-грамматиками?

a)  G1=<{a,b}, {S}, {S®ab½aSb}, S>,

b)  G2=<{a,b}, {S,A,B}, {S®AB, A®aA½e, B®bB½e }, S>,

c)  G3=<{a,b}, {S}, {S®aS½bS½e}, S>,

d)  G4=<{a,b}, {S,A}, {S®aSb½aA½e, A®aA½e}, S>,

e)  G5=<{a,b}, {S,A,B}, {S®aA½bB, A®aA½bA, B®aB½bB½b}, S>,

f)  G6=<{a,b}, {S}, {S®aS½Sb½a½b}, S>,

g)  G7=<{3,4}, {S,1,2}, {S®S312½302, 0®21, 12®4, 2®e}, S>,

h)  G8=<{a,b,1,2}, {S,A,B}, {S®aB½bB½a½b, B®AB, A®a½b½1½2}, S>,

i)  G9=<{a,b}, {S,A,B}, {S®aАа, A®aABa½b, aB®Ba, bB®bb}, S>.

25.  Какие из грамматик из задания 24 являются линейными?
26.  Какие из грамматик из задания 24 являются КС-грамматиками?
27.  Какие из грамматик из задания 24 являются НС-грамматиками?
28.  Какие из грамматик из задания 24 задают А-языки?
29.  Какие из грамматик из задания 24 задают КС-языки?
30.  Какие из грамматик из задания 24 задают НС-языки?
31.  Докажите, что если грамматика G=<N, A, P, S> содержит правила P' (т.е. P'ÌP), то она неоднозначна.

a)  P'={A®AA½a};

b)  P'={A®AaA};

c)  P'={A®aA½Ab};

d)  P'={A®aA½aAb};

e)  P'={A®Ab½aAb}.


32.  Определите какие из следующих языков являются неоднозначными:

L1={anbmcmdn½n,m³1}U{ambmcndn½ n,m³1},

L2={anbmckdmpn½n,m,k³1}I{ambmckdnpn ½n,m,k³1},

L3={anbm½n,m³1, m³n}.

33.  Определите какие из следующих языков

L1={(a,ba)*},

L2={(ab)m½m³0},

L3=L1UL2,

L4=L1°L2

L5={anbmdk½n,m,k³1},

L6={anbmdk½n,m,k³1, m³n},

L7={(ab)n(ab)n½n³0},

L8={w½wÎ{a,b}*}

L9=L7UL8,

L10=L7°L8,

L11={anbncmdm½n,m,k³1, m³n},

L12={ambncndm½n,m,k³0, m³n},

L13=L5UL7,

L14=L5°L7


являются              a) А-языками          b) КС-языками              c) НС-языками?

34.  Постройте А-грамматику для языков

L1={(01)n(10)m½n³0, m³1}, L2={anba½n³0}.


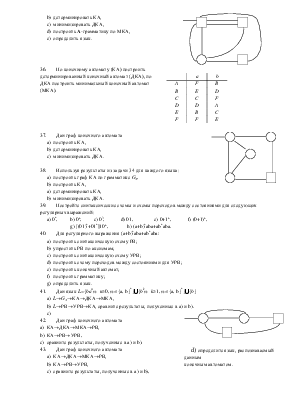
35.  Дан граф конечного автомата

a)  построить КА,

b)  детерминировать КА,

c)  минимизировать ДКА,

d)  построить А-грамматику по МКА,

e)  определить язык.


36.  По конечному автомату (КА) построить детерминированный конечный автомат (ДКА), по ДКА построить минимальный конечный автомат (МКА).

a

b

A

F

B

B

E

D

C

C

F

D

D

A

E

B

C

F

F

E

37.  Дан граф конечного автомата

a)  построить КА,

b)  детерминировать КА,

c)  минимизировать ДКА.

38.  Используя результаты из задачи 34 для каждого языка:

a)  построить граф КА по грамматике GA,

b)  построить КА,



a)  детерминировать КА,

b)  минимизировать ДКА.

39.  Постройте синтаксические схемы и схемы переходов между состояниями для следующих регулярных выражений:

a) 0*,         b) 0+,        c) 03,           d) 01,               e) 0+1+,            f) (0+1)+,                  

g) [(01)*+01*]10+,              h) (a+b)*aba+ab*aba.

40.  Для регулярного выражения (a+b)*aba+ab*aba:

a)  построить синтаксическую схему РВ;

b)  упростить РВ по аксиомам;

c)  построить синтаксическую схему УРВ;

d)  построить схему переходов между состояниями для УРВ;

e)  построить конечный автомат;

f)  построить грамматику;

g)  определить язык.

41.  Дан язык L={banw½n³0, wÎ{a, b}*}U{bkw½k³1, wÎ{a, b}*}U{b}

a)  L®GA®КА®ДКА®МКА,

b)  L®РВ®УРВ®КА, сравните результаты, полученные в a) и b).


c)   

42.  Дан граф конечного автомата

a)  КА®ДКА®МКА®РВ,

b)  КА®РВ®УРВ,

c)  сравните результаты, полученные в a) и b).


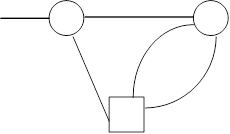
43.  Дан граф конечного автомата

a)  КА®ДКА®МКА®РВ,

b)  КА®РВ®УРВ,

c)  сравните результаты, полученные в a) и b),

d)  определите язык, распознаваемый данным конечным автоматом.


44.  В грамматике G=<{a, b}, {S, A, B, C}, {S®AB, A®a, B®b, C®CA}, S> найдите и устраните непродуктивные символы.
45.  В грамматике G=<{a, b, c, d, e, f, g}, {S, A, B, Q}, P, S> найдите и устраните недостижимые символы, если:

a)  P={S®aAcg3aBd, A®aAc½d, B®aBd½c, Q®aBc½daf},

b)  P={S®aAb½cBd, A®aA½Ab½gg, B®cBd½ff, Q®cAb½gf}.

46.  В грамматике G=<N, T, P, S> найдите и устраните бесполезные символы, если:

a)  N={S, A, B}, T={a, b}, P={S®A½a, A®AB, B®b},

b)  N={S, A, B, D, F, C}, T={p, d, g, f}, P={S®AB½Ap, A®g, B®DF½d, D®d, F®fF, C®p},

c)  N={S, A, B}, T={a, b}, P={S®AB½Ap, A®aB½bS½b, B®AB½Ba, B®aS½b}.

47.  Используя в качестве примера грамматики из предыдущего задания докажите, что шаги в алгоритме удаления бесполезных символов не перестановочны (т.е. нельзя вначале удалить недостижимые символы, а потом удалить непродуктивные).
48.  Преобразуйте грамматику G=<N, T, P, S> в грамматику без e-правил, если:

Информация о работе

ВУЗ:
Новосибирский государственный технический университет (НГТУ)
Размер файла:
126 Kb
Скачали:
0
Скачать файл