Экзаменационные задачи по сетям, процессам и множествам

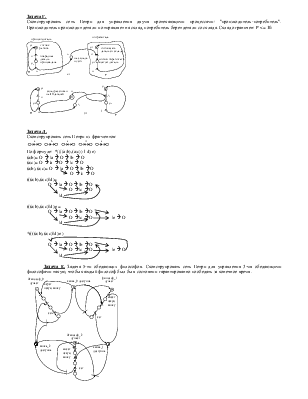
Пусть есть три обрабатывающих устройства t₀, t₁, t_2, организованные в виде конвейера. Это могут быть, например, станки на заводе или функциональные устройства конвейерного процессора и вообще любой конвейер, в котором каждое обрабатывающее устройство выполняет лишь часть общей работы, а результат будет выработан лишь последним из них.

Особенностью нашего конвейера является ограниченность емкости мест p₁ и  p₂. Место p₁  может вместить лишь два результата (место p₁  сети должно быть 2-ограниченым) предшествующего этапа работы конвейера (вырабатывается переходом  t₀ ), а место p₂ - три. Символ n в месте p₀ означает наличие n фишек в нем, n - целое положительной число.

Сеть Петри, обеспечивающая необходимое прямое управление, приведена на рис. 3.7. Понятно, что в месте p₁ не может накопиться более 2-х фишек при любых порядках срабатывания переходов сети. Две фишки в месте p₄ говорят о наличии в  p₁ свободных емкостей для размещения 2-х  результатов срабатывания перехода  t₀ . Места p₁  и  p₂ часто еще называют асинхронными каналами, с их помощью реализуется программирование средствами асинхронного message passing interface (см. параграф 4.3.).

Задача Г.

Сконструировать сеть Петри для управления двумя протекающими процессами: "производитель-потребитель". Производитель производит детали и отправляет на склад, потребитель берет детали со склада. Склад ограничен: Р <= 10.

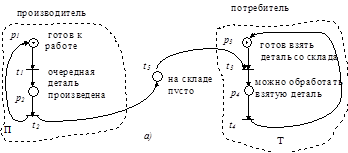
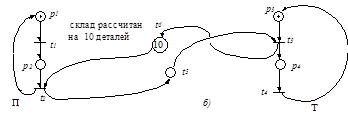
Задача Д.

Сконструировать сеть Петри из фрагментов:

По формуле:  *((((a;b),(a;c)) || d);e)

(a;b)= O à |a à O à |b à O

(a;c)= O à |a à O à |c à O

(a;b),(a;c)= O à |a à O à |b à O

                                      O à |c à O

(((a;b),(a;c)||d)=

    O à |a à O à |b à O

                                     O à |c à O

|d

(((a;b),(a;c)||d);e=

    O à |a à O à |b à O

                                     O à |c à O                 |e à O

|d

*((((a;b),(a;c)||d);e)

 

    O à |a à O à |b à O

                                     O à |c à O                 |e à O

|d

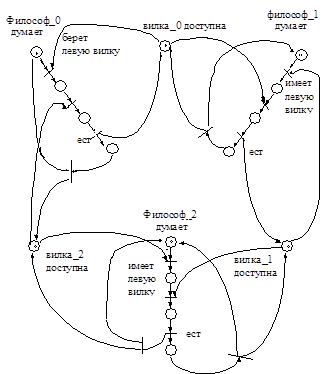
Задача Е. Задача 5-ти обедающих философов. Сконструировать сеть Петри для управления 3-мя обедающими философами такую, чтобы каждый философ был бы в состоянии гарантированно пообедать за конечное время.

Задача Ж.

Ж) Программа разделения двух множеств (Э.Дейкстра). Даны два множества натуральных чисел S и T. Сохраняя мощности множеств, необходимо собрать в S наименьшие элементы множества SÈT , а в T - наибольшие.

Small::                                                             |    Large::

mx:=max(S);  a!mx;  S:=S-{mx};              |       a?y;  T:=TÈ{y};  mn:=min(T);

b?x;  S:=SÈ{x};  mx:=max(S);                  |       b!mn;  T:=T-{mn};  mn:=min(T);

*[mx > x ->                                                 |       *[mn < y ->

a!mx;  S := S-{mx};  b?x                      |            a?y;  T:=TÈ{y};  mn:=min(T);  b!mn;

S:=SÈ{x};  mx:=max(S);                      |             T:=T-{mn};  mn:=min(T);

]  stop                                                        |          ]  stop

Написать неравенства при которых эта программа работает некорректно. Проверить программу на наборах множеств:  S={5,10,15,20}и T={17,18,30,40}; S={5,10,15,20}и T={14,17,18,30,40}.

Решение.

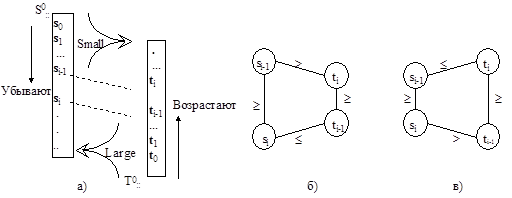Рис. 3.15.

Полученные выше условия некорректного поведения программы определены для (i-1)-го и i-го максимальных значений множества S и для (i-1)-го и i-го минимальных значений множества Т, (i =1,2, ...). Эти условия представлены диаграммами  на рис. 3.15.б) и 3.15.в).

Иными словами, если между упорядоченными по убыванию элементами множества S и упорядоченными по возрастанию элементами множества Т на одном и том же расстоянии от начала выполнится одно из отношений рис. 3.15,б) или рис. 3.15,в), то исследуемая программа будет работать некорректно: она входит в дедлок.

Можно указать тестовый пример, на котором эта программа работает некорректно: S={5,10,15,20}, T={17,18,30,40,60}. Этот пример относится к первому типу некорректностей при i=1: первое же вхождение процесса Large в цикл приводит к дедлоку, поскольку Small завершится, не входя в цикл.

Задача З.

Задача "читатели-писатели". Писатели только модифицируют разделяемый объект, читатели - только считывают значение. Написать фрагменты программ работы этих процессов с помощью семафоров.

Begin

               Semaphore mem_work:=1; reader_work:=1;

Int nOfReaders:=0;

Parbegin

Reader: begin

½A1:P(reader_work);

½If (nOfReaders=0) then p(mem_work);

½NOfReaders:=NOfReaders+1;

½V(reader_work);

½Reading;

½P(reader_work);

½If (nOfReaders=0) then v(mem_work);

½V(reader_work);

½Data processing

½Goto A1;

end

writter: begin

½A2: data producing

½P(mem_work);

½Data writting

½V(mem_work);

½Goto A2;

End

Parend

end

Задача И.

Задача взаимного исключения. Имеется несколько циклических процессов. Каждый процесс на каждом своем цикле имеет доступ к некоторому общему для всех процессов ресурсу и конфликтует с другими процессами при доступе к нему. Написать фрагмент программы для i -го процесса этой задачи.

Begin

Semaphore free:=1;

Parbegin

Pi:Li: begin

½P(free);

½{ do something critical };

½V(free);

½{ do some };

½goto Li;

½end;

parend;

end.

Задача К.

Задача "производитель-потребитель". Производитель производит продукцию и отсылает в ограниченный буфер, потребитель берет из этого буфера продукцию. Оба процесса циклические и конфликтуют при доступе к общему буферу. Написать фрагменты программ работы этих процессов с помощью семафоров