Экзаменационные билеты по теории вероятности

Билеты целиком

Билет №16

1.  Свойства вероятности.

2.  Экспоненциальное распределение: определение, обозначение, характеристическая функция распределения, ее использование для вычисления числовых характеристик.

3.  Момент случайных величин,  -квантиль, мода, медиана.

4.  Теорема Линдеберга.

5.  Случайная точка  имеет равномерное распределение на , , , .Исследовать события ,  и  на непрерывность (парную и в совокупности).

6.  Из 10 студентов, 3 – подготовлены отлично, 4 – хорошо, 2 – посредственно, 1- плохо, т.е. выучили 20, 16, 10 и 5 билетов соответственно. Всего 20 билетов. Найти вероятность того, что вызванный наугад студент ответит на три вопроса. Какова вероятность того, что это оказался плохо подготовленный студент.

7.  Случайная величина  имеет нормальное распределение с параметрами 0 и1, случайная величина . Найти закон распределения случайной величины, ее математическое ожидание и дисперсию. Найти вероятность попадания случайной величины  в интервал .

8.  Случайные величины  и  независимы и одинаково распределены. Найти  в случае, если  и  имеют распределение .

9.  . При какой  вероятность попадания случайной величины в заданный интервал  будет наибольшей?

Билет №4

1.  Аксиоматическое определение вероятности. Аксиомы непрерывности.

2.  Равномерное распределение: определение, обозначение, характеристическая функция, ее использование для вычисления числовых характеристик.

3.  Условие распределения для двух непрерывных случайных величин. Условие функции распределения и плотности распределения.

4.  Теорема Линдеберга.

5.  Вероятность того, что деталь не стандартная . Найти сколько деталей надо отобрать, чтобы с вероятностью, равной , можно было утверждать, что относительная частота появления нестандартных деталей среди отобранных отклониться от постоянной вероятности  по абсолютной величине не более, чем на .

6.  В первой урне 6 черных и 4 белых шара, во второй 5 белых и 4 черных шара. Из первой урны перекладывают во вторую один шар, после чего из второй извлекают один шар. Найти вероятность, что этот шар – белый. Какова вероятность, что при этом из первой урны во вторую был переложен черный шар.

7.  Известно, что при бросании двух игральных костей сумма выпавших очков нечетна.  - сумма выпавших очков. Найти закон распределения, математическое ожидание, дисперсию случайной величины . Построить график функции распределения и ряда распределения. Найти вероятность .

8.  Случайные величины  и  независимы и нормально распределены с параметрами 0 и 1, и 0 и 2 соответственно. Вычислить вероятность попадания случайной величины  в эллипс с полуосями 1 и 2 и центром в начале координат.

9.  Случайные величины  и  независимы и одинаково распределены по закону Пуассона с параметром 1. Найти плотность распределения случайной величины .

Билет №11

1.  Задача о совпадениях.

2.  Закон больших чисел для одинаково распределенных случайных величин. Теорема Бернулли.

3.  Условные распределения для двух случайных величин.

4.  Последовательность независимых событий. Теорема Бореля-Кантелли.

5.   и  случайным образом выбраны из отрезка  и  соответственно. Найти вероятность того, что их произведение не превосходит .

6.  Из урны, содержащей 3 белых и 2 черных шара, переложено 2 шара в урну, где уже есть 4 белых и 4 черных шара. Какова вероятность вытянуть белый шар из второй урны? Какова вероятность, что при этом во вторую урну из первой переложили 2 черных шара?

7.  . Найти закон распределения случайных величин  и .

8.  Найти , если  имеет равномерное распределение на ,  - показательное распределение с параметром .

9.  Случайная величина  задана совместной плотностью распределения 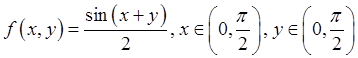. Найти математическое ожидание, дисперсию, ковариацию и коэффициент корреляции, а также ковариационную матрицу случайных величин  и .

Билет №12

1.  Интегральная формула Муавра-Лапласа.

2.  Равномерное распределение: определение, обозначение, характеристическая функция, ее использование для вычисления числовых характеристик.

3.  Математическое ожидание случайных величин, его свойства.

4.  Неравенство Колмогорова.

5.  Числа  и  случайным образом выбраны на отрезке . Найти вероятность того, что корни  не существуют в множестве действительных чисел.

6.  Первое из 4 орудий батареи пристрелено так, что вероятность попадания составляет 0.4. Остальные орудия попадают с вероятностью 0.2. Для поражения цели достаточно одного попадания. Найти вероятность поражения цели одним орудием.

7.  Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 1 мм и средним квадратичным отклонением 2 мм. Найти:

-  вероятность того, что отклонение от номинала отрицательное.

-  процент деталей, для которых изменится отклонение от номинала в пределах  мм.

-  верхнюю границу отклонения от номинала, обеспеченную с вероятностью