






Министерство образования Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра прикладной математики
Численные методы
Группа: ПМ-12
Студент: Дуркин Д.С.
Кичаева Н.А.
2003
В данной работе мы написали программу решения СЛАУ ![]() с помощью прямого метода, основанного на
разложении матрицы А на произведение
с помощью прямого метода, основанного на
разложении матрицы А на произведение ![]() , где L - нижнетреугольная матрица, а U - верхнетреугольная матрица с единицами на главной
диагонали. В силу того, что исходная матрица задается в профильном формате,
алгоритм
, где L - нижнетреугольная матрица, а U - верхнетреугольная матрица с единицами на главной
диагонали. В силу того, что исходная матрица задается в профильном формате,
алгоритм ![]() разложения разработан для профильного
формата.
разложения разработан для профильного
формата.
Согласно теореме о ![]() разложении
этот метод применим только для матрицы А, все угловые миноры которой не равны
нулю. В противном случае разложение не возможно.
разложении
этот метод применим только для матрицы А, все угловые миноры которой не равны
нулю. В противном случае разложение не возможно.
Алгоритм получения ![]() разложения
имеет следующий вид:
разложения
имеет следующий вид:
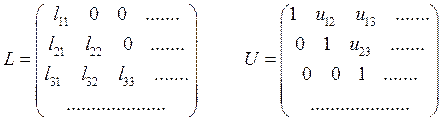
Отсюда
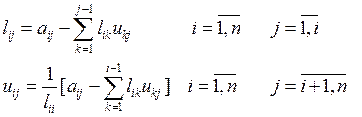
Далее решим систему ![]() с
нижнетреугольной матрицей
с
нижнетреугольной матрицей ![]() . Алгоритм получения
формул для прямого хода имеет вид:
. Алгоритм получения
формул для прямого хода имеет вид:
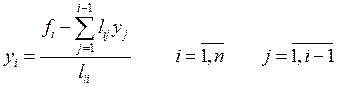
Для обратного хода ![]() , где U - верхнетреугольная матрица с
единицами на главной диагонали формулы получения вектора x
имеют вид:
, где U - верхнетреугольная матрица с
единицами на главной диагонали формулы получения вектора x
имеют вид:
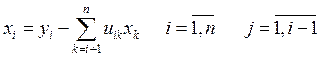
В лабораторной работе также реализован метод Гаусса с выбором ведущего элемента для плотных матриц.
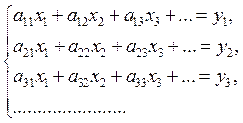
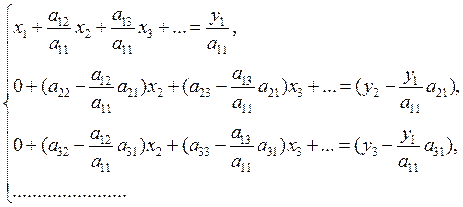
Подсчитаем количество действий, затрачиваемых для решения СЛАУ методом Гаусса.
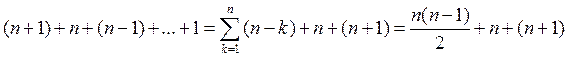
![]() Посчитаем
сначала количество умножений для вычисления
Посчитаем
сначала количество умножений для вычисления ![]() .
.
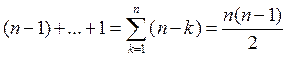
Теперь посчитаем количество действий для
вычисления коэффициентов ![]() .
.
![]()
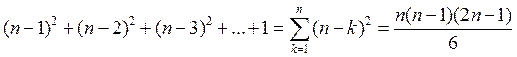
В итоге получаем:
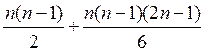
Замечание:
Для тех коэффициентов, про которые заранее известно, что они обнуляются, действия не учитывались!
Количество суммирований равно количеству умножений.
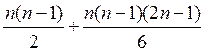
Таким образом, при больших ![]() число действий
равно приблизительно
число действий
равно приблизительно ![]() .
.
Теперь, исходя из описанных выше формул, посчитаем
количество действий, затрачиваемых для решения СЛАУ ![]() методом
методом
![]() - разложения:
- разложения:
·
![]() -разложение:
-разложение:
1. Суммирование
Посчитаем сначала для
диагональных элементов нижнетреугольной матницы, т.е. для ![]() .
.
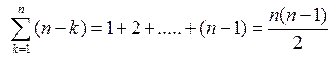
Для вычисления элементов нижнего треугольника![]() (без диагональных ) требуется
(без диагональных ) требуется 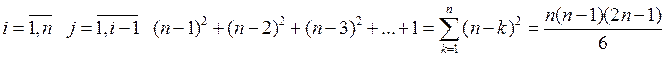 операций.
операций.
Для вычисления элементов верхнего
треугольника ![]() необходимо следующее количество действий.
необходимо следующее количество действий.
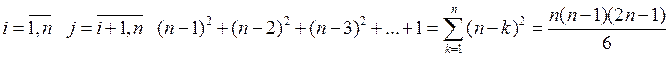
В итоге получаем 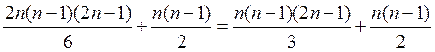 суммирований.
суммирований.
2. Умножение
Поскольку при данном алгоритме ![]() разложения количество суммирований
совпадает с количеством умножений, то мы имеем
разложения количество суммирований
совпадает с количеством умножений, то мы имеем 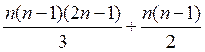 умножений.
умножений.
3.Деление
В данном случае деление требуется
только для вычисления элементов верхнетреугольной матрицы ![]() , причем для каждого
, причем для каждого ![]() требуется ровно одно деление на
диагональный элемент, то количество делений совпадает с количеством ненулевых
элементов матрицы
требуется ровно одно деление на
диагональный элемент, то количество делений совпадает с количеством ненулевых
элементов матрицы ![]() ( исключая диагональные элементы
).
( исключая диагональные элементы
).
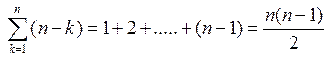
· Вычисление
вектора y( ![]() ):
):
1. Суммирование
Для каждого i ![]() требует
(i-1) суммирований, т.е.
требует
(i-1) суммирований, т.е.
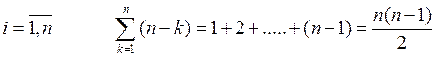
2. Умножение
Количество умножений здесь также совпадает
с количеством суммирований, поэтому мы имеем 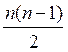 умножений.
умножений.
3.Деление
При вычислении все элементы ![]() делятся на диагональные элементы матрицы
делятся на диагональные элементы матрицы ![]() по одному разу, отсюда количество делений
совпадает с количеством элементов
по одному разу, отсюда количество делений
совпадает с количеством элементов ![]() , т.е.
, т.е. ![]() .
.
· Вычисление
вектора x(![]()
):
1. Суммирование
Для каждого i ![]() требует
тоже (i-1) суммирований, т.е.
требует
тоже (i-1) суммирований, т.е.
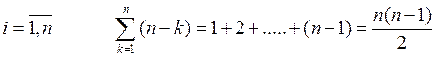
2. Умножение
Количество умножений- 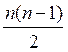 .
.
В итоге мы имеем, что
количество операций умножений, равно как и операций сложения, в методе ![]() -разложения при достаточно больших
будет
-разложения при достаточно больших
будет ![]() . Таким образом, подобных операций в методе
Гаусса, как видно из вычислений, приведенных выше, будет в 2 раза меньше!
. Таким образом, подобных операций в методе
Гаусса, как видно из вычислений, приведенных выше, будет в 2 раза меньше!
Тестирование
1.Матрица с нулевым угловым минором
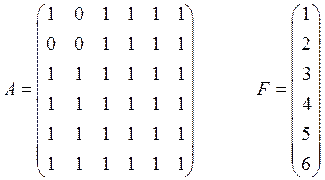
результат работы программы:There is no LU decomposition!
2. Матрица с нулевой диагональю
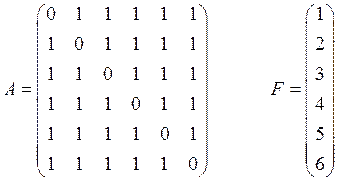
результат работы программы:There is no LU decomposition!
3. Профильная матрица с дробными элементами
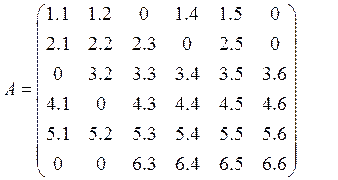
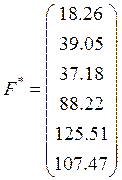
результата выполнения программы:
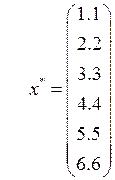



Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.