




Министерство образования
Российской Федерации
Новосибирский государственный
технический университет
кафедра прикладной математики
Расчетно-графическая работа теме
«ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ КОШИ»
Студент: Дмитрий Койфман
Вариант: 8
Преподаватель: Иткина Н.Б.
Вариант задания:
Для прогноза ![]() подобрать оптимальную коррекцию.
Обосновать выбор.
подобрать оптимальную коррекцию.
Обосновать выбор.
Пусть дана задача Коши:
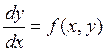 ;
; ![]() .
.
И для такой задачи рассмотрим прогноз вида:
![]()
При подстановке в данный прогноз полинома 3-ей степени имеем:
![]()
Приравняв коэффициенты в правой и левой частях при соответствующих степенях h, получим систему для определения коэффициентов:
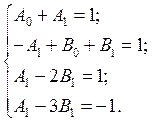
Выберем в качестве параметра коэффициент, встречающийся во всех уравнениях, А1 и выразим через него остальные коэффициенты, используя первые три уравнения:
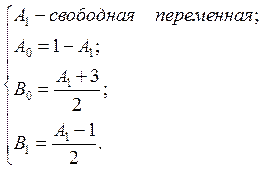
Полученное семейство прогнозов, которое даже без выбора A1 имеет порядок аппроксимации O(h2), исследуем на устойчивость.
Пусть ![]() , где un
– точное решение задачи в узле сетки, а yn
– численное решение.
, где un
– точное решение задачи в узле сетки, а yn
– численное решение.
![]() , где en – погрешность вычисления.
, где en – погрешность вычисления.
![]() .
.
Положим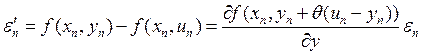 , где
, где ![]() (по
теореме о среднем значении функции, поскольку по условию f(x,y) непрерывна по y). Обозначим
(по
теореме о среднем значении функции, поскольку по условию f(x,y) непрерывна по y). Обозначим 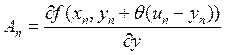 .
.
![]()
An можно считать ограниченной,
поэтому при исследовании асимптотической устойчивости (![]() )
)![]() :
:
![]() .
.
Его решение будем
искать в виде ![]() . Получим
. Получим
![]()
поделим на ![]() :
:
![]() .
.
Для нашего семейства получим уравнение:
![]() .
.
Корни данного уравнения:
![]()
Т.к. ![]() , сразу можем сделать вывод, что прогноз
будет условно устойчивым.
, сразу можем сделать вывод, что прогноз
будет условно устойчивым.
Также для
устойчивости необходимо выполнение условия ![]() .
.
Попробуем повысить порядок аппроксимации метода до O(h3) выбором A1. Рассмотрим четвертое уравнение в полученной системе с коэффициентами. Оно станет тождеством при A1=5, B1=2. Заметим, что подобный прогноз выходит за границы области устойчивости. Т.о. выбором параметра мы не можем добиться повышения порядка аппроксимации, хотя чем, больше мы выберем A1, тем меньше будет погрешность:
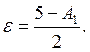
Возьмем в качестве основного (оптимального) прогноза следующий:
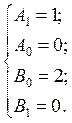
Теперь выберем коррекцию. Общий вид двухточечной коррекции имеет вид:
![]() .
.
Аналогичным образом построим семейство коррекций и исследуем его на устойчивость.
Для функции ![]() получим уравнение:
получим уравнение:
![]()
Система для нахождения коэффициентов:
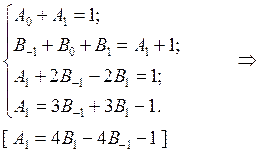
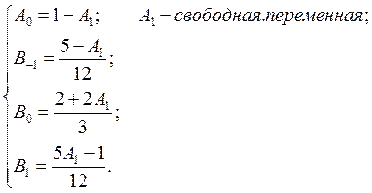
Запишем уравнение для погрешности:
![]()
если 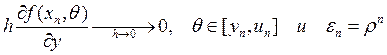 ,то:
,то:
![]() .
.
Или с учетом коэффициентов семейства:
![]() .
.
Корни данного
уравнения: ![]()
Т.к. ![]() , сразу можем сделать вывод, что коррекция
будет условно устойчивой.
, сразу можем сделать вывод, что коррекция
будет условно устойчивой.
Также для
устойчивости коррекции, так же, как и для прогноза, необходимо выполнение
условия ![]() .
.
Аналогично, прогнозу нельзя повысить и порядок аппроксимации коррекции:
![]()
Т.о.
оптимальной коррекцией предположительно является условно асимптотически
устойчивая: 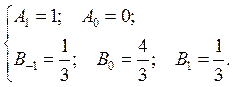
Экспериментально сравним использование различных коррекций:
1) оптимальный
прогноз с оптимальной коррекцией (![]() );
);
2) оптимальный
прогноз с неоптимальной, но устойчивой коррекцией из полученного семейства (![]() );
);
3) оптимальный
прогноз с коррекцией с меньшим порядком аппроксимации (т.е. не из полученного
семейства: берем только
первых три уравнения системы для коррекции: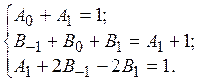 и
выбираем коэффициенты, например:
и
выбираем коэффициенты, например: 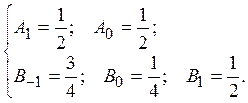 )
)
Также проверим правильность нахождения области устойчивости и полученные порядки аппроксимации.
Выводы:
Эксперименты подтвердили выбор оптимальной пары прогноз-коррекция для заданного вида прогноза. Во всех тестах эта пара превзошла другие протестированные.
Во всех экспериментах заметно, что величина ![]() ведет
себя также, как и точное значение (возрастает/убывает), причем изменяется
быстрее искомой функции, т.к проверялись устойчивые прогнозы-коррекции.
ведет
себя также, как и точное значение (возрастает/убывает), причем изменяется
быстрее искомой функции, т.к проверялись устойчивые прогнозы-коррекции.
Практически полученные порядки аппроксимации совпадают с теоретическими характеристиками методов.
Задание неустойчивой коррекции не позволяет использовать метод для
расчетов. Но применение неустойчивого прогноза возможно, благодаря влиянию
коррекции. Поэтому на практике можно считать оптимальным не прогноз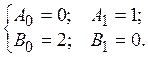 , а теоретически неустойчивый прогноз
, а теоретически неустойчивый прогноз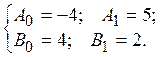
Результаты и сопутствующие выводы также прилагаются к таблицам.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.