Факторный анализ и исследования

полученных результатов видно, что в данном случае корреляционные матрицы существенно не изменились, и структура факторной матрицы осталась такой же.

Рассмотрим пример, когда исходные данные принадлежат к различным  шкалам, то есть  присутствуют последовательности дихотомических, количественных и ранговых  переменных. При нахождении корреляционной матрицы  последовательности ранговых и количественных переменных будем применять коэффициент Пирсона (табл.2.7). А во втором случае к последовательности ранговых переменных будем применять коэффициент Тау Кендала (табл.2.9).    Исходные данные возьмем из таблицы П.4 приложения.

Покажем, как в этих случаях будет выглядеть корреляционная матрица и матрица факторного отображения соответственно  (табл.2.8) и (табл.2.10).

Обобщенная дисперсия в первом случае составляет 89%, во втором -  95%.

Таблица 2.7.Корреляционная матрица

Таблица 2.8.Факторная матрица

Таблица 2.9.Корреляционная матрица

Таблица 2.10.Факторная матрица

Из полученных результатов видно, что корреляционная матрица меняет свою структуру, а соответственно меняется и матрица факторного отображения.

3. Программное обеспечение

3.1. Общие сведения

Программное обеспечение носит название: «Факторный анализ». Оно написано на языке С++ в среде разработки Borland C++ Builder 6, и предназначено для проведения факторного анализа разнотипных признаков.

3.2. Функциональные возможности

1.  Вычисление корреляционной матрицы;

2.  Выбор шкалы в к которой принадлежит исследуемый признак:

3.  Возможность ранжирования признаков;

4.  Вычислении матрицы факторного отображения;

5.  Имеется возможность выбора числа значащих факторов;

6.  Вычисление матрицы значений факторов.

3.3.  Порядок работы

Порядок работы:

1)  Прежде чем приступить к анализу необходимо загрузить исходные данные,делается это так: в меню файл-> “считать исходные данные”, о представлении исходных данных в файле можно прочитать в пункте Исходные данные.

2)    После того как данные считаны имеется возможность выбора типа шкалы, в которой мы хотим оценить данный  признак, имеется 3 варианта выбора (Рис.2.1): а) Дих выбирается, когда  исходные данные представлены в дихотомической шкале.

б) Ранг выбирается, когда  исходные данные представлены в шкале порядка или когда исходные данные рангами не являются, то при выборе данного пункта, данные автоматически преобразуются в ранги.

в) Колич выбирается, когда  исходные данные представлены в шкале отношений, при загрузки исходных данных выбирается по умолчанию.

3) Следующим этапом необходимым для исключения влияния не значимых факторов является выбор числа значимых признаков.

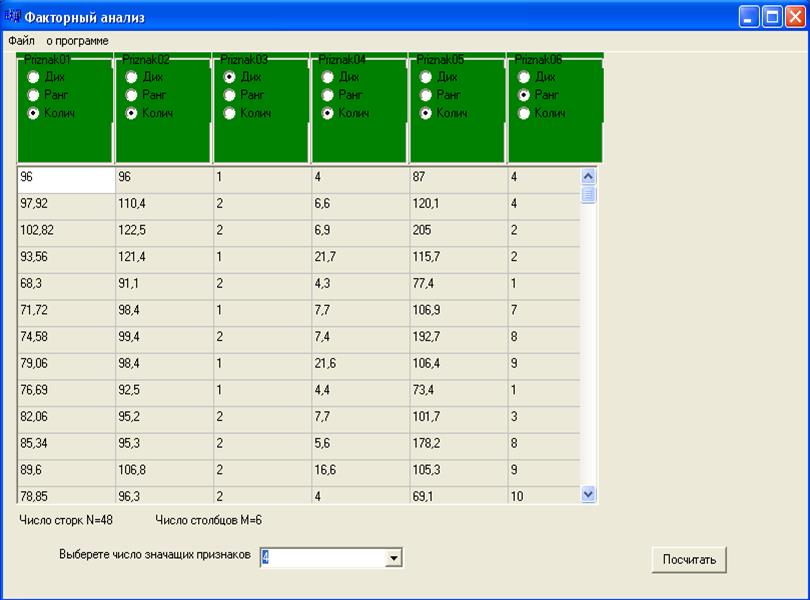
Рис2.1. Внешний вид программы после загрузки исходных данных.

4)  Для проведения факторного анализа необходимо не обходимо  нажать на кнопку «Посчитать», после чего появляется новая формав которой будут отображены «Корреляционная матрица» , «Матрица факторного отображения» и обобщенная дисперсия (Рис.2.2)

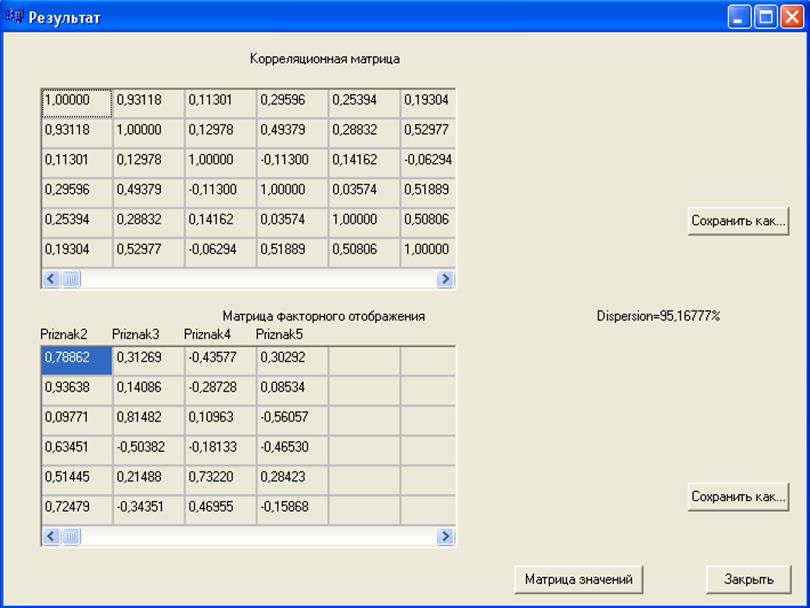
Рис.2.2. Результаты

5)  Признаки  Матрицы факторного отображения расположены в порядке убывания их вклада в обобщенную дисперсию.

6)  После нажатия на кнопку «Матрица значений» появится новая форма с изображением  матрицы факторных значений (Рис.2.3). 

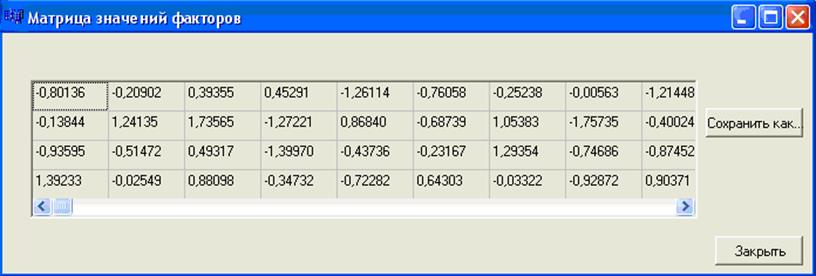
Рис.2.3. Матрица значений факторов.

3.4.  Выводы

Заключение

Разработано программное обеспечение, позволяющее проводить факторный анализ для разнотипных признаков, когда исходные данные представимы в различных шкалах

Исследования, проведенные на разработанном программном обеспечении