Факторный анализ

специфичность (b²_j) –        долю  дисперсии,   обусловленную   вариабельной спецификой признака X_j;

ненадежность (l²_j) –      долю дисперсии, обусловленную несовершенством измерений;

надежность (c²_j)–         долю дисперсии характерного фактора без учета ошибки, или дополнение дисперсии ошибки l²_j до полной дисперсии признака X_j.

Взаимосвязь показателей состава дисперсии элементарного признака X_jукладывается в общую схему (рис. 7.13):

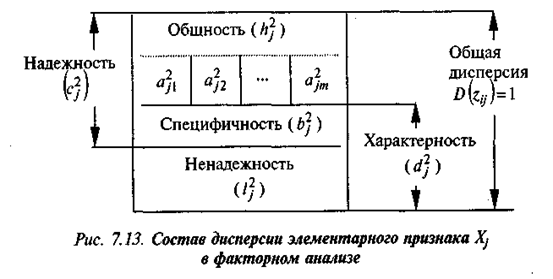
Рис. 7.13 позволяет установить алгебраические связи показателей состава дисперсии:

Соответственно уровню разложения дисперсии можно записать матричные линейные уравнения относительно элементарных признаков и воспроизведенной матрицы парных корреляций (R⁺):

Пример записи матричного уравнения R= АА' + U²в развернутом виде:

Вариант в), с полным расчленением дисперсии признака, используется достаточно редко, так как предполагает выполнение сложных алгоритмов вычислительных процедур.

Анализ состава дисперсии позволяет дополнить факторный анализ важными выводами о степени специфичности изучаемого явления и информативности статистических данных.

7.6. Метод главных факторов

Метод главных факторов можно рассматривать как развитие метода главных компонент. Основное отличие заключается в использовании редуцированной корреляционной матрицы R_h, на главной диагонали которой расположены уже не единицы, а характеристики общности h²_j.

Согласно классической модели факторного анализа, уравнение для определения коэффициентов при общих факторах F_rзаписывается в виде:

Z_j = a_j1F_l + a_j2F₂ +...+a_jmF_m+a_jD_i, или в матричной форме:

Z_j=AF+a_jD_j, где D_j– характерный фактор.

Решение уравнения при условии максимизации сумм:

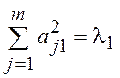          – первый максимум в части описанной дисперсии элементарных признаков (D(Z_j));

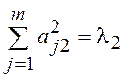         – второй максимум, относительно оставшейся после l₁

дисперсии и т.д, сводится к определению собственных значений и собственных векторов симметрической матрицы Rиз равенства (R-lE)U=0. В §7.4, посвященном методу главных компонент, показано, что при известных значениях l_j и U_jкоэффициенты a_jr можно рассчитать по формуле:

А = V×L^1/2,

где V— матрица нормированных векторов U_j:.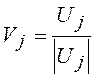

С учетом этого для вычислений a_jrвыводится общая формула:

.

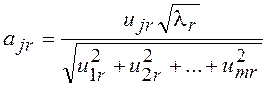В исследовательской практике существуют различные приемы, способы нахождения параметров модели главных факторов l, U_j, a_jr, условно их легко разделить на две большие группы. Первая группа ориентирована на алгоритм метода главных компонент и в сущности повторяет его, единственное отличие в том, что вычисления проводятся по данным редуцированной корреляционной матрицы, а не обычной матрицы парных корреляций. В этом случае сразу получают все т значений собственных чисел l_j и т собственных векторов. В факторном анализе, однако, такой подход используется редко, он считается менее адекватным традиционным целям факторного анализа и менее экономичным.

Во второй группе объединяются приемы, которые позволяют последовательно, начиная с первого, устанавливать значения собственных чисел и собственных векторов. Последующие шаги выполняются после предварительной проверки