Теория математического моделирования физических процессов. Исследование осциллятора.

Министерство Образования Российской Федерации

Новосибирский Государственный Технический Университет

Лабораторная работа №2

по курсу:

«Теория математического моделирования физических процессов»

Факультет: ПМИ

Группа: ПМ-03

Вариант: 1.2.4

Студентки: Настовьяк А.Е.

Тимощенко Т.В.

Преподаватель: Рудяк В.Я.

Новосибирск 2004

Условие задачи

Дана нелинейная колебательная система, описываемая уравнением:

                                        ,                                              (1)

Метод решения

Все расчёты и построение графиков проводилось в системе Maple . 

Была использована разностная схема вида: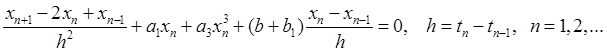 

Результаты

1.  Положив , определить параметр , при котором в системе возникает автоколебательный режим. Найти частоту этих колебаний. Построить соответствующее численное решение.

Уравнение принимает вид   

                                                                                                        (2)

-частота колебаний

Обозначим,

В системе возникнут автоколебания, если колебания (незатухающие) поддерживаются внешними источниками энергии.

То есть если в общем случае:

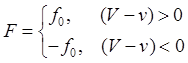
Таким образом, уравнение (2) перепишем в виде:

Тогда наше получившееся уравнение будет иметь решение в виде

,

-амплитуда колебания на n-м полупериоде.

Тогда производная (скорость) примет вид

  .

Подставим в начальные условия

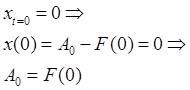
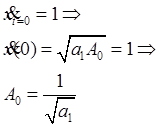
Значит,

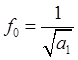
Соответственно, 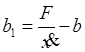 , и будем вычислять этот параметр численно. Будем сразу вычислять рассчитывать значение функции , которая будет меняться во времени, в зависимости от значения производной x.

Соответствующие численное решение примет вид:

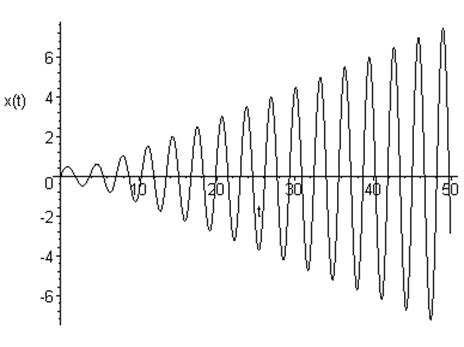
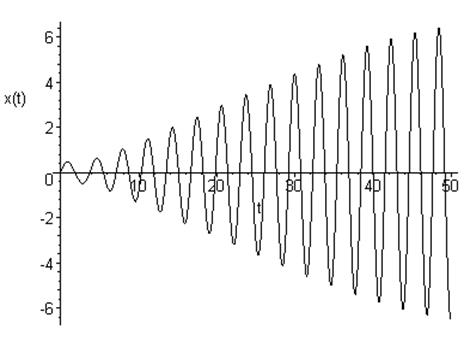
Видим, что движение осциллятора периодическое с растущей амплитудой колебания.

Фазовый портрет:

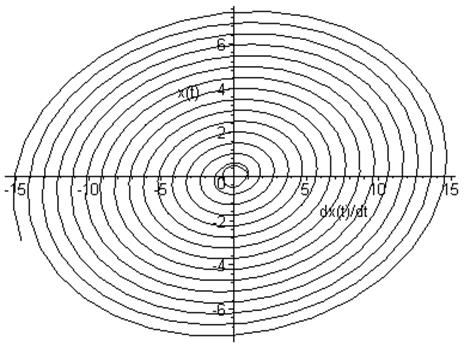
Траектория движения на фазовой плоскости имеет вид разворачивающейся спирали.

Движение осциллятора ускоряющееся.

2. Исследовать, как влияет на автоколебания нелинейность системы, т.е. изучить её решения  при в условиях автоколебательного режима.

Уравнение принимает вид (1) и . В условиях автоколебательного режима, построенных в предыдущем пункте мы можем наблюдать следующие:

Численное решение принимает вид:

Фазовый портрет:

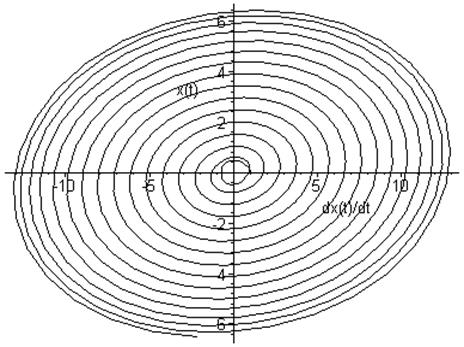
Таким образом, можем сказать, что при таком значении параметра при нелинейном члене уравнения не происходит  особых заметных изменений в движении осциллятора.

Однако попробуем ещё увеличить параметр до .

Получаем такие результаты

Численное решение:

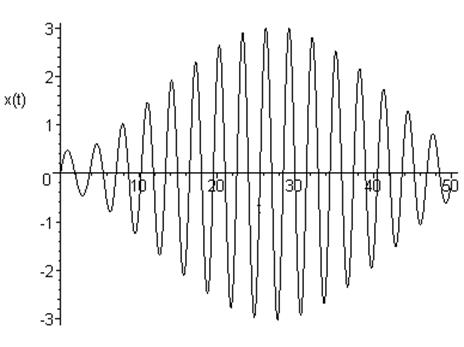
Фазовый портрет

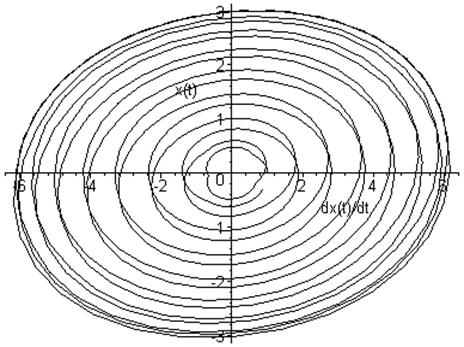
Таким образом, можем сказать, что нелинейность влияет на поведение осциллятора. Его движение становится ускоряющимся, но потом  колебания начинают затухать. Далее начинается новый период, и движение вновь ускоряется.

.