Лабораторная работа №2. Теория математического моделирования физических процессов

Министерство образования Российской Федерации

Новосибирский Государственный Технический Университет

Лабораторная работа №2

по курсу:

« Теория математического моделирования

физических процессов »

Факультет:         ПМИ

Группа:              ПМ-04

Преподаватель: Рудяк  В.Я.

Студентки:        Сайтгалин А.

Штабель Е.

Вариант:             2.6

Новосибирск 2004

Постановка задачи:

Дана нелинейная колебательная система, описываемая уравнением:

,

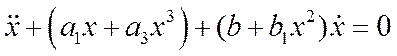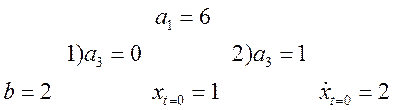
1.  Положив , определить параметр , при котором в системе возникает автоколебательный режим. Найти частоту этих колебаний. Построить соответствующее численное решение.

2.  Исследовать, как влияет на автоколебания нелинейность системы, т.е. изучить ее решения при  в условиях автоколебательного режима.

Методы расчетов:

В качестве языка программирования был выбран C++.

1.  При  , поиск  и

Ø Поиск  проводиться следующим методом:

  I.  Выбирается начальный интервал .

  II.  Далее пока , где - заданная точность решения,  вычисляется среднее 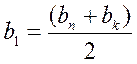, при котором проводиться решение поставленного уравнения.

  III.   Затем, если решение расходиться, то , иначе .

Ø Частота находиться через период:

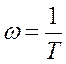
2.  Найденное значение подставлено в  и проделаны исследования.

Численное решение:

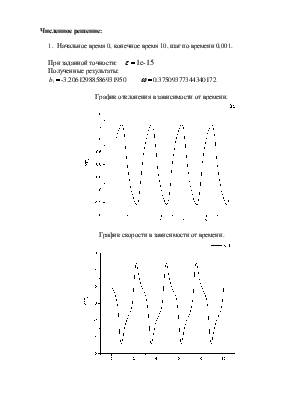
1.  Начальное время 0, конечное время 10, шаг по времени 0,001.

При заданной точности:       

Полученные результаты:

График отклонения в зависимости от времени.

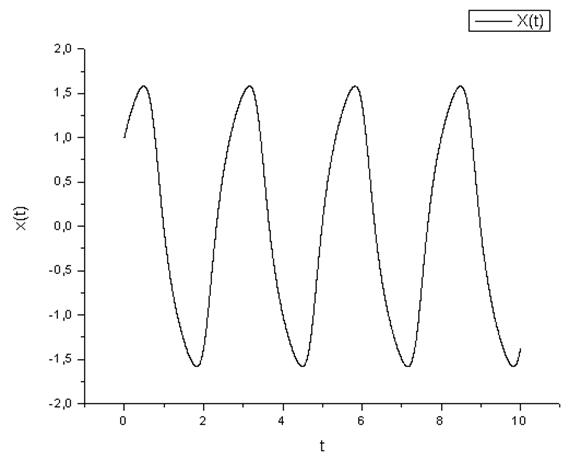
График скорости в зависимости от времени.

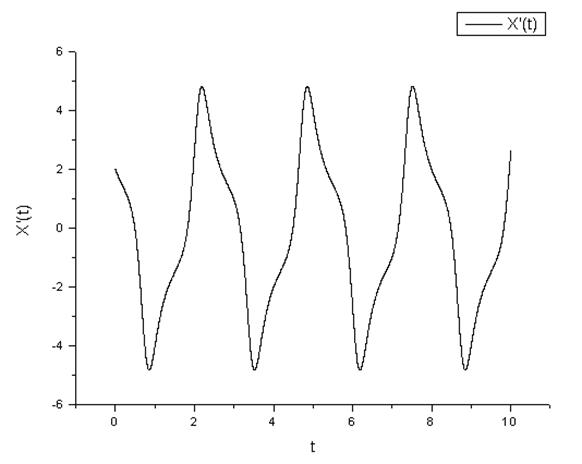
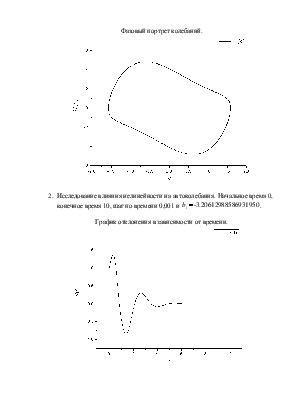
Фазовый портрет колебаний.

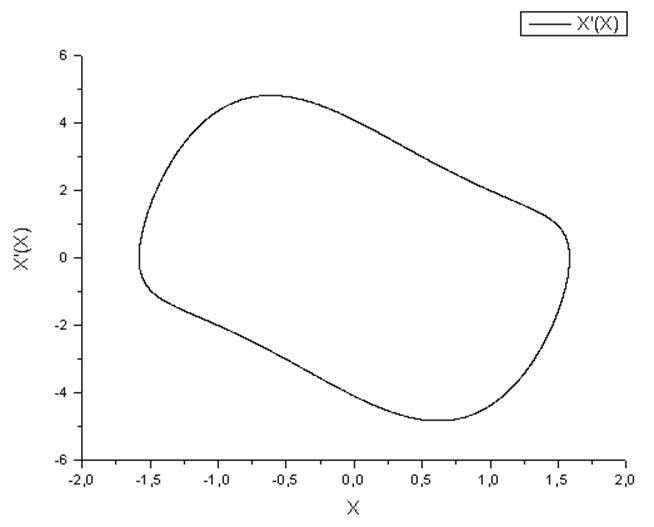
2.  Исследование влияния нелинейности на автоколебания. Начальное время 0, конечное время 10, шаг по времени 0,001 и .

График отклонения в зависимости от времени.

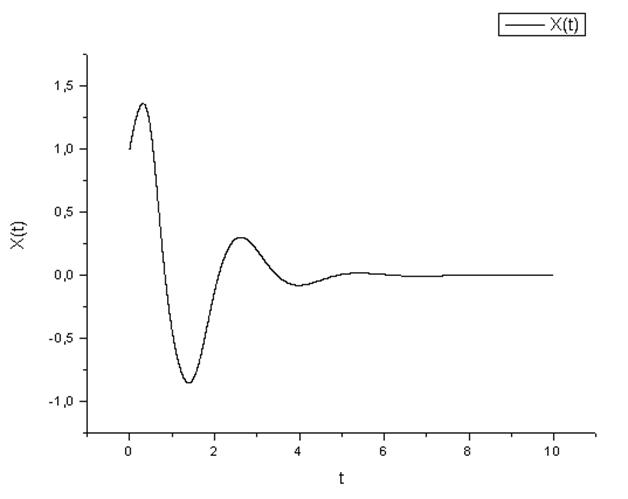
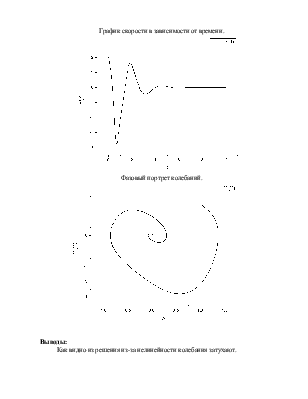
График скорости в зависимости от времени.

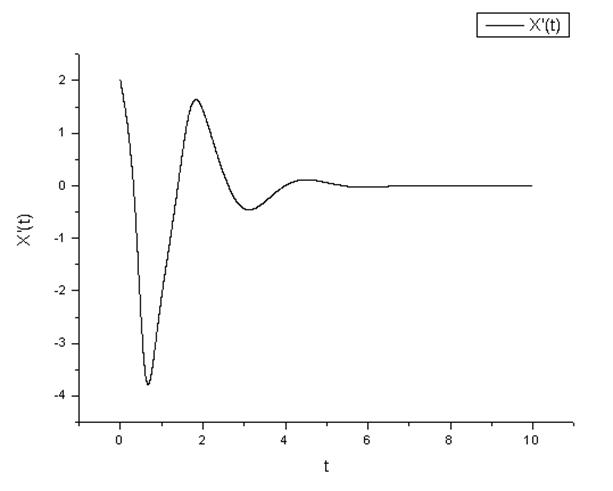
Фазовый портрет колебаний.

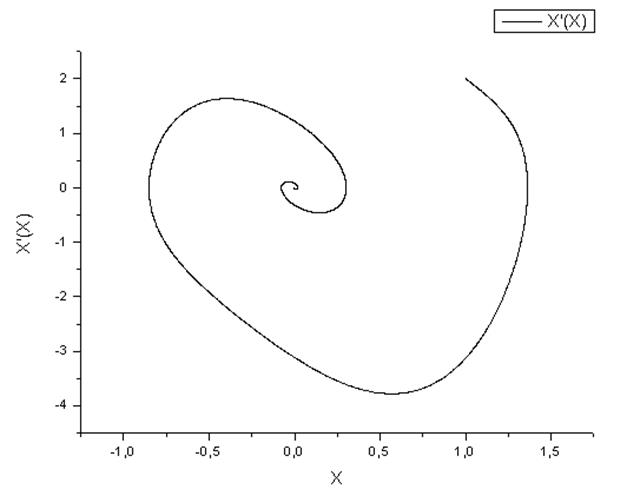
Выводы:

Как видно из решения из-за нелинейности колебания затухают.

Текст программы:

#include "stdio.h"

#include "stdlib.h"

#include "math.h"

#include <FLOAT.H>

//double a1=6,a3=1,b=2,b1=-3.20612988586931950;

double a1=6,a3=0,b=2,b1;

double bn=-3.5, bk=-3.0, Eps=1e-15;

double PI;

double f(double x,double x1,double t) {

return -a1*x-a3*x*x*x-(b+b1*x*x)*x1;

}

int Calc(double *t_,double *x,double *x1,double a,double b,double t0,double tk,double dt, double &p)

{

int i=0;

double k1,k2,t;

double xn1,xn,temp1,temp2,temp3;

double period=0, tSign, fl=0;

xn=a;

xn1=b;

t=t0;

while (t<tk) {

t_[i]=t;

x[i]=xn;

x1[i]=xn1;

temp1=xn;

temp2=xn1;

temp3=f(temp1,temp2,t);

xn=xn+xn1*dt+temp3*dt*dt/2.;

if (xn*temp1<0)

if (fl==0) {tSign=t; fl=1;} else

if (fl==1) {period=t-tSign; fl=2;}

k1=dt*temp3;

k2=dt*f(temp1,temp2+k1,t+dt);  

xn1=xn1+0.5*(k1+k2);

t+=dt;

i++;

}

p=2*period;

return i;

}

int main(int argc, char** argv)

{

int i, Count=0;

int n=20;

double *t,*X,*X1;

double t0=0,tk=10,dt=0.001;

double period;

n=(int)((tk-t0)/dt+20);

t=new double[n];

X=new double[n];

X1=new double[n];

//            n=Calc(t,X,X1,1.0,2.0,t0,tk,dt,period);

while ( bk-bn > Eps) {

b1=(bk+bn)/2.;

n=Calc(t,X,X1,1.0,2.0,t0,tk,dt,period);

if ( X[n-1]>=DBL_MAX || X[n-1]<=-DBL_MAX ) {

bn=b1;

}

else {

bk=b1;

}

}

printf("\n");

b1=(bk+bn)/2.;

//            printf("\nbn=%22.17lf bk=%22.17lf b1=%22.17lf\nChastota=%22.17lf\n", bn, bk, b1, 1./period);

printf("t           X            X1\n");

for (i=0;i<n;i++) {

printf("%lf   %lf    %lf\n",t[i],X[i],X1[i]);

}

delete[] t;

delete[] X;

delete[] X1;

return 0;

}