Теория математического моделирования физических процессов

Министерство Образования Российской Федерации

Новосибирский Государственный Технический Университет

Лабораторная работа №1

по курсу:

«Теория математического моделирования физических процессов»

Факультет: ПМИ

Группа: ПМ-03

Вариант: 1.1.5

Студентки: Настовьяк А.Е.

Тимощенко Т.В.

Преподаватель: Рудяк В.Я.

Новосибирск 2004

Условие задачи

Дана нелинейная колебательная система, описываемая уравнением:

,

Метод решения

Все расчёты и построение графиков проводилось в системе Maple . 

Была использована разностная схема вида: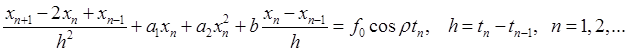 

Результаты

1. Определим частоту собственных линейных колебаний системы

Линейная колебательная система описывается уравнением ,  где  - частота собственных линейных колебаний, тогда в нашем случае  .

2. Исследуем линейный резонанс в системе, положив частоту вынужденных колебаний равной частоте собственных колебаний системы и : .

Решение данного уравнения будем искать в виде: , где  - разность искомого и вынужденного колебаний,  - амплитуда колебаний.

,

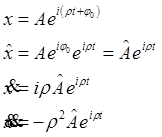Запишем исходное уравнение в виде:   , подставив в него выражения для , получим:

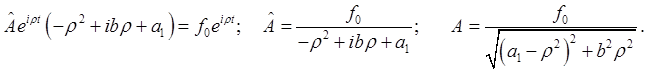
Положим частоту вынужденных колебаний равной частоте собственных колебаний системы, тогда уравнение для амплитуды примет вид:  .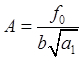

А вроде должно от времени зависеть и изменяться…..?

3. Построим аналитическое решение данного уравнения, считая : .

Решение этого уравнения будем искать в виде: , подставив это решение в уравнение, получим: 

, сгруппируем члены по порядкам малости:

.

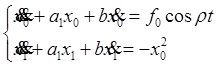Решение первого уравнения системы (получение ) будем представлять как сумму неоднородного частного решения и общего решения однородного уравнения.

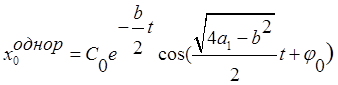
Подставляем  в первое уравнение системы:

Отсюда получаем:

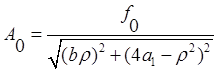
Сомнения по поводу А0…..?

Тогда получаем:

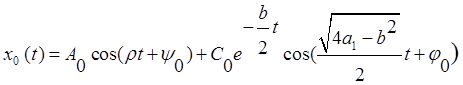
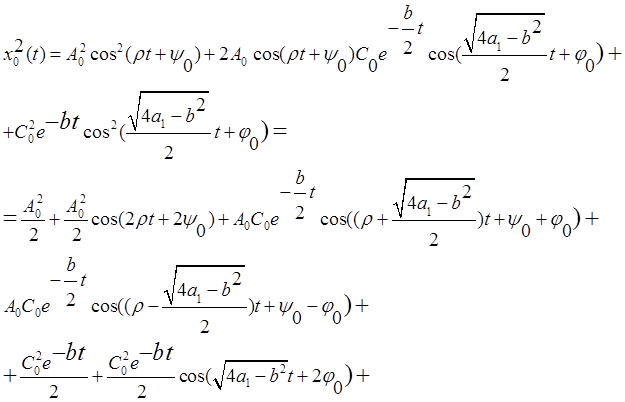
Подставим полученное значение для  во второе уравнение системы.

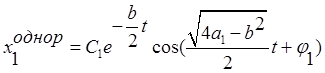
Теперь будем искать частные решения для каждого слагаемого.

Для первого слагаемого

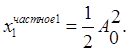
Для второго слагаемого

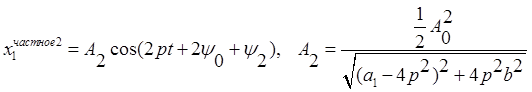
Для третьего слагаемого

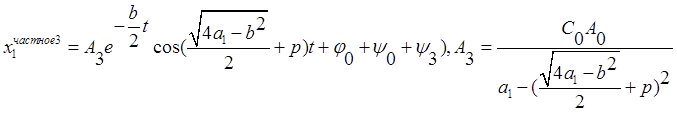
Для четвёртого слагаемого

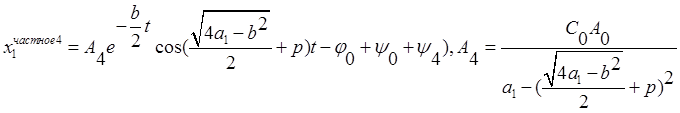
Для пятого слагаемого

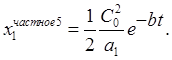
Для шестого слагаемого

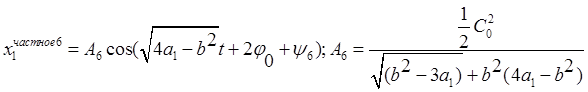
Таким образом, получаем решение

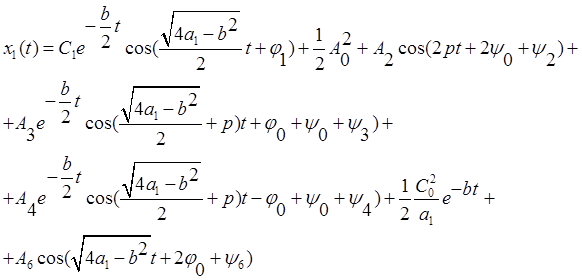
Тогда решение исходного уравнения примет вид:

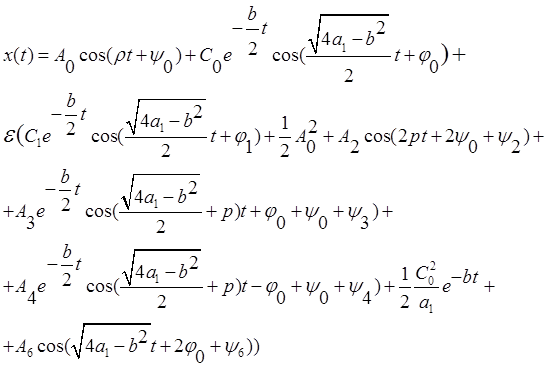
Коэффициенты  находятся из начальных данных: , а остальные коэффициенты выражаются через них:

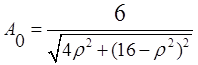
Какими будут эти коэффициенты и надо ли их считать(стр25)? Какая везде ро?

4. Построим аналитическое решение, соответствующее субгармоническому резонансу для случаев, когда  и

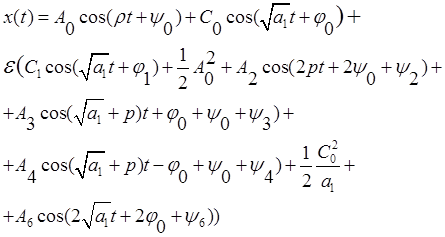
Появляются комбинационные частоты - супергармоники , равные удвоенной собственной частоте осциллятора. Поэтому, если на осциллятор действует сила с частотой равной половине собственной частоты линейного осциллятора, то в системе возникнет комбинационная частота , которая и окажется резонансной. Таким образом, резонанс, обусловленный действием на систему гармонической силы на субгармонической частоте( субгармонический резонанс), возможен при частоте .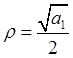

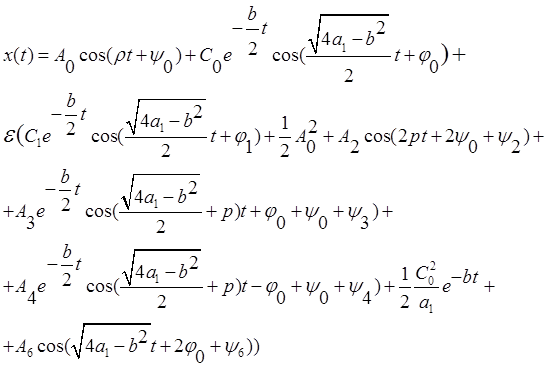
Субгармонического резонанса не будет.

5. Построим численное решение исходного уравнения

5.1. Случай

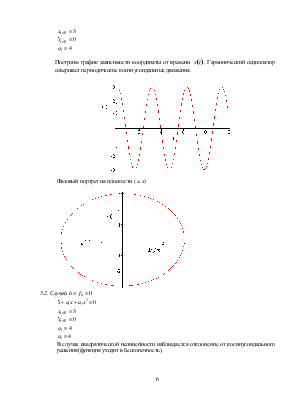
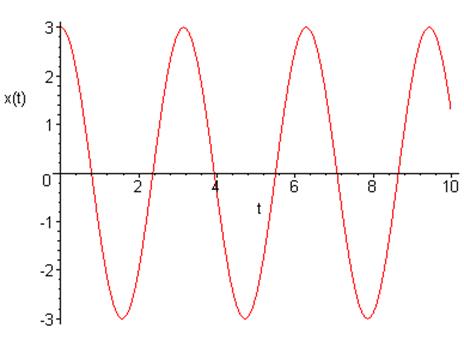
Построим график зависимости координаты от времени . Гармонический осциллятор совершает периодические косинусоидальные движения.

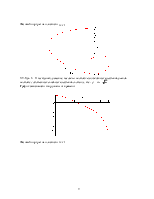
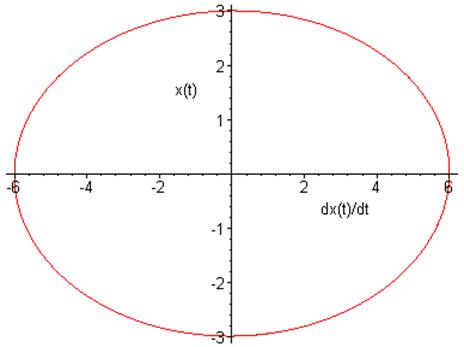
Фазовый портрет на плоскости

5.2. Случай

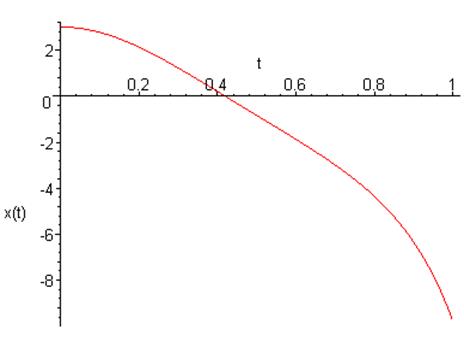
В случае квадратической нелинейности наблюдается отклонение от косинусоидального решения(функция уходит в бесконечность).

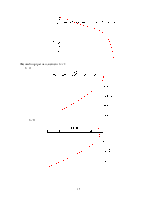
График зависимости координаты от времени:

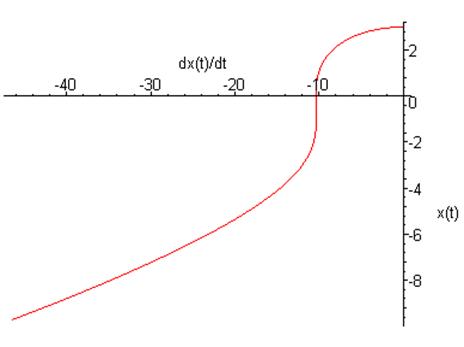
Фазовый портрет на плоскости

5.4. Случай

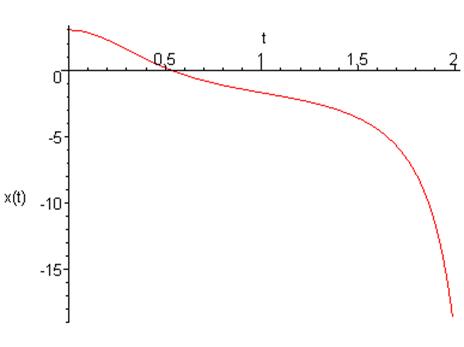
Ситуация аналогично предыдущему пункту. Наблюдается уход функции в бесконечность.

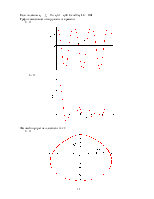
График зависимости координаты от времени:

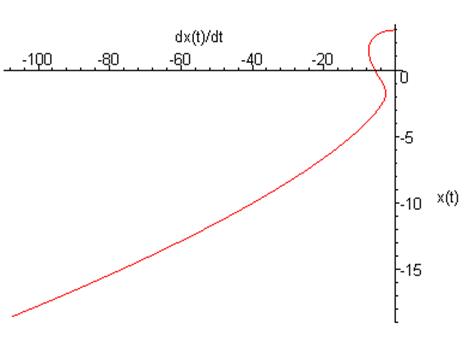
Фазовый портрет на плоскости

5.4. Полное решение уравнения

ро=0,1…???какое надо

График зависимости координаты от времени:

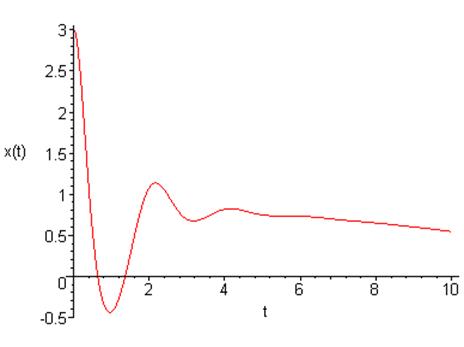
Фазовый портрет на плоскости

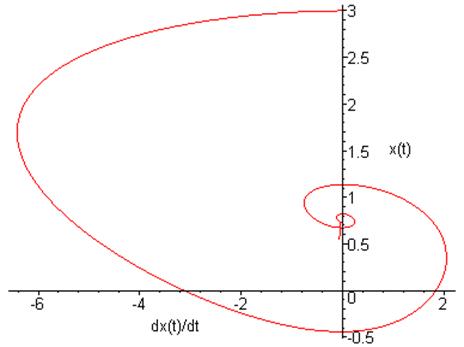
5.5. При  построить решение, положим частоту вынужденных колебаний равной частоте собственных линейных колебаний системы, т.е. 

График зависимости координаты от времени:

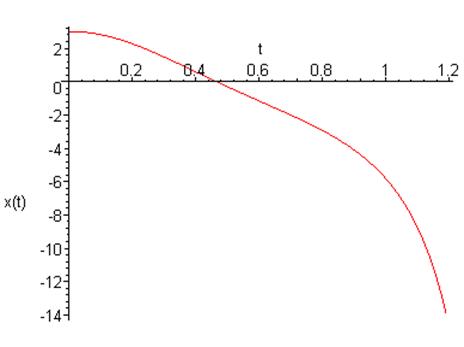
Фазовый портрет на плоскости

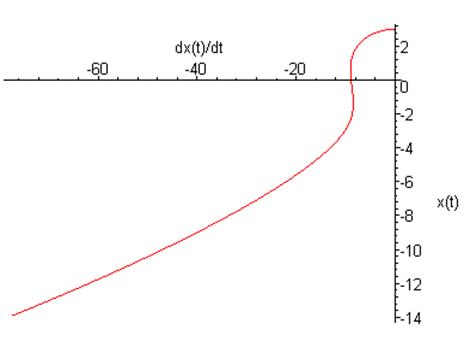
5.6. Для случая 5.5 изучить устойчивость решений относительно малых вариаций начальных данных

Будем изменять начальные данные и смотреть на поведение решения уравнения.

Пусть , т.е.

Получим следующую таблицу, где показана зависимость нормы вектора разности исходного и возмущённого решения от уровня зашумлённости.

Для некоторых случаев приведём графики.

График зависимости координаты от времени:

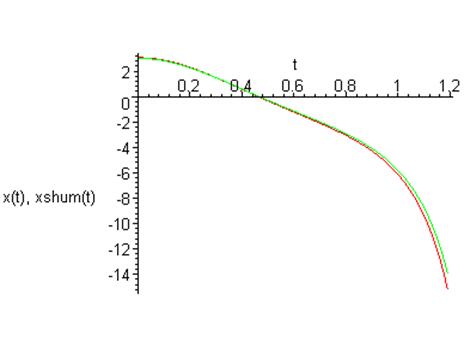
Фазовый портрет на плоскости

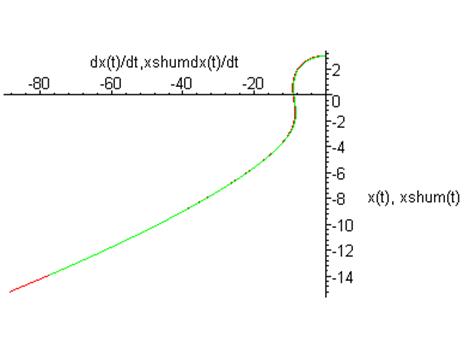
График зависимости координаты от времени:

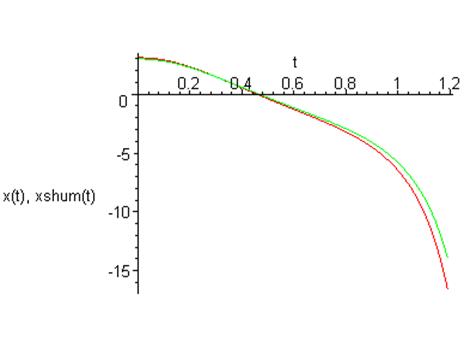
Фазовый портрет на плоскости

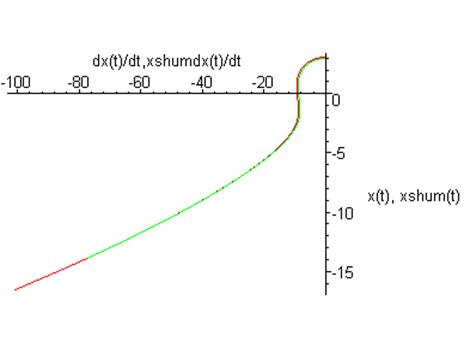
Мы видим, что при расстояние между двумя фазовыми траекториями растёт со временем, таким образом, решение не устойчиво относительно малых вариаций начальных данных.

Верно ли это….????

5.7 Для полного уравнения построить решение, положив частоту вынужденных колебаний равной частоте собственных линейных колебаний системы, т.е. 

График зависимости координаты от времени:

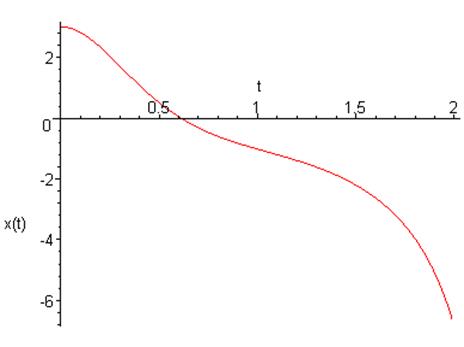
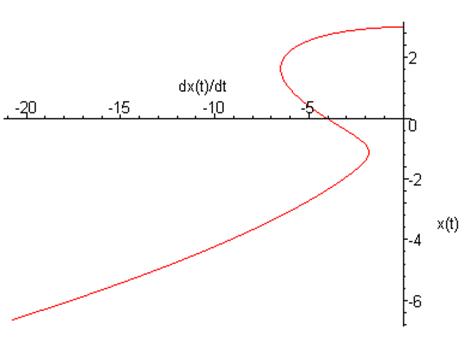
Фазовый портрет на плоскости

5.8. Определим,  при каком условии в исходном  уравнении появляется субгармонический резонанс. Построим соответствующее численное решение для случая, когда  и

Что будет при b<>0….?

Субгармонический резонанс возможен при частоте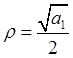

График зависимости координаты от времени:

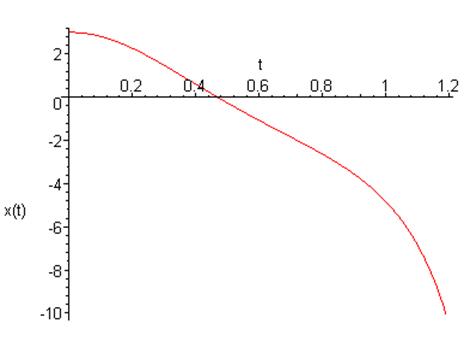
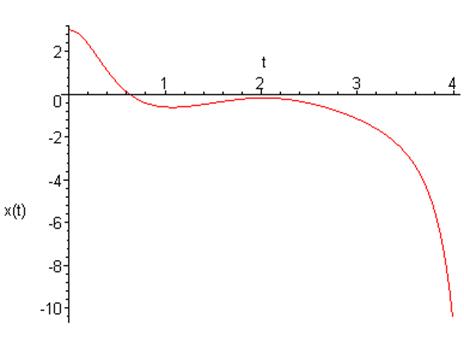
Фазовый портрет на плоскости :

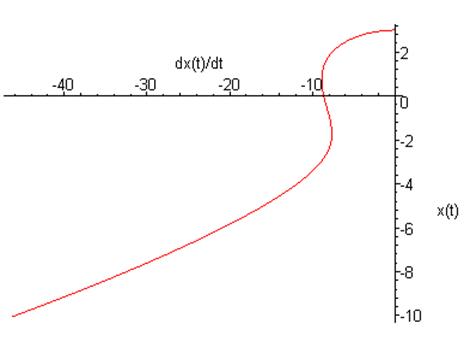
5.9. Определим,  при каком условии в системе может возникнуть параметрический резонанс. Построим соответствующее численное решение для случая, когда  и

Хрень какая-т!!!!!!!

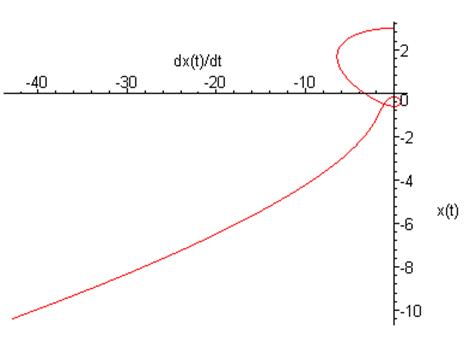
Параметрический резонанс возможен, если возьмём  вынуждающую силу на удвоенной частоте линейного осциллятора, получим:

График зависимости координаты от времени:

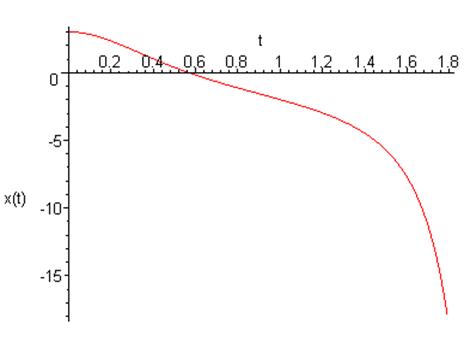
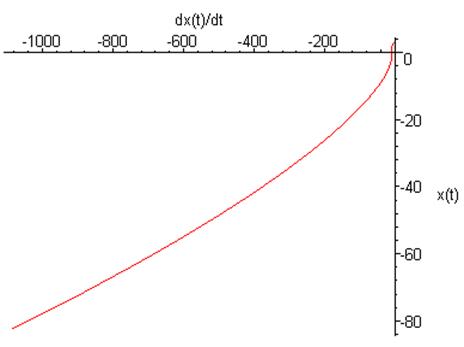
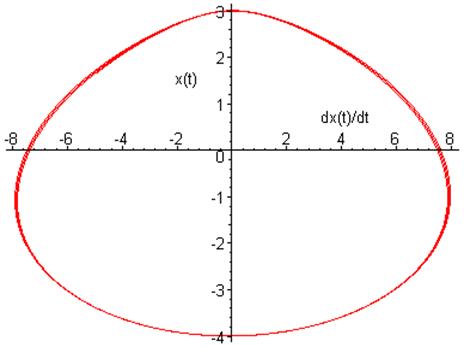
Фазовый портрет на плоскости :

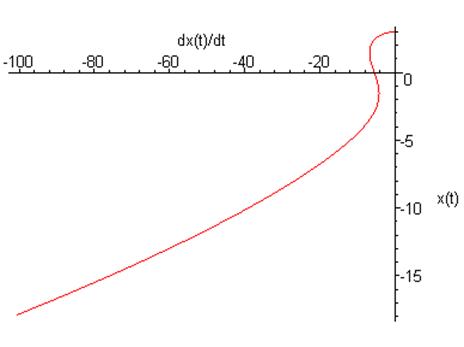
Если положим  и

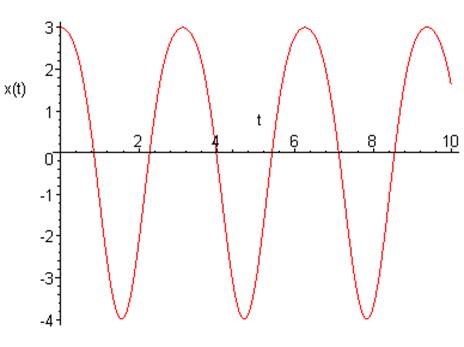
График зависимости координаты от времени:

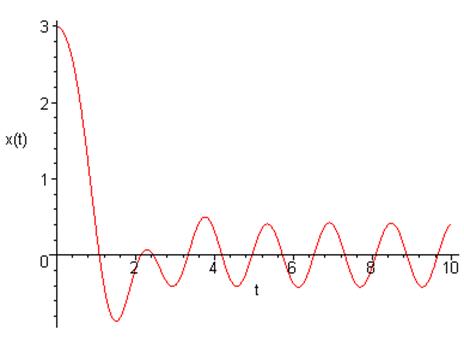
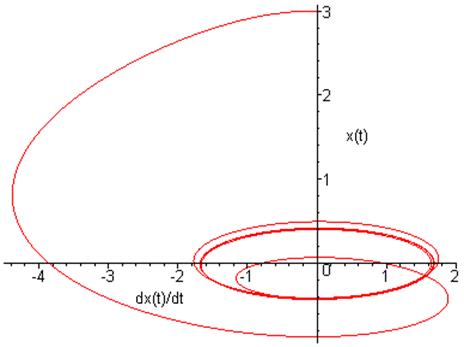
Фазовый портрет на плоскости :