Теория игр. Первый алгоритм Гомори

28) Первый алгоритм Гомори.

Все алгоритмы Гомори представляют собой реализацию метода отсечений. Дают правила построения отсечений.

Пусть (L^ц, C) — некоторая задача целочисленного программирования и опорный оптимальный план  соответствующей задачи линейного программирования не удовлетворяет условию целочисленности

.

Опр.   Неравенство

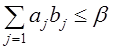(¬)       или 

называется правильным отсечением, если оно удовлетворяет следующим условиям:

I.  Условие отсечения.  не удовлетворяет правилу (¬), т.е.

.

II.  Условие правильности.  — план задачи (L^ц, C), то  удовлетворяет неравенству (¬), т.е.

Первый алгоритм Гомори предназначен для решения полностью целочисленных задач линейного программирования

(1)             

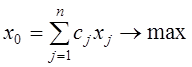
(2) 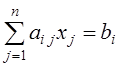            ,  i = 0, 1, 2, …, m,

(3)             x_j ³ 0, j = 0, 1, 2, …, n,

(4)             x_j ‑ целые, j = 0, 1, 2, …, n.

Пусть  — оптимальный опорный план задачи (L, C) (1‑3). Выразим целевую функцию L ₀ и все переменные x_j (jÎN), соответствующие оптимальному опорному плану .

(5) 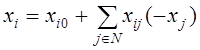                  ,                  i = 0, 1, 2, …, n.

Пусть x — вещественное число. Целой частью x называется наибольшее целое число, не превышающее x. Целая часть x обозначается [x]. Дробной частью x называется число

{x} = x ‑ [x].

Пример.

,       ,       .

Теорема. Пусть

(6)       1) 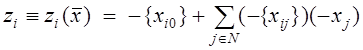       ,         i = 0, 1, 2, …, n;

2)         — план задачи  (L^ц, C)  (1‑4).

Тогда

(7)  z_i – целое

(8)                   z_i ³ 0.

Замечание. Если все c_j целые числа, то условия теоремы распространяются на случай i = 0.

Следствие. Пусть  не удовлетворяет условию целочисленности (4), так что для некоторого i (1 £ i £ n). x_i0 — нецелое.

Тогда соотношения (6), (8) задают правильное отсечение.

,

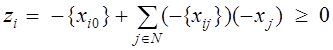z_i ³ 0.

Схема метода отсечений выглядит следующим образом. Имеется задача (1‑4) (L^ц, C).

На 0^ом этапе отыскивается оптимальный план задачи (L₀, C), которая получается отбрасыванием условия целочисленности .

Если этот план не является решением (L^ц, C), то строится правильное отсечение, отбрасывающее этот план и решается задача (L₁, C), на втором этапе (L₂, C) и т.д. … (L_r, C). Оптимальный план вспомогательной задачи линейного программирования (L_r, C) определяются неоднозначно, т.к. (L_r, C) может иметь много решений. Поэтому Гомори предложил вместо задачи (L_r, C) решать l‑задачу. l‑оптимальный план  определяется единственным образом.

Вычисления в методе Гомори проводятся в соответствии с l‑методом.

Основной проблемой при использовании методов отсечений является рост числа ограничений. Гомори предложил приём, ограничивающий размеры расширенных симплексных таблиц до

(n + 2)´(k + 1)

где n — количество переменных в (L₀, C), а k — число небазисных переменных в ней.

Этот приём основан на том, что дополнительные ограничения (прав. отсечения)

интересует нас не сами по себе, а только как способ отсечения нецелочисленного оптимума  и перехода от задачи (L_r, C) к задаче (L_r+1, C).

Переменная x_n+r+1 (r ³ 0) выводится из базиса сразу же после введения ограничения

x_n+r+1 ³ 0

.

Идея Гомори заключается в следующем:

а)    сразу же после вывода x_n+r+1 ³ 0 из базиса соответствующая строка вычёркивается из расширенной симплексной таблицы.

б)    Если в ходе дальнейших вычислений x_n+r+1 снова попадает в базис, то соответствующая строка  в симплексной таблице не восстанавливается и в дальнейших вычислениях x_n+r+1 не участвует.

Таким образом число столбцов в таблице не превышает k+1 (равно), а число строк — n+2, где n+1 строка соответствует x₀, x₁, …, x_n и одна x_n+r+1 в момент её включения.

Необходимо отметить, что алгоритм Гомори неприменим в следующих случаях:

Если задача (L, C) имеет решение, но не имеет решения l‑задача, т.е. множество оптимальных планов (L, C) не пусто, то и не ограничено.

Алгоритм (Блок‑схема).

Начальная итерация.

Решаем l‑задачу . Если она неразрешима, то и неразрешима и задача . Если  разрешима и l‑оптимальный план  удовлетворяет условию целочисленности,  является оптимальным планом задачи . Если  не удовлетворяет условию целочисленности, то переходим к общей итерации.

n^ая общая итерация (r³0).

Пусть  не удовлетворяет условию целочисленности. /Мы ищем нормальную и допустимую симплексную таблицу T_r = ||x_ij||, iÎQⁿ, .

Выберем наименьшую (по номеру) строку, которой соответствует нецелочисленная компонента

/Если целочисленность целевой функции гарантирована, то i = 1, 2, …, n/

и строится соответствующее правильное отсечение

      (¬)

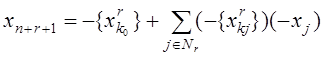x_n+r+1 ³ 0              x_n+r+1 — целое.

Строка приписывается снизу к таблице T_r. Получается недопустимая (только по строке x_n+r+1!) и l‑нормальная таблица, к которой применим l‑метод. Причём после вывода x_n+r+1 из базиса соответствующая строка вычёркивается, а после введения в базис