Теория игр. Задача распределения производственных мощностей

НГТУ

Лабораторная работа №1

по дисциплине «Теория игр»

Вариант 1

Факультет: ПМИ

Группа: ПМ-83

Студенты: Большакова А.В.

Журавлев В.А.

Миркин Е.П.

Переподаватели: Постовалов С.Н.

Тимофеев В.С.

г. Новосибирск, 2001

Условие задания: Плановое задание по изготовлению 4 видов костюмов необходимо распределить между 3 швейными фабриками. Производственные мощности i фабрики (i=1,2,3) позволяют за рассматриваемый период времени выпустить r(i,j) костюмов j модели (j=1,2,3,4). Заданы цены c(j) на костюм j модели и себестоимости s(i,j) изготовления j модели на i фабрике.

          

.

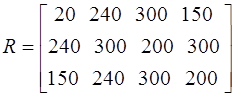
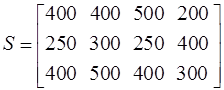
Плановое задание (180, 150, 100, 100).

Решить, опираясь на эти данные, следующие задачи и ответить на вопросы:

1.  Может ли быть выполнено плановое задание?

2.  Составить оптимальный план загрузки фабрик из условия минимизации себестоимости плановой продукции.

3.  Составить оптимальный план загрузки из условия максимизации прибыли при точном выполнении планового задания.

4.  То же, при допустимости перевыполнения планового задания.

5.  Составить оптимальный план загрузки фабрик, обеспечивающий  максимальное количество комплектов костюмов, если числа планового задания рассматривать как ассортиментные отношения.

Решение задач линейного программирования проводилось методом последовательного улучшения плана, при помощи программы-решателя lablp.exe

Математические модели и решения:

1.  Проверим возможность выполнения планового задания. Просуммировав по столбцу матрицу R, получим вектор [410, 780, 800, 650], каждая компонента  которого – это максимальное количество костюмов данного типа, которое может быть произведено всеми фабриками. Сравнив этот  вектор с плановым заданием, получаем, что плановое задание выполнимо.

2.  Пусть х₁ -  количество костюмов первого типа, произведенных первой фабрикой. х₂ -  количество костюмов второго типа, произведенных первой фабрикой.

х₃ -  количество костюмов третьего типа, произведенных первой фабрикой. х₄-  количество костюмов четвертого типа, произведенных первой фабрикой.

и т.д.

х₁₂-  количество костюмов четвертого типа, произведенных третьей                                фабрикой.

Тогда условие минимизации себестоимости можно записать как: 400х₁+250х₂+400х₃+400х₄+300х₅+500х₆+500х₇+250х₈+400х₉+200х₁₀+400х₁₁+ 300х₁₂ ® min.

При этом, учитывая, что i-я фабрика не может произвести костюмов j–го  типа больше чем r(i,j) получаем ограничения неравенства:

х₁£20                    х₄£240            х₇£300            х₁₀£150

х₂£240                  х₅£300            х₈£200            х₁₁£300

х₃£150                  х₆£240            х₉£300            х₁₂£200

Из условия точного выполнения плана следуют ограничения равенства:

х₁+х₂+х₃=180

х₄+х₅+х₆=150

х₇+х₈+х₉=100

х₁₀+х₁₁+х₁₂=100

Таким образом мы получили стандартную задачу линейного программирования.

Решение:

X_опт=(0,180,0,0,150,0,0,100,0,100,0,0)^т

т.е. для минимизации себестоимости, при точном выполнении планового задания требуется загрузить вторую фабрику на производство костюмов первого, второго и третьего типов, а первую фабрику – на производство костюмов четвертого типа.

3.  Так как плановое задание и цена на костюмы независимы от загрузки фабрик, то задача максимизации прибыли сводится к задаче минимизации себестоимости продукции, т.е. к пункту 2.

Решение:

Решение аналогично пункту 2 (см. математические модели).

X_опт=(0,180,0,0,150,0,0,100,0,100,0,0)^т

4.  Вводя переменные аналогично пункту 2, получаем условие максимизации прибыли, при допустимости перевыполнения плана:

(500*(х₁+х₂+х₃)-400х₁-250х₂-400х₃)+(650*(х₄+х₅+х₆)-400х₄-300х₅-500х₆)+

+(800*(х₇+х₈+х₉)-500х₇-250х₈-400х₉)+(500*(х₁₀+х₁₁+х₁₂)-200х₁₀-400х₁₁-                                                      300х₁₂) ® max        или

100х₁+250х₂+100х₃+250х₄+350х₅+150х₆+300х₇+550х₈+400х₉+300х₁₀+

+100х₁₁+200х₁₂ ® max при следующих ограничениях, следующих из производственных ограничений r(i,j):

х₁£20                    х₄£240            х₇£300            х₁₀£150

х₂£240                  х₅£300            х₈£200            х₁₁£300

х₃£150                  х₆£240            х₉£300            х₁₂£200

и ограничениях, следующих из допустимости перевыполнения плана:

х₁+х₂+х₃³180

х₄+х₅+х₆³150

х₇+х₈+х₉³100

х₁₀+х₁₁+х₁₂³100

Решение:

Х_опт=(20,240,150,240,300,240,300,200,300,150,300,200)^т т.е. максимальная прибыль, при допустимости перевыполнения плана, будет достигаться при полной загрузке всех фабрик по всем типам костюмов.

5.  Определение оптимального плана загрузки фабрик, обеспечивающего     максимальное количество комплектов костюмов, равноценно максимизации линейной формы:

  

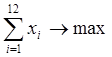
при производственных ограничениях:

х₁£20                    х₄£240            х₇£300            х₁₀£150

х₂£240                  х₅£300            х₈£200            х₁₁£300

х₃£150                  х₆£240            х₉£300            х₁₂£200

Воспользовавшись ассортиментным отношением, получим ограничения   равенства:

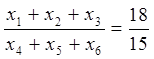
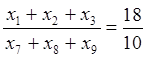
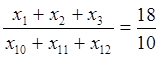              Þ

15*(х₁+х₂+х3)-18*(х₄+х₅+х₆)=0

10*(х₁+х₂+х₃)-18*(х₇+х₈+х₉)=0

10*(х₁+х₂+х₃)-18*(х₁₀+х₁₁+х₁₂)=0

Решение:

Х_опт=(20, 240, 150, 240, 101.666666, 0, 227.7777777, 0, 0, 150, 77.777777)^т.

т.к. количество костюмов не может быть дробным, округлим полученные значения:

Х^’_опт=(20, 240, 150, 240, 102, 0, 228, 0, 0, 150, 78)^т.

Проверим выполнение ассортиментных отношений:

 

     

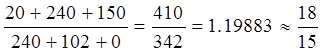
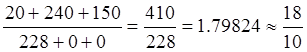
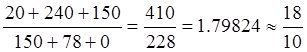
Выводы: