























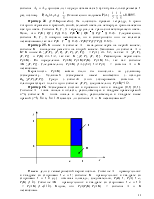



































наступление события А, произошло, знаем только, что событие А наступило), используется с целью уточнения вероятностей гипотез (меняется наше представление об условиях эксперимента).
Знаем,
что ![]() =
=![]() - использовали
формулы (1.5) и (1.6), k=1,…,n. С использованием формулы полной вероятности
(1.12) получаем:
- использовали
формулы (1.5) и (1.6), k=1,…,n. С использованием формулы полной вероятности
(1.12) получаем:
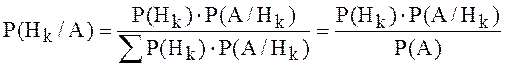 (1.13)
(1.13)
Полученная формула носит название формулы Байеса.
Для предыдущего примера P(H1/A)=P(H1) P(A/H1) / [P(H1) P(A/H1) + P(H2) P(A/H2)]=kр1/(k+1) / (kр1/(k+1) + р2/(k+1))=kр1/(kр1+р2), P(H2/A)=р2/(k+1) / (kр1/(k+1) + р2/(k+1))=р2/(kр1+р2). Если k=2, р1=0.15, р2=0.05, то априорные вероятности гипотез равны P(H1)=2/3, P(H2)=1/3, апостериорные вероятности после того, как покупатель приобрел бракованное изделие, равны P(H1/A)=2·0.1/(2·0.1+0.05)=4/5=0.8, P(H2/A)=0.05/0.25=0.2. Интерпретировать результат можно так: доля первого завода в браке составляет 0.8, что значительно больше половины и больше доли выпускаемой продукции (0.8 > 2/3). Видимо первому заводу стоит подумать о качестве выпускаемой продукции. Если он достигнет того же уровня брака, что и второй завод, то с очевидностью P(H1/A)=2/3, P(H2/A)=1/3. Если же 1 завод превзойдет 2 завод по качеству выпускаемой продукции, положим р1=0.03, то апостериорные вероятности примут значения P(H1/A)=3/8 и P(H2/A)=5/8, следовательно, теперь доля второго завода в браке чуть больше половины при объеме продукции в 2 раза меньшем, чем на 1 заводе. Теперь 2 заводу следует задуматься о качестве продукции. Можно решить такую задачу: какова должна быть величина р2, чтобы доля 2 завода в браке была < 1/3? Решаем ее при р1=0.03: P(H2/A)=р2/(kр1+р2) < 1/3 ó р2/(0.2+р2) < 1/3 ó р2 < 0.02.
Пример 28. На 4 карточках написаны буквы в, к, л, о. Карточки перемешиваются и выкладываются в ряд. Какова вероятность, что получится слово “волк” - событие А.
Имеем
схему урн, в урне 4 шара; вынимаются все шары. Выборка без
возвращения, упорядоченная. Число m=n,
следовательно, по таблице 1 имеем |Ω|=А![]() =n!=4!=24.
Слово “волк” образует только одна перестановка, следовательно,
Р(А)=1/24.
=n!=4!=24.
Слово “волк” образует только одна перестановка, следовательно,
Р(А)=1/24.
Пример 29. Из колоды в 36 карт наудачу вынимается 3 карты. Какова вероятность, что все они будут одной масти - событие А?
Имеем дело с неупорядоченной выборкой без возвращения. Следовательно
|Ω|=С![]() =36·35·34/1·2·3. Найдем число э.
событий, благоприятствующих событию А (составляющих событие А).
Зафиксируем определенную масть. Чтобы имело место событие А в выборку
должны попасть любые 3 карты этой масти. Опять имеем дело с неупорядоченной выборкой без возвращения, следовательно, n
=36·35·34/1·2·3. Найдем число э.
событий, благоприятствующих событию А (составляющих событие А).
Зафиксируем определенную масть. Чтобы имело место событие А в выборку
должны попасть любые 3 карты этой масти. Опять имеем дело с неупорядоченной выборкой без возвращения, следовательно, n![]() =C
=C![]() (в колоде карт одной масти 9 штук). В задаче речь идет не
об определенной масти, а о любой из 4, следовательно,
(в колоде карт одной масти 9 штук). В задаче речь идет не
об определенной масти, а о любой из 4, следовательно,
![]() . Таким образом,
. Таким образом, 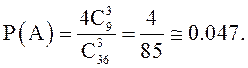
Пример 30. Какова вероятность герою «Пиковой дамы» выиграть?
В колоде, видимо, 56 карт. Германн выигрывает, если в
первый вечер из колоды вынимает «тройку», во второй – «семерку» и в третий –
туза. Масть роли не играет. Следовательно, 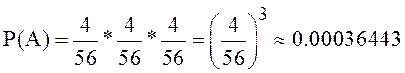 или,
если свести вычисления к схеме урн, имеем выборку по 3 элемента из 56
упорядоченную с возвращением, следовательно
или,
если свести вычисления к схеме урн, имеем выборку по 3 элемента из 56
упорядоченную с возвращением, следовательно![]() . Число
элементарных событий, благоприятствующих событию А, находим по такой схеме:
число троек, семерок, тузов в колоде поровну – 4. Поскольку масть карт роли не
играет, мы можем считать число n
. Число
элементарных событий, благоприятствующих событию А, находим по такой схеме:
число троек, семерок, тузов в колоде поровну – 4. Поскольку масть карт роли не
играет, мы можем считать число n![]() равным n
равным n![]() =С
=С![]() С
С![]() С
С![]() . Следовательно,
. Следовательно, 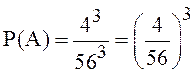 .
.
Пример 31. Предположим, что n неразличимых частиц распределяются по m ячейкам. Ограничений на число частиц в ячейке нет. Событие А – в фиксированную ячейку попало ровно k частиц.
Термин «неразличимые частицы» предполагает, что различными будут такие распределения частиц по ячейкам, которые отличаются только числом частиц в ячейках. Здесь также можно применить схему урн, но с шарами двух различных видов в ней. Пусть частицы – это белые шары, перегородки между ячейками – черные шары.
|
|
↔ |
|
Эксперимент состоит в том, что из урны последовательно
вынимаются все шары. Рассматриваем, как в последовательности шаров размещены
черные шары. На приведенном выше рисунке, читаемом в обратном порядке, видим,
что последовательность вынутых шаров имеет вид бчбббччббббчч... Следовательно,
в первую ячейку попала 1 частица, во вторую – 3 частицы, в третью – ни одной, в
четвертую – 4 и т. д.. ![]() совпадет с числом всевозможных
размещений (m-1) черных шаров среди n+m-1 шаров обоих
цветов, это число равно
совпадет с числом всевозможных
размещений (m-1) черных шаров среди n+m-1 шаров обоих
цветов, это число равно ![]() . Если в фиксированную
ячейку попадает k частиц, то оставшиеся n-k частиц
размещаются по m-1 ячейкам произвольным образом, число
таких размещений равно
. Если в фиксированную
ячейку попадает k частиц, то оставшиеся n-k частиц
размещаются по m-1 ячейкам произвольным образом, число
таких размещений равно ![]() . Следовательно,
. Следовательно, 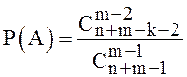 . Такое размещение частиц по ячейкам носит
в физике название статистики Бозе-Эйнштейна. Ей подчиняются фотоны,
атомные ядра, атомы с четным числом частиц.
. Такое размещение частиц по ячейкам носит
в физике название статистики Бозе-Эйнштейна. Ей подчиняются фотоны,
атомные ядра, атомы с четным числом частиц.
Пример 32. Рассмотрим ту же ситуацию, что и в
примере 31, только на число частиц в ячейке имеется ограничение – в каждой
ячейке может находиться не более одной частицы. Здесь предполагается m ![]() n.
Событие А – занято k фиксированных ячеек.
n.
Событие А – занято k фиксированных ячеек.
Эта схема размещения ассоциируется со схемой выборки из урны
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.