Теоретические данные для экзамена по теории искусственного интеллекта

отрицание могут быть выведены из исходных посылок, то методом полного перебора всегда можно получить искомое доказательство через конечное число шагов.

Метод решения задач, использующий аппарат логики предикатов, основан на представлении задачи в виде теоремы: формула F логически следует из множество формул Ф0 (Ф0 =>F). Доказательство этой теоремы состоит в том, чтобы показать, что каждая интерпретация, удовлетворяющая Ф0, удовлетворяет и F, или, что то же самое, Ф1 = Ф0  невыполнимо. Обычно используют второй путь, то есть доказывается, что Ф1 невыполнимо (метод доказательства от противного).

8.Принцип резолюции.

1.  принцип силлогизма в ИВ, т.е. для формул в которых нет переменных (A È B) & (^ØA È C) -> (B È C)

2. принцип подстановки – это принцип отыскания частных случаев "x₁,…,x_n  F(x₁,…, x_n) -> F(t₁,…,t_n),т.е. высказывание получаем из предположения, подставляя термы и делая это предложение тем самым истинным.

Из двух предложений можно получить резольвенту (их следствие) след. образом:

1)переменные одного предложения переименовывается так, чтобы они отличались от переменных второго предложения, т.е. переменные делаются уникальными.

2)Находится подстановка, при которой какой-либо дизъюнкт одного предложения становится дополнительным к дизъюнкту второго предложения и эта подстановка производится в оба предложения.

3)На основе принципа силлогизма эти два дизъюнкта вычеркиваются.

4)Если имеются одинаковые дизъюнкты в предложении, то все они кроме одного вычеркиваются на основании свойства идемпотентности: F & F & … &F -> F

5)Оставшееся предложение – резольвента

Фактор (следствие из предложения) можно получить следующим образом:

1)  находится подстановка, при которой какие-либо дизъюнкты одинаковые: все одинаковые дизъюнкты кроме одного вычеркиваются.

2)  полученное предложение – фактор

Принцип резолюции позволяет переходить к более частным предложениям и более простым.

9.Доказательство теорем с помощью принципа резолюции. Теорема Робинсона.

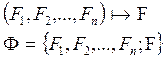                  этапы доказательства невыполнимости:

0.  введем отображение R⁽⁰⁾, где (0) – степень отображения – это суперпозиция 

1. 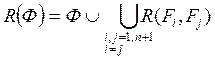 , где  - это резольвента для ;   

2.    и так далее…

k. 

Если - невыполнимо, то - также невыполнимо, то есть сохраняется свойство инвариантности для невыполнимости.

Справедливо обратное утверждение.

Вывод:  если  - невыполнимо, то  такое конечное , что  содержит пустое предположение (тождественно – ложное предположение). Последнее возможно, если в  имеются такие два предложения , которые после применения к ним соответствующей подстановки приводится к виду .   - тождественно – ложное предположение, если  - тождественно – ложно.

В основе Пролога лежит механизм доказательства теоремы, основанный на резолюции.

Теорема Робинсона. Если конечное множество предложений – невыполнимо, то опровержение может быть получено за конечное число применений принципа резолюций.

Вывод: 1. принцип резолюции является полным в смысле теоремы Робинсона (полным в  том смысле, что всегда получим решение); 2. принцип резолюции – непротиворечив (всегда  путь, который приводит к такому преобразованию, которое дает конечный результат)

10.Стратегии вывода с использованием резолюции. Стратегия упрощения.

Множество предложений упрощают, исключая из него некоторые предложения или из его предложений некоторые литералы. Такие упрощения позволяют снизить скорость роста числа новых предложений. Предложение можно исключить, если оно содержит уникальный литерал, т.е. литерал, не входящий с отрицанием ни в одно из предложений. Упрощения должны быть такими, чтобы упрощенное множество предложений было невыполнимо тогда и только тогда, когда невыполнимо исходное множество.

Стратегии упрощения:

а)           Стратегия исключения тавтологий;

б)           Стратегия исключения предложений, содержащих уникальный литерал