Статистические методы. Моделирование регрессионного процесса с гетероскедастическим возмущением

Условие задачи

1.  Провести моделирование регрессионного процесса с гетероскедастическим возмущением: дисперсия возмущений – возрастающая функция от расстояния точи до центра эксперимента.

2.  Полученные данные проверить по тестам на наличие гетероскедастичности.

3.  Провести оценивание параметров регрессионной модели по обобщенному МНК и по обыкновенному МНК.

4.  Сравнить эффективность оценок МНК и ОМНК.

Анализ задачи

1. Обобщенный МНК

В случае процесса с гетероскедастическим возмущением имеем, что дисперсии различных наблюдений не равны друг другу, т.е.

var (e_i) ¹ var (e_j), i¹j

В этом случае var (e) = s²W = diag (s₁², s₂², …, s_n²) = V.

Тогда V^–1 = diag (, ,…, )

Тогда 

2. Проверка данных на гетероскедастичность.

2.1. Тест Брейнча-Пагана

1.  Формулируем гипотезу о гомоскедастичности модели: a₁ = a₂ =…=a_p = 0.

2.  Считаем ошибку e = y – f^T(x)q.

3.  Оцениваем дисперсию: = .

4.  Вводим новый отклик`y = 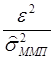 и рассчитываем для этого отклика остаточную сумму квадратов RSS.

5.   Если гипотеза справедлива, то ½ RSS Î

2.2. Тест Гольдфельда-Квандтона

1.  Формируем гипотезу о гомоскедастичности: a₁ = a₂ =…=a_p = 0.

2.  Выбираем некоторое количество N_c наблюдений, которые нужно отбросить из середины выборки (чаще всего N_c = ).

3.  Оцениваем регрессию на левой и правой частях выборки, считаем RSS₁ и RSS₂. Вычисляем отношение .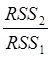

4.  Если гипотеза о гомоскедастичности не отвергается, то <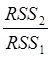

3. Эффективность оценок

® min

Программа решения задачи

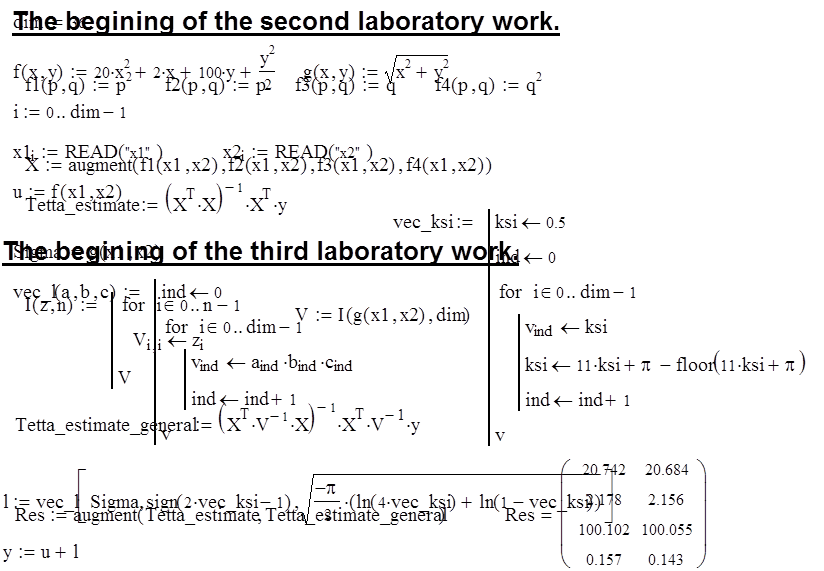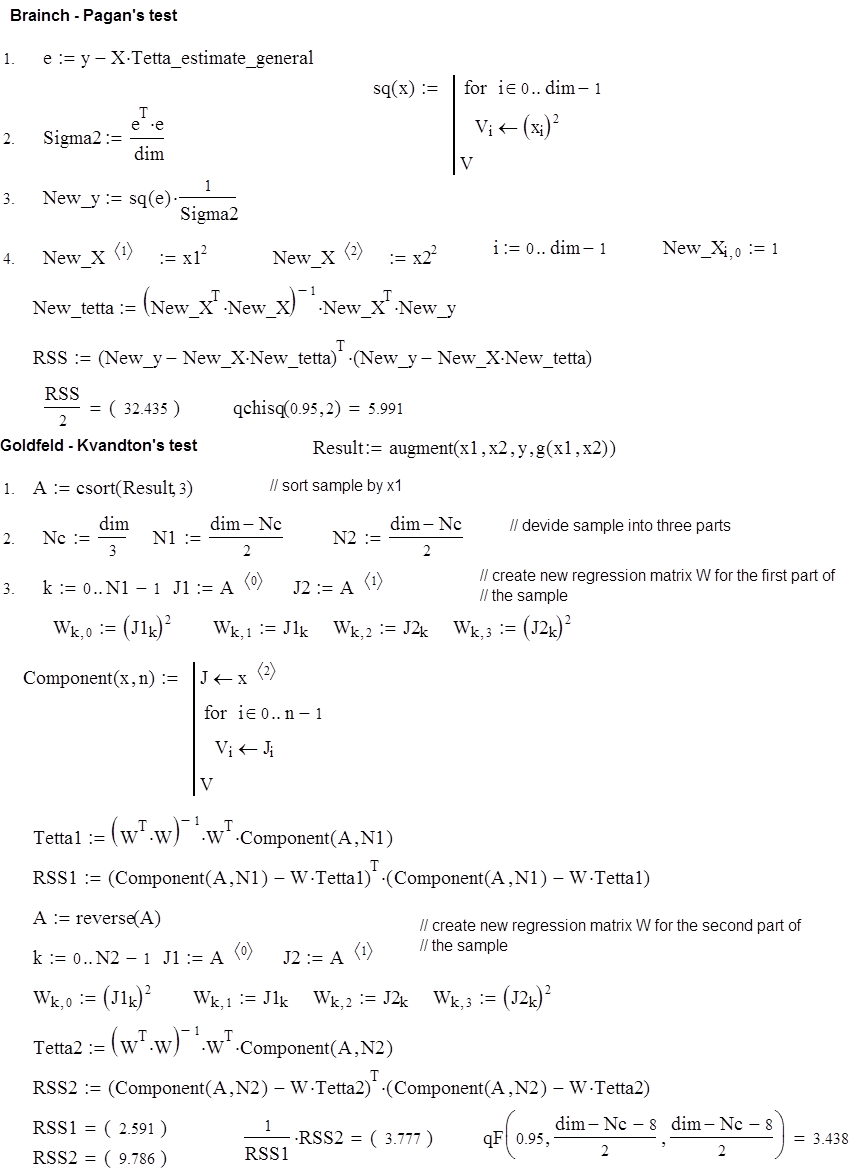Результаты:

1.  Тесты Брейнча-Пагана и Гольдфельда-Квандтона показали, что гипотеза о гомоскедастичности отвергается, т.к. ½ RSS Ï  ( 32,435 > 5,991 ) и 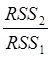 >  ( 3.777 > 3.438 ).

2.  Поскольку  < , то значит, оценка, полученная по обобщенному МНК, является эффективнее, чем оценка, полученная по обычному МНК.