



Министерство Образования Российской Федерации
кафедра прикладной математики
Факультет: ПМИ
Группа: ПМ-91
Студент: Кучеров Д.А.
Преподаватель: Цой Е.Б.
2003
Задание 1.
Составить алгоритм моделирования случайного вектора ![]() , имеющего в области
, имеющего в области ![]() распределение f(x1,x2).
распределение f(x1,x2).
Решение.
![]() .
.
Определим константу C из
условия, что 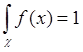 . Таким образом, С=3/2.
Данную задачу можно перевести из декартовой системы в полярную систему. Тогда
удобно моделировать полярные координаты, а уже по ним вычислять
. Таким образом, С=3/2.
Данную задачу можно перевести из декартовой системы в полярную систему. Тогда
удобно моделировать полярные координаты, а уже по ним вычислять ![]() . Сделаем замену переменных и найдем
якобиан преобразования:
. Сделаем замену переменных и найдем
якобиан преобразования:
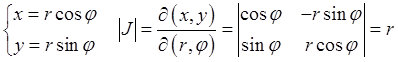 .
.
Тогда 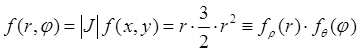 . При этом плотности независимых случайных
величин
. При этом плотности независимых случайных
величин ![]() и
и ![]() , имеют
вид:
, имеют
вид: ![]() и
и 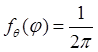 , где
, где ![]() и
и ![]() . Теперь
воспользуемся методом обратной функции для моделирования
. Теперь
воспользуемся методом обратной функции для моделирования ![]() и
и ![]() .
.
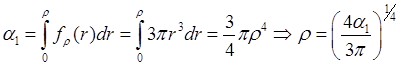
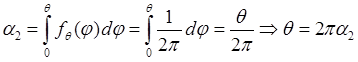
Следовательно, 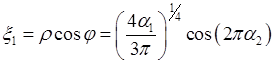 и
и 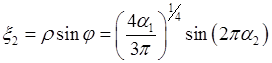 Составить алгоритм моделирования случайного
вектора
Составить алгоритм моделирования случайного
вектора ![]() `, имеющего в
области
`, имеющего в
области ![]() распределение f(x1,x2
,x3).
распределение f(x1,x2
,x3).
Задание 2.
Составить алгоритм моделирования случайного вектора ![]() , имеющего в области
, имеющего в области ![]() распределение f(x1,x2),
по методу исключения.
распределение f(x1,x2),
по методу исключения.
Решение.
![]()
Определим константу C из
условия, что 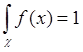 . Таким образом, С=
. Таким образом, С=![]() . В качестве функции g(x,y)
можно взять константу
. В качестве функции g(x,y)
можно взять константу ![]() .
. 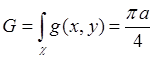 .
Тогда алгоритм можно записать следующим образом:
.
Тогда алгоритм можно записать следующим образом:
1. моделируем
![]() с плотностью
с плотностью ![]() и
значение
и
значение ![]() ;
;
2. если ![]() , то идем на 1 и так далее, иначе
, то идем на 1 и так далее, иначе ![]() .
.
Задание 3.
Найти моделирующее выражение для нормального
случайного вектора ![]() с дисперсионной матрицей K и математическим ожиданием m.
с дисперсионной матрицей K и математическим ожиданием m.
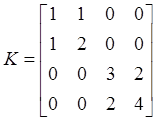
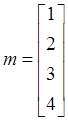
Решение.
Моделировать новую случайную величину будем с
помощью следующего линейного преобразования: ![]() .
Предположим, что A является треугольной матрицей
вида:
.
Предположим, что A является треугольной матрицей
вида:
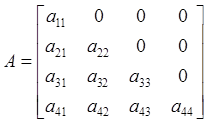
Коэффициенты матрицы A можно найти при помощи рекуррентной процедуры.
![]()
![]()
![]()
![]() , где
, где ![]() .
.
![]()
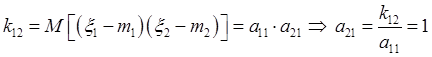
![]()
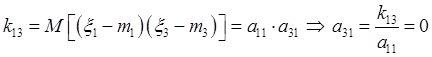
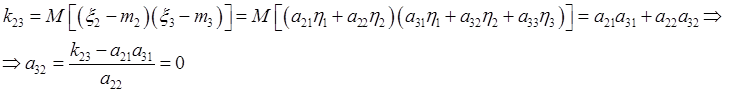
![]()
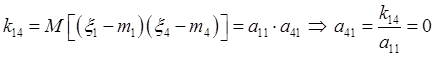
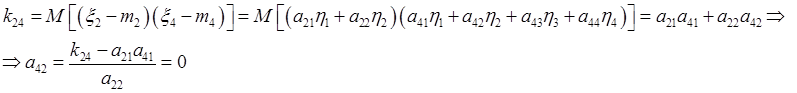
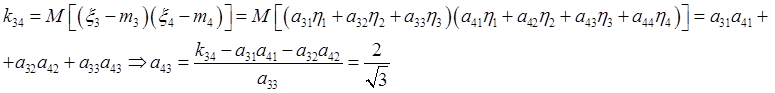
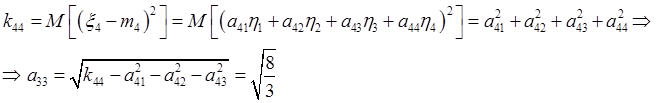
В результате можно выписать окончательное моделирующее выражение:
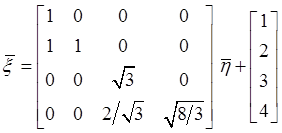
![]() .
.
Задание 4.
Написать алгоритм моделирования одномерного
стационарного гауссовского марковского процесса с нулевым априорным средним и
одномерной корреляционной функцией вида: ![]() .
.
Решение.
Найдем условное математическое ожидание m(t|y(s)) и дисперсию K(t|y(s)): ![]()
![]() .
.
Таким образом, значения процесса ![]() можно вычислить по рекуррентной формуле:
можно вычислить по рекуррентной формуле:
![]()
![]() , где
, где ![]() -
независимые, нормально распределенные величины с нулевым средним и единичной
дисперсией.
-
независимые, нормально распределенные величины с нулевым средним и единичной
дисперсией.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.