



Министерство образования и науки Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра прикладной математики и информатики
Моделирование и управление в экономике
Группа: ПМ-15
Студент: Кичаева Н. А.
Преподаватель: Цой Е.Б.
Новосибирск
2005
Задание
№1: Составить алгоритм моделирования случайного
вектора ![]() , имеющего в области
, имеющего в области ![]() распределение
распределение ![]() .
.
Решение:
Пусть![]() ,
, ![]() .
.
Константу
найдем из условия нормировки: 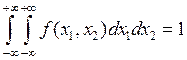 .
.
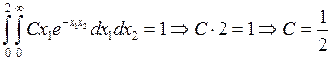 .Тогда
.Тогда 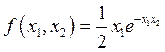 .
.
a)
![]()
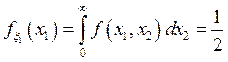 ,
, ![]()
![]() ,
, ![]()
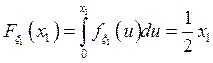
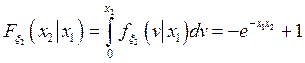
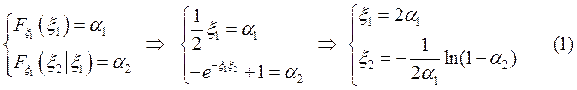
b)
![]()
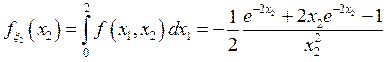 ,
, ![]()
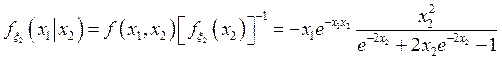 ,
, ![]()
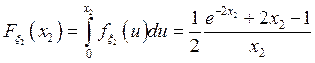
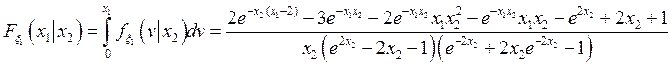
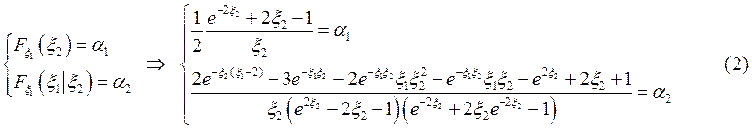
Алгоритм
моделирования случайного вектора![]() :
:
1.Генерируем
случайные величины ![]()
2.Находим
искомый случайный вектор ![]() , решая систему (1) или
(2).
, решая систему (1) или
(2).
Задание
№2: Составить алгоритм моделирования случайного
вектора ![]() , имеющего в области
, имеющего в области ![]() распределение
распределение ![]() , по методу исключения.
, по методу исключения.
Решение:
Пусть![]() ,
, ![]() .
.
Постоянную ![]() найдем из условия
нормировки
найдем из условия
нормировки 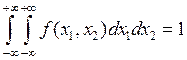 :
:
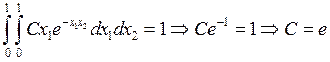 ,
тогда
,
тогда ![]() .
.
Далее,
пусть ![]() , соответственно
, соответственно
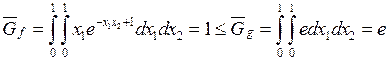 .
.
Алгоритм
моделирования вектора ![]() с плотностью
с плотностью 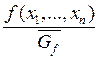 выглядит
следующим образом:
выглядит
следующим образом:
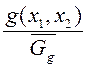 , и получаем величину
, и получаем величину Задание
№3: Найти моделирующее выражение для нормального
случайного вектора ![]() с дисперсионной матрицей K и математическим ожиданием m.
с дисперсионной матрицей K и математическим ожиданием m.
Решение:
Пусть
дисперсионная матрица 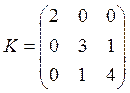 и вектор мат.ожидания
и вектор мат.ожидания 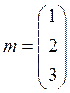 .
.
Для многомерного вектора, распределенного нормально, функция плотности распределения имеет вид:
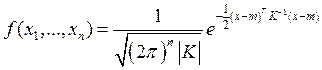 .
.
Пусть
имеем совокупность ![]() ,тогда
,тогда ![]() .
.
Полагая,
что ![]() является нижнетреугольной матрицей,
запишем общую рекуррентную формулу для вычисления ее элементов:
является нижнетреугольной матрицей,
запишем общую рекуррентную формулу для вычисления ее элементов: 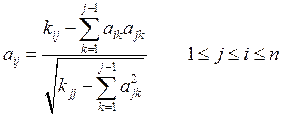 .
.
Вычислим матрицу ![]() :
:
![]()
![]()
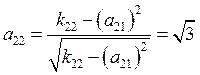
![]()
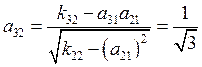
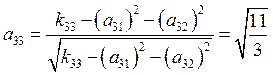
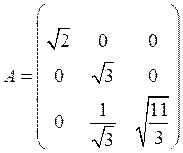 , тогда моделирующее выражение
для нормального случайного вектора
, тогда моделирующее выражение
для нормального случайного вектора ![]() имеет вид:
имеет вид:  .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.