Случайные эксперименты. Случайные события

алгебра  А – это  класс  ω-множеств,  замкнутый  относительно  счетного  числа  арифметических  операций.

Вероятностью  события  А  называется  величина  Р(А)=m/n.

Тройка  объектов (Ω,  А,  Р )  называется  вероятностным  пространством. 

Вероятность,  заданную  на  σ-алгебре  А,  называют  вероятностной  мерой.

Вероятность  события  А  при  условии,  что  в  опыте  произошло  событие  В,  называют  условной  вероятностью,  обозначают  ее  символом  Р(А/В). 

События  А  и  В  называются  независимыми,  если  Р(АВ)=Р(А) Р(В).                

Случайной величиной называется измеримая функция ξ, ставящая в соответствие каждому элементарному исходу  число .

Функцией распределения (вероятностей) случайной величины ξ называется функция , значение которой в точке x равно вероятности события .

Случайная величина ξ называется дискретной, если она каждому элементарному исходу ставит в соответствие одно число и из конечного или счётного множества чисел.

Если по ней функцию распределения  возможно восстановить однозначно, то такая характеристика называется законом распределения случайной величины.

Непрерывной случайной величиной называется случайная величина, функция распределения которой F(x) представима в виде интеграла 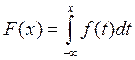. Функцию f(x) называют плотностью распределения.

Отображение  , задаваемое совокупностью случайных величин  , называется случайным вектором.

Назовем условной функцией распределения  случайной величины  при условии условную вероятность события  при условии события .

Случайные величины  называются независимыми, если имеет место равенство            

Математическим ожиданием случайной величины  называется число

 Дисперсией с. величины x называют числоDx = M (x - Mx)²                       

Начальным моментом порядка c. величины называется число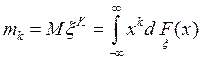       

Центральным моментом порядка  c. величины называется число= 

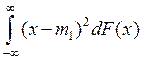
Условным математическим ожиданием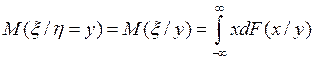    

Ковариацией с. величин x и h называют математическое ожидание произведения центрированных с. величин и:

Коэффициентом корреляции с. величин x  и h называют число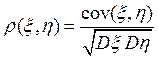  

Асимметрией с. величины x называется число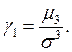

Эксцессом с. величины x называется число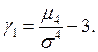

Характеристической функцией  с. величины  называется функция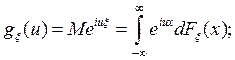

Аксиоматическое  определение  вероятности

Р1:   Р(А) ≥ 0   "Ає А  -  аксиома  неотрицательности;

Р2:   Р(Ω) = 1  -   аксиома  нормированности;

Р3:   Если  A_iA_j=Ø,  i ≠ j,  то  Р( U_kA_k )=Σ_k=1P(A_k)  -  аддитивность  сложения.

Свойства  вероятности.

1). Р(Ø) = 0.

2.  Р(Ā)=1 – Р(А).

3). Если  А  В,  то  Р(А) ≤ Р(В).

4). Р(А) ≤ 1.

5).  Р(АUB) = P(A) + P(B) – P(AB)  -  формула  вероятности  суммы  событий

6).  Р(АUB) ≤ P(A)+P(B),

7). Р(U_k=1A_k)=Σ_k=1P(A_k) – Σ_{i,j i<j}P(A_iA_j)+…+(-1)^n-1P(A₁A₂…A_n).

8). Р(U_n=1A_n) ≤ Σ_n=1P(A_n).

9). Если  {A_n}  монотонная  последовательность  событий  и  А= lim_n→∞A_n= {U_n=1A_n,  если  A_n+1A_n,  n ≥ 1;  ∩_n=1A_n,  если  A_n+1  A_n,  n ≥ 1,  то  Р(А)= lim_n→∞Р(A_n).

Основные свойства функции распределения.

F1.

F2. F(x) – неубывающая функция, т. е. если , то .

F3.

F4. F(x) – непрерывная слева функция.

F5. .

Простейшие свойства плотности распределения.

1. f(x )≥0
2. 

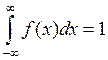
3.  

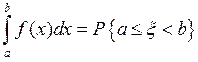
Свойства совместной функции распределения

5. для всего множества перестановок чисел 1,2,…,n.

6.Если m<n, то .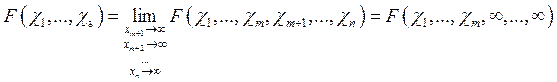

7.Справедливо соотношение

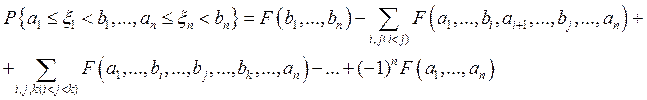
При n=2 формула принимает вид

Свойства совместной плотности распределения

1.

2.

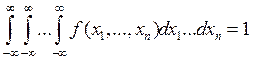
3. Если , то

4. Условие согласованности: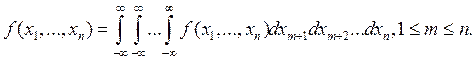

Свойства математического ожидания.

М1. , если С-const. Для С ,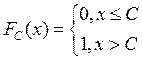

M2.

М3.

М4. , если   - независимые случайные величины.

М5. Если с вероятностью 1 , то

М6.

Свойства дисперсии.

Д1).   если

Д2)           

Д3). Если величины независимы, то .

Следствия.   

Д4).          

Свойства условного математического ожидания.

5.  M[ M(x½h)]=Mx  Следствие.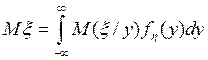  

6.  , h и j – некоторые функции

7.  M(x½h) = Mx,, если x и h - независимы.

Ковариация с. величин обладает следующими свойствами:

1. cov(x,,x) = Dx

2. Если x и h независимы, то cov(x,,h) = 0 

3.Пусть.Тогда.

4. 

5.

6..

Свойства r:

1.   r(x ,x) =1

2.   Если x  и h независимы, то  r(x ,h) = 0

3.  Пусть . Тогда .

4.  r(x,,h) = ± 1, тогда и только тогда, когда с. величины x, и h линейно зависимы.

5.

Некоторые свойства характеристических функций.

1.

2. Если h = ax+b,то 

3. Пустьи – независимые с. величины и .Тогда

4. Если существует начальный момент порядка N,  то характеристическая функция с.     величины дифференцируема N раз, при этом  

5.  Характеристическая функция g(u) – равномерно непрерывная функция.

Теорема 1 (Бореля - Кантелли). Если  - последовательность независимых событий, то

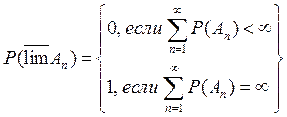
Теорема 3.  Пусть x – неотрицательная с. величина с вероятностью 1 и существует . Тогда 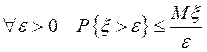      - Неравенство Чебышева

1. События равновероятны Р(А)=m/n, Р(А)= μ(А)/μ(Ω).

2.  Шары                                                                                                                                                         

3. Условная вероятность Р(А/В) = Р(АВ) / Р(В)    

4. Полная вероятность      Р(А)=Σ Р(H_k) P(A/H_k)               

5. Формула Байеса  P(H_k/A) = P(H_k) P(A/H_k)  /  Σ P(H_k) P(A/H_k)   

6. Бернулли: вероятность P(n,m) наступления m успехов в серии из n независимых испытаний, если успех в каждом отдельном испытании наступает с вероятностью p, равна

7. Пуассона: Если число испытаний в схеме Бернулли n велико, вероятность успеха в одном испытании p мала и мало также число , тогда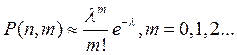             

8. Муавра – Лапласа. Если в схеме Бернулли число испытаний – n велико, то для всех m справедливо приближенное равенство

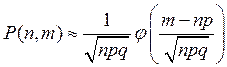, где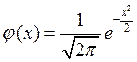                         

Вероятность того, что число успехов μ заключено в границах от m₁ до m₂ , приближенно равна

                                  где ,

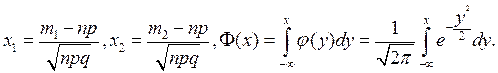Интеграл 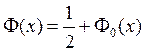 , где  – интеграл Лапласа,  .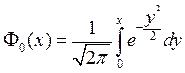         

9. Функцию распределения дискретной случайной величины можно записать в виде

9.1. Биномиальное распределение ξ –  число успехов в серии из n независимых испытаний.

 , где   

9.2. Геометрическое распределение ξ – число испытаний, которое необходимо провести, прежде чем появится первый успех.

9.3. Пуассоновское распределение ξ распределена по закону Пуассона, если