Случайные события

ячейкам носит в физике название статистики Бозе-Эйнштейна. Ей подчиняются фотоны, атомные ядра, атомы с четным числом частиц.

Пример 32.  Рассмотрим ту же ситуацию, что и в примере 31, только на число частиц в ячейке имеется ограничение – в каждой ячейке может находиться  не более одной частицы. Здесь предполагается m  n. Событие А – занято k фиксированных ячеек.

Эта схема размещения ассоциируется со схемой выборки из урны с m шарами n шаров. Выборка без возвращения, неупорядоченная.  Тогда согласно таблице 1 . На самом деле, исходами опыта могут быть такие последовательности: первые n ячеек заняты частицами, остальные свободны;

первые (n-1) ячеек заняты частицами, n-ая ячейка свободна, (n+1) ячейка занята

и т. д. . Число таких последовательностей совпадает с числом размещений из m элементов по n. Когда в каждой из k фиксированных ячеек будет по частице, остальные n-k частицы распределятся по оставшимся  m-k ячейкам по тому же принципу, как в задаче 31. Следовательно, ,  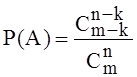  .    Такое распределение частиц по ячейкам носит название статистики Ферми- Дирака, ей подчиняются электроны, протоны, нейтроны.

            Пример 33. Условия задачи, как и в примере 31, но частицы различные. На число частиц в ячейке ограничений нет. Каждая из  n различных частиц может попасть в каждую из m различных ячеек. Событие А: в первую ячейку попало n₁ частиц, во вторую ячейку попало n₂ частиц, …, в m ячейку попало n_m частиц, n₁+n₂+…+n_m=n.

Условие размещение частиц предполагает, что если обратиться к схеме урн, то каждый из n различных шаров может попасть в выборку на любое место в ней. Следовательно, имеем дело с выборкой с возвращением. Размещение по ячейкам отличается одно от другого не только тем, сколько частиц в ячейке, но и какие частицы в ячейке (об этом говорит условие, что частицы различные), следовательно, выборка упорядоченная. Тогда . Число элементарных событий, благоприятствующих событию А, равно 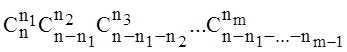. Это значит, в первую ячейку попали любые n₁ частиц из n, при этом порядок выбора частиц несущественен. Как только ячейка заполнена, остается  n-n₁ частиц, из которых во вторую ячейку могут попасть любые  n₂ частиц и т.д. Тогда

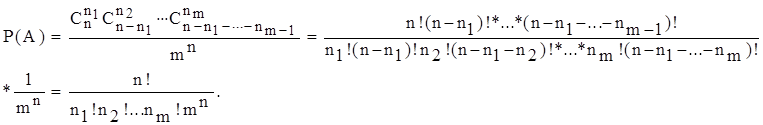
Такое распределение частиц носит название статистики Максвелла-Больцмана, ей подчиняется идеальный газ.

            Пример 34. Пусть имеется n частиц, из которых n₁ – одного типа, n₂- второго,…, n_k – k-ого типа, n=n₁+n₂+…+n_k. Случайным образом из них выбирается m частиц, m ≤ n. Событие А – в выборку попало m₁ частиц первого типа, m₂ частиц – второго типа, … ,  m_k частиц k-ого типа,  m=m₁+m₂+…+m_k .

Выборка без возвращения, неупорядоченная, следовательно,   ,

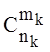m₁ частиц из n₁ мы можем выбрать способами, …, m_k частиц из n_k -  способами. При этом любой способ выбора частиц одного типа коммутирует с любыми способами выбора частиц остальных типов, т. е. 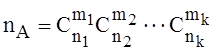. Тогда 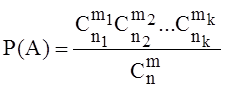. Если число P(A) обозначить как  P(m₁, m₂, … ,m_k) – тем самым мы указываем на зависимость события А от чисел ,, - и просчитать вероятности всех таких событий, то получим множество вероятностей , которое носит название гипергеометрического распределения. Частный случай этого распределения при к=2 рассмотрен в примере 12.

1.11  Схема Бернулли

Схемой Бернулли (или последовательностью независимых одинаковых испытаний, или биномиальной схемой испытаний) называют эксперимент, удовлетворяющий условиям: 1) за основу берется эксперимент, имеющий 2 исхода. Это может быть , например, появление некоторого события В  - один исход, и не появление этого события В – другой исход: 2) этот исходный эксперимент повторяется независимо n раз. Термин «независимо» означает, что исходы эксперимента при очередном повторении не зависят от исходов эксперимента на предыдущих шагах; 3)  вероятности двух исходов при  каждом повторении исходного эксперимента одни и те же.

Итак, пусть в случайном испытании событие B появляется с вероятностью p и не появляется с вероятностью 1-p=q. Проводится серия таких независимых испытаний. Элементарными исходами опыта тогда будут последовательности вида .Сопоставляя буквам B и буквы У и Н соответственно, можно элементарные исходы представить в виде