Испытывается устройство, состоящее из 4 независимо работающих приборов. Вероятности отказа приборов таковы: р1=0.3, р2=0.4, р3=0.5, р4=0.6. Найти математическое ожидание и дисперсию числа отказавших приборов.
(1,8; 0.94)
53. Дисперсия каждой из 9 одинаково распределенных независимых с.величин равна 36. Найти дисперсию среднего арифметического этих величин.
54. Распределение с. величины x определяется формулами р{x=i}=1/5, i=0,±1,±2. Найти распределение величин -x и |x|.
55. Распределение случайной величины x определяется формулами P{x=k}=c/k(k+1), k=1,2,... Найти а) с; б) P{x≤3}; в)P{h1≤x≤h2}.
56. Плотность распределения с. величины x задается формулами Px(x)=c/x4, если х³1 и Рx(х)=0, если х<1. Найти: а) с; б) плотность распределения с. величины h=1/x; в)Р{0.1<h<0.3}.
57. С.величина имеет показательное распределение с параметром a. Найти плотности распределений с.величин а) h=√x; б) h=x2; в) h=1/2lnx; г) h={x}; д) h=1-e-ax.
58. С.величина распределена равномерно на отрезке [0,1]. Найти плотность распределения с.величины а)h=2x+1; б) h=-ln(1-x).
59. С.точка В имеет равномерное распределение на окружности x2+(y-a)2=r2, а с.точка С=(x,0) является пересечением оси абсцисс с прямой, проходящей через центр окружности и точку В. Найти функцию распределения и плотность распределения с.величины x (распределение Коши).
60. С.величина x имеет непрерывную функцию распределения F(x). Показать, что с.величина h=F(x) имеет равномерное распределение на [0,1].
61. Пусть x равномерно распределена на [0,1], a F-1(y)=sup{x:F(x)<y}, 0≤y≤1, функция, обратная к функции распределения (не обязательно непрерывной ). Доказать, что с.величина x=F-1(h) имеет функцию распределения F(x).
62. Функция F(х) непрерывна в каждой точке. Доказать, что она равномерна непрерывна на R.
![]() 63. Совместное распределение с.величины x1,x2 дается
числами р11=1/8, р12=1/12, р13=7/24, р21=5/24,
р22=1/6, р23=1/8, где Рij=Р{x1=xi,x2=yi}, i=1,2; j=1,3, x1=-1,x2=-1; y1=-1, y2=0, y3=1. Найти
а) одномерное распределение Рx1, Рx2; б) совместное распределение с.величины h1=x1+x2, h2=x1x2; в) одномерное распределение Рhi,
i=1,2.
63. Совместное распределение с.величины x1,x2 дается
числами р11=1/8, р12=1/12, р13=7/24, р21=5/24,
р22=1/6, р23=1/8, где Рij=Р{x1=xi,x2=yi}, i=1,2; j=1,3, x1=-1,x2=-1; y1=-1, y2=0, y3=1. Найти
а) одномерное распределение Рx1, Рx2; б) совместное распределение с.величины h1=x1+x2, h2=x1x2; в) одномерное распределение Рhi,
i=1,2.
64. Плотность совместного распределения величин x и h определяется равенствами f(u,v)= 1, если (u,v) Î G={(u,v): 0≤u≤2, 0≤v<1- u/2}, и f(u,v)= 0,если (u,v) ÏG. Найти fx (x).
65. Плотность совместного распределения с.величин x1иx2 fx1x2(u,v)= C(u+v), если (u,v)Î [0,1] ´ [0,1] и fx1x2(u,v)= 0,если (u,v) Î [0,1] ´ [0,1]. Найти а)постоянную С; б) fxi(xi), i=1,2; в) плотность распределения h=max(x1,x2)
66. Плотность fx1x2(u,v)= 2/p(u2+v2)3, если u2+v2³1, и 0, если u2+v2<1. Найти fh(y), если h=√x12+x22
67. Неотрицательные с.величины x1 и x2 независимы и имеют одну и ту же плотность распределения f(x), x≥0. Найти fh1h2(u,v), если h1= x1-x2 и h=√x12+x22.
68. С.величины x1 и x2 независимы и имеют одно и то же показательное распределение. Найти Р{|x1-x2|≤1}.
69. С.величины x и h независимы и имеют равномерное распределение на [0,1]. Найти плотность распределения с.величины а) x+h; б)x-h; в) xh; г) x/h.
70. С.величины x и h независимы и имеют показательное распределение с параметром l=1. Найти плотность распределения с.величин а) x+h; б)x-h; в) |x-h|; г) x/h.
71. Найти Рx+h(х), если а) x имеет равномерное распределение на [0,1], h-равномерно распределена на[0,2]; б) x имеет равномерное распределение на [0,1], h-показательное с параметром l=1; в) обе с.величины распределены по показательному закону с одним и тем же параметром; г) обе с.величины распределены по закону Пуассона с параметрами l1 и l2.
72. Найти плотность распределения с.величины h= x1/ (x1+ x2),если xi, i=1,2, независимы и равномерно распределены на [0,1].
73.
С.величины x1 и x2
независимы, P{ x1=0}=P{x1=1}=![]() , x2
равномерно распределена на отрезке [0,1]. Найти закон распределения с.величины
x1+x2.
, x2
равномерно распределена на отрезке [0,1]. Найти закон распределения с.величины
x1+x2.
74. Распределение двумерной случайной величины x определяется формулами P{x=i}=1/5,
i=0; ![]() 1,
1,![]() 2. Найти м.о. с.величины h= -x, h=|x|.
2. Найти м.о. с.величины h= -x, h=|x|.
75.
Известна fx(x)= 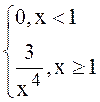 .
Найти м.о. и дисперсию с.величины x и h=1/x.
.
Найти м.о. и дисперсию с.величины x и h=1/x.
76. Найти м.о. и дисперсию с.величины, если а) P{x=m}=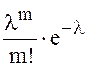 , m=0,1,2,…,
б)P{x=m}= Cnmpmqn-m , q=1-p, m=
, m=0,1,2,…,
б)P{x=m}= Cnmpmqn-m , q=1-p, m=![]() .
.
77.
fx1,x2(u,v)=![]() .
Найти Мxk,
Dxk, k=1,2,
cov(x1,x2).
.
Найти Мxk,
Dxk, k=1,2,
cov(x1,x2).
78. C. величина x равномерно распределена на [0,2p]; h1=cosx, h2=sinx. Найти Mh1, Mh2, cov(h1,h2). Являются ли h1,h2 независимыми?
79.
fx1,x2(u,v)= 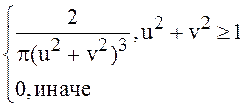
![]() . Найти М
. Найти М![]() .
.
80. C.величина имеет показательное распределение P{x>x }=e-x, x³0. Найти Мx(1-e-ax).
81.
C.величина x имеет равномерное
распределение на отрезке [0,1]. Найти cov(h1,h2), если
а) h1=аx, h2=bx, (a,b>0); б) h1=аx, h2=bx, (a<0<b);
в) h1=x, h2=x2, г)
h1=x-1/2, h2=(x-1/2)2; д) h1=sin(![]() x) , h2=cos(
x) , h2=cos(![]() x)
x)
82. Пусть (x,h) - координаты с.точки, имеющей равномерное распределение в области DÎR2. Найти r(x,h), если а) D - часть единичного круга x2+y2£1, x³0, y³0; б) D - треугольник x+y£1, x³0,y³0.
83. С. величина x и h некоррелированы. Доказать, что Mxh=MxMh.
84.
Найти ковариационную матрицу с. вектора x=(x1,x2,x3), если а)
x1,x2,x3 независимы и имеют стандартное нормальное
распределение; б)вектор x имеет равномерное
распределение в кубе{(x1,x2,x3): max |xk|£![]() }; в)
вектор x с вероятностью 1/6 принимает каждое из 6 значений
(0,0,
}; в)
вектор x с вероятностью 1/6 принимает каждое из 6 значений
(0,0,![]() ), (0,
), (0, ![]() , 0), (
, 0), (![]() ,0,0).
,0,0).
85.
Какие из матриц могут быть ковариационными для вектора x=(x1,x2,x3): а)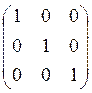 ; б)
; б)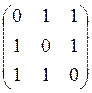 ; в)
; в) ; г)
; г)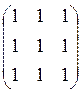 ; д)
; д)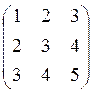 ; е)
; е)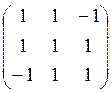 ; ж)
; ж)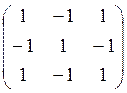 ?
?
86.
При каких х существует с.вектор x=(x1,x2,x3) с ковариационной матрицей а)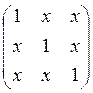 ;б)
;б)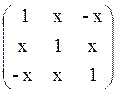 ?
?
87. Из 30 чисел 1,2,…,30 по схеме равновероятного выбора без возвращения отбирается 10 чисел. Найти м.о. суммы выбранных чисел.
88.
Неотрицательной с.величина x имеет функцию распределения F(x)=P{x<x}.Доказать, что Мx=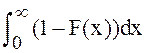
89.
C.величина x имеет функцию
распределения F(x). Доказать, что если M|x|<![]() , то
Мx=
, то
Мx=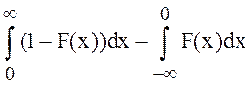 .
.
90. C.величины x ,h обладают конечными дисперсиями: Dx=s12, Dh=s22. Указать пределы, в которых может изменяться D(x+h).
91.
Найти P{|x-Mx|<3![]() x}, если x имеет : а)нормальное
распределение;
x}, если x имеет : а)нормальное
распределение;
б)показательное распределение; в)равномерное на [-1,1]; г) распределение Пуассона с Мx=0.09.
92. Координата x с.точки А на действительной прямой имеет непрерывную функцию распределения. Найти на прямой такую т. В, для которой м.о. длины отрезка АВ минимально.
93. С.величины x и h независимы и P{x=k}=P{h=k}=pqk-1, q=1-p, k=1,2,… Найти а)P{x=h}; б)P{x>h}; в)P{x<h}; г)P{x=k|x>h}; д)P{x=k|x<h}; е)P{x=k|x=h}; ж)P{x=k|x+h=l}; з)M{x|x+h=l}, l=2.
94. С. величины x и h независимы и одинаково распределены. Найти fx|x+h=z(x) в следующих случаях: а) x и h имеют показательное распределение с параметром l;
б) x и h равномерно распределены на [0,1]; в) x и h имеют распределение с f(x)=l2xe-lx,x³0.
95. Найти в условиях задачи 94 диспресию D(x|x+h=z).
96. С.величины независимы и одинаково распределены. Найти M(x|x+h=z).
97.
fxh(u,v)=![]() . Найти
fh(z|x
. Найти
fh(z|x
98. С.величины x1,x2,…,xn независимы и распределены по закону Пауссона с параметрами l1,l2,…,ln. Найти а)P{x1+…+xk=m|x1+…+xn=n}; б)M(x1+…+xm|{x1+…+xn=n).
99.
С.величины h1,h2,h3 независимы и распределены нормально с одинаковыми
параметрами а=0, r=1; h=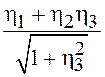 . Найти распределение h.
. Найти распределение h.
100. С.величина x имеет нормальное распределение с m=0 и σ=1.Какое из двух событий {|x|<0,7} и {|x|³0,7} имеет большую вероятность?
101. С. величина имеет стандартное нормальное распределение. Что больше: P{-0,5£x£-0,1} или P{1£x£2}?
102. С.величина x распределена нормально с параметрами (a,σ2) . Найти:
а)плотность распределения с.в. h=x2 при а=0;
б) плотность распределения с.в.h=ex при произвольных a и σ.
103.C.величины x1 и x2 независимы и имеют нормальное распределение с параметрами (a, σ 2). Найти fh(x), если h=x12+x22.
104.
С.величины xi,
i=![]() ,
имеют стандартное нормальное распределение
,
имеют стандартное нормальное распределение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.