Лабораторная работа № 2. Решение уравнения Пуассона в трехмерной области методом Зейделя

Министерство Образования Российской Федерации

Новосибирский Государственный Технический Университет

ЛАБОРАТОРНАЯ РАБОТА №2

По курсу ”Параллельное программирование ”

Тема: «Решение уравнения Пуассона в трехмерной области методом Зейделя»

Факультет          ПМИ

Группа                 ПМ-94

Студенты            Баранникова Н.Ю.

                              Кодочигова С.В.

Преподаватель  Медведев Ю.Г.

Новосибирск 2003г.

1. Условие задачи

Определить потенциал в каждой точке заданной трехмерной области при известном объемном распределении заряда в этой области, решив уравнение Пуассона в трехмерной области методом Зейделя. Реализовать параллельную программу для нескольких процессоров.

2. Постановка задачи

Трехмерная область имеет вид параллелепипеда с вершиной в точке О(0,0,0), задаются верхние границы для значений координат: Xm, Ym, Zm и число разбиений по каждой координате Ix, Iy, Iz.

Уравнение Пуассона имеет вид:

,

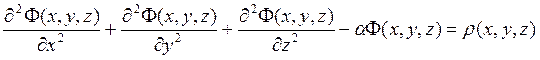краевые условия: , где - граница области .

r(x,y,z) - плотность заряда, заданная в каждой точке;

a - константа, a>0.

Разбиваем область на элементарные объемы, получаем сетку.

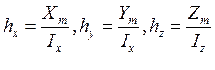Шаги сетки:

Введем обозначения:

, где i=0..Ix, j=0..Iy, k=0..Iz

Будем использовать разностную схему вида:

,    

.

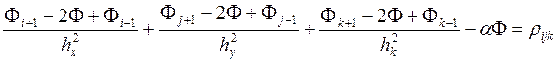Метод Зейделя для уравнения Пуассона задает итерационный процесс, в котором элементы следующей итерации вычисляются по формуле:

.

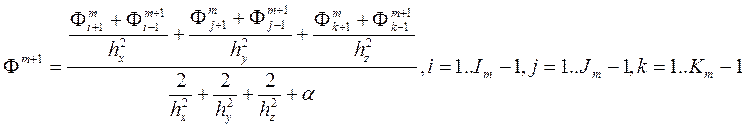Итерационный процесс останавливается, когда .

3. Ход работы

Трехмерные массивы данных распределяются между процессорами, т.е. разрезаются на блоки. Разбиение проходит по координате x. Двумерный массив данных для фиксированного значения x назовем слоем. Каждый процессор получает свою часть данных, в процессе вычислений  по необходимости обменивается крайними слоями, получает очередной результат и проверяет условие выхода. Вычисления заканчиваются, если на всех процессорах выполняется условие выхода.

Алгоритм работы:

1.  Последний процессор читает данные и раздает остальным.

2.  Если процесс не первый, он получает последний  слой предыдущего процессора (с предыдущей итерации).

3.  Если процессор не последний, он ожидает получить первый слой следующего процессора.

4.  Процессор получает новые значения для своих слоев, кроме последнего слоя. Первый процессор не вычисляет свой первый слой.

5.  Если процессор не последний, он получает значения для последнего слоя и отправляет последний слой следующему процессору.

6.  Проверяется условие выхода, если оно не выполняется хотя бы для одного процессора, возврат на шаг 2.

4. Результаты работы программы

Тестирование проводилось на rm600.sscc.ru.

Размерности данных: Ix=100, Iy=30, Iz=20. Точность 1e-5.

Число итераций: 41

5. Выводы

Судя по результатам работы программы, ускорение по времени наблюдается лишь при небольшом количестве процессоров. При дальнейшем росте числа процессоров результат по времени ухудшается, возможно, из-за увеличения числа пересылок данных, так как затраты по времени на отправление и прием данных больше, чем затраты на вычисления.

6.Текст программы

#include<mpi.h>

#include<stdio.h>

#include<stdlib.h>

#include<sys/time.h>

int dim,ost,rank,size,tag=1;

float **r,**F;// м-цы потенциалов и ро

int Ix,Iy,Iz,  // размерности данных

M,dt1;

float hx2,hy2,hz2,eps,c;

float Abs(float a)

{return(a>0 ? a : (-1*a));

}

void xdims(int * dims,int * disps) // заполнение массивов размерностей и 

//смещений

{int i,j;

for(i=0;i<ost;i++) {dims[i]=dim+1;disps[i]=0;}

for(i=ost;i<size;i++) {dims[i]=dim;disps[i]=0;}

for(i=size-1;i>=0;i--)

for(j=0;j<i;j++) disps[i]+=dims[j];

}

int vichisl(int l) // Вычисление l-го слоя

{int i,j,flag; // flag=1-точность достигнута

float fold,fl,fi,fj;

for(i=1;i<Iy-1;i++)//0-я и последняя границы заданы краевыми усл-ми

for(j=1;j<Iz-1;j++)

{fold=F[l][i*Iz+j];

fl=(F[l+1][i*Iz+j]+F[l-1][i*Iz+j])/hx2;

fi=(F[l][(i+1)*Iz+j]+F[l][(i-1)*Iz+j])/hy2;

fj=(F[l][i*Iz+j+1]+F[l][i*Iz+j-1])/hz2;

F[l][i*Iz+j]=(fl+fi+fj-r[l-1][i*Iz+j])/c;