Решение уравнения Пуассона в трехмерной области методом Зейделя

МО РФ

НГТУ

кафедра ПВС

Лабораторная работа

по дисциплине «основы параллельного программирования»

РЕШЕНИЕ УРАВНЕНИЯ ПУАССОНА В ТРЕХМЕРНОЙ ОБЛАСТИ МЕТОДОМ ЗЕЙДЕЛЯ

факультет      ПМИ

группа            ПМ-93

выполнили     Катарушкина ТС

Киселева МВ

Ли ММ

принял           Медведев ЮГ

Новосибирск 2003

Условие задачи

Решить уравнение Пуассона в трехмерной области методом Зейделя.

Текст программ

#define ijk(i,j,k) (i)*m[1]*m[2]+(j)*m[2]+(k)

#define x(i) xyz[0][0]+(i)*h[0]

#define y(j) xyz[1][0]+(j)*h[1]

#define z(k) xyz[2][0]+(k)*h[2]

#define max(a,b) (((a) > (b)) ? (a) : (b))

#define dabs(a) (((a) > 0 ) ? (a) : -(a))

#include "mpi.h"

#include <stdio.h>

#include <stdlib.h>

#include <time.h>

double F(double x,double y,double z)

{

return(x+y+z);

}

double P(double x,double y,double z,double alpha)

{

return(-alpha*(x+y+z));

}

int main(int argc, char *argv[])

{

FILE *f;

time_t t_s,t_e;

int rank , size;                    //Ёрэъ ш ўшёыю ъюья-ют

int i,j,k,l,d,ii,exit_flag;

double *fi,*ro,fi_ijk;

int    *flags;

double alpha,eps,eps_current;

double xyz[3][2];                   //{{x0,x1},{y0,y1},{z0,z1}}

int    m[3];                        //{mx,my,mz}ЁрчьхЁэюёЄ№

double h[3];                        //{hx,hy,hz}

MPI_Status st;

MPI_Init(&argc,&argv);

MPI_Comm_size(MPI_COMM_WORLD,&size);

MPI_Comm_rank(MPI_COMM_WORLD,&rank);

if (rank == size-1)

{

f=fopen("info.dat","r+");

fscanf(f,"%lf %lf %d",&xyz[0][0],&xyz[0][1],&m[0]);

fscanf(f,"%lf %lf %d",&xyz[1][0],&xyz[1][1],&m[1]);

fscanf(f,"%lf %lf %d",&xyz[2][0],&xyz[2][1],&m[2]);

fscanf(f,"%lf",&alpha);

fscanf(f,"%lf",&eps);

fclose(f);

h[0]=(xyz[0][1]-xyz[0][0])/(m[0]-1);

h[1]=(xyz[1][1]-xyz[1][0])/(m[1]-1);

h[2]=(xyz[2][1]-xyz[2][0])/(m[2]-1);

}

MPI_Bcast(&m,3,MPI_INT,size-1,MPI_COMM_WORLD);

MPI_Bcast(&xyz,2*3,MPI_DOUBLE,size-1,MPI_COMM_WORLD);

MPI_Bcast(&h,3,MPI_DOUBLE,size-1,MPI_COMM_WORLD);

MPI_Bcast(&alpha,1,MPI_DOUBLE,size-1,MPI_COMM_WORLD);

MPI_Bcast(&eps,1,MPI_DOUBLE,size-1,MPI_COMM_WORLD);

l=(rank<m[0]%size)?m[0]/size+1+(1+1):m[0]/size+(1+1);

if(rank==size-1) l=(rank<m[0]%size)?m[0]/size+1+(1+0):m[0]/size+(1+0);

if(rank==0) l=(rank<m[0]%size)?m[0]/size+1+(0+1):m[0]/size+(0+1);

fi    =(double*)malloc(l*m[1]*m[2]*sizeof(double));

ro    =(double*)malloc(l*m[1]*m[2]*sizeof(double));

flags =(int*)malloc(size*sizeof(int));

for (i=0;i<size;i++) flags[i]=0;

d=(rank<m[0]%size)?rank*(m[0]/size+1):m[0]%size+rank*(m[0]/size);

printf("Rank = %d D = %d L=%d\n",rank,d,l);

for(i=0;i<l;i++)

for(j=0;j<m[1];j++)

for(k=0;k<m[2];k++)

{

fi[ijk(i,j,k)]=F(x(i+d+((rank==0)?0:-1)),y(j),z(k));

ro[ijk(i,j,k)]=P(x(i+d+((rank==0)?0:-1)),y(j),z(k),alpha);

}

for(i=0;i<l;i++)

for(j=1;j<m[1]-1;j++)

for(k=1;k<m[2]-1;k++)

{

fi[ijk(i,j,k)]=0.e0;

}

if (rank == 0)

{

for(j=0;j<m[1];j++)

for(k=0;k<m[2];k++)

{

fi[ijk(0,j,k)]=F(x(0+d),y(j),z(k));

}

}

if (rank == size-1)

{

for(j=0;j<m[1];j++)

for(k=0;k<m[2];k++)

{

fi[ijk(l-1,j,k)]=F(x((l-1)+d-1),y(j),z(k));

}

}

if(rank == 0) time(&t_s);

/*---------------------------------------------*/

do

{     

if (rank != 0)

{

MPI_Send(&fi[ijk(1,0,0)],m[1]*m[2],MPI_DOUBLE,rank-1,15,MPI_COMM_WORLD);

MPI_Recv(&fi[ijk(0,0,0)],m[1]*m[2],MPI_DOUBLE,rank-1,16,MPI_COMM_WORLD,&st);

}

eps_current=0.e0;

for(i=1;i<l-1;i++)

for(j=1;j<m[1]-1;j++)

for(k=1;k<m[2]-1;k++)

{

fi_ijk=1.e0/(alpha+2/(h[0]*h[0])+2/(h[1]*h[1])+2/(h[2]*h[2]))*

((fi[ijk(i+1,j,k)]+fi[ijk(i-1,j,k)])/(h[0]*h[0])+

(fi[ijk(i,j+1,k)]+fi[ijk(i,j-1,k)])/(h[1]*h[1])+

(fi[ijk(i,j,k+1)]+fi[ijk(i,j,k-1)])/(h[2]*h[2])ro[ijk(i,j,k)]);

eps_current=max(eps_current,dabs((fi[ijk(i,j,k)]-fi_ijk)/fi_ijk));

fi[ijk(i,j,k)]=fi_ijk;

}

//      printf("Rank = %d eps_current = %1.12lf\n",rank,eps_current);

if (rank != size-1)

{

MPI_Recv(&fi[ijk(l-1,0,0)],m[1]*m[2],MPI_DOUBLE,rank+1,15,MPI_COMM_WORLD,&st);

MPI_Send(&fi[ijk(l-2,0,0)],m[1]*m[2],MPI_DOUBLE,rank+1,16,MPI_COMM_WORLD);

}

flags[rank]=(eps>eps_current);

MPI_Allgather(&flags[rank],1,MPI_INT,flags,1,MPI_INT,MPI_COMM_WORLD);

exit_flag=1;

for(i=0;i<size;i++) exit_flag*=flags[i];

}

while (!exit_flag);

/*---------------------------------------------*/

if(rank == 0)

{

f=fopen("result.dat","w+");

time(&t_e);

fprintf(f,"Number of Process = %d Time = %d sec\n",size,t_e-t_s);

for(i=0;i<l-1;i++)

for(j=0;j<m[1];j++)

for(k=0;k<m[2];k++)

fprintf(f,"F(%lf,%lf,%lf) = %lf(%lf) \n",x(i+d),y(j),z(k),fi[ijk(i,j,k)],F(x(i+d),y(j),z(k)));

for(ii=1;ii<size;ii++)

{

d=(ii<m[0]%size)?ii*(m[0]/size+1):m[0]%size+ii*(m[0]/size);

l=(ii<m[0]%size)?m[0]/size+1+(1+1):m[0]/size+(1+1);

if(ii==size-1) l=(ii<m[0]%size)?m[0]/size+1+(1+0):m[0]/size+(1+0);

if(ii==0) l=(ii<m[0]%size)?m[0]/size+1+(0+1):m[0]/size+(0+1);

MPI_Recv(fi,l*m[1]*m[2],MPI_DOUBLE,ii,17,MPI_COMM_WORLD,&st);

if(ii!=size-1) l=l-1;

for(i=1;i<l;i++)

for(j=0;j<m[1];j++)

for(k=0;k<m[2];k++)

fprintf(f,"F(%lf,%lf,%lf) = %lf(%lf) \n",x(i+d-1),y(j),z(k),fi[ijk(i,j,k)],F(x(i+d-1),y(j),z(k)));

}

fclose(f);

}

else

{

MPI_Send(fi,l*m[1]*m[2],MPI_DOUBLE,0,17,MPI_COMM_WORLD);

}

free(ro);

free(flags);

free(fi);

MPI_Finalize();

return(0);

}

Тесты и выводы

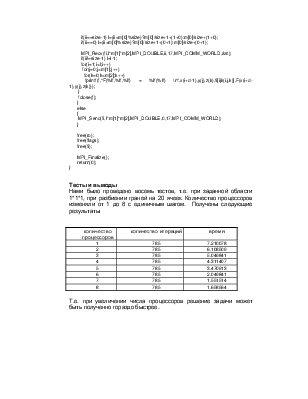
Нами было проведено восемь тестов, т.е. при заданной области       1*1*1, при разбиении граней на 20 ячеек. Количество процессоров изменяли от 1 до 8 с единичным шагом.  Получены следующие результаты

количество процессоров	количество итераций	время
1	785	7.210078
2	785	6.108509
3	785	5.049841
4	785	4.311407
5	785	3.470913
6	785	2.049841
7	785	1.551514
8	785	1.658564

Т.е. при увеличении числа процессоров решение задачи может быть полученно гораздо быстрее.