пространства ![]() достаточно выписать условие
ортогональности невязки всем базисным векторам этого подпространства:
достаточно выписать условие
ортогональности невязки всем базисным векторам этого подпространства: ![]() ,
, ![]() , при этом не требуется самосопряжённость оператора
, при этом не требуется самосопряжённость оператора ![]() .
.
Важным в построении дискретного аналога является выбор пространства и системы базисных функций.
Умножим исходное уравнение в пространстве ![]() на базисные функции - пробные функции
на базисные функции - пробные функции ![]() , где
, где ![]() из
пространства, где базисные функции удовлетворяют однородным краевым
условиям.
из
пространства, где базисные функции удовлетворяют однородным краевым
условиям.
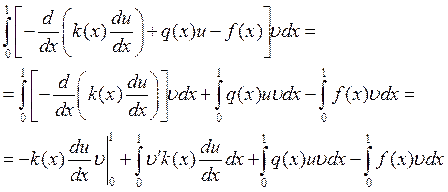
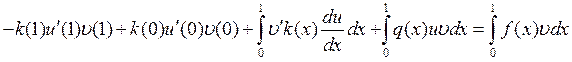
![]() ,
, ![]() , так
как либо поток
, так
как либо поток ![]() , либо выберем такие
, либо выберем такие ![]() .
.
Поскольку приближённое решение ![]() принадлежит
подпространству
принадлежит
подпространству ![]() , то может быть представлено в
виде линейной комбинации базисных финитных функций:
, то может быть представлено в
виде линейной комбинации базисных финитных функций:
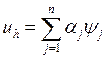 , где
, где ![]() - базисные функции пространства, для
которых пробные являются подпространством.
- базисные функции пространства, для
которых пробные являются подпространством.
В общем случае любая пробная функция может быть представлена в виде линейной комбинации
![]() , но когда
будем выписывать уравнения для каждого
, но когда
будем выписывать уравнения для каждого ![]() , то
будет иметь место представление
, то
будет иметь место представление ![]() ,
, ![]() .
.
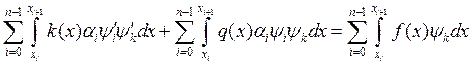 ,
, ![]() .
.
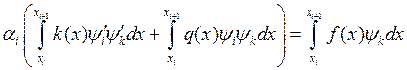 ,
, ![]() .
.
Таким образом, мы получили матрицу СЛАУ, решив которую получим веса функции в узлах.
Поскольку в качестве базисных функций выбраны финитные функции вида:
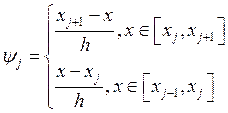 , которые не равны нулю на конечном интервале, таким образом,
перейдем к этому конечному промежутку – конечному элементу и рассмотрим на нём
локальные матрицы массы, жёсткости и вектора правой части.
, которые не равны нулю на конечном интервале, таким образом,
перейдем к этому конечному промежутку – конечному элементу и рассмотрим на нём
локальные матрицы массы, жёсткости и вектора правой части.
Введём обозначения:
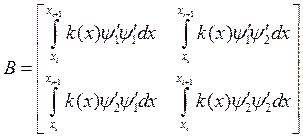 матрица массы
матрица массы
С условием интерполяции функции ![]() ,
матрица массы примет вид:
,
матрица массы примет вид:
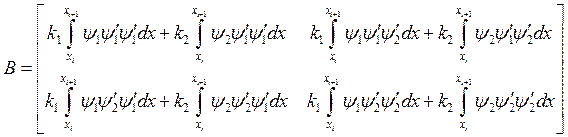
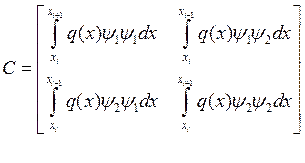 матрица жёсткости или с учётом интерполяции функции
матрица жёсткости или с учётом интерполяции функции ![]() :
:
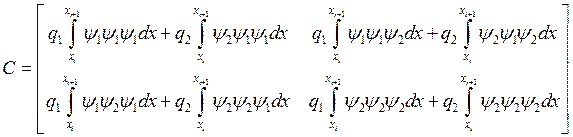
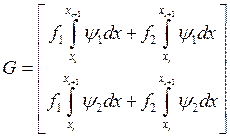 вектор
правой части
вектор
правой части
Посчитав эти интегралы, получаем следующие локальные матрицы массы и жёсткости, а также локальный вектор правой части:
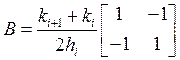 ,
,
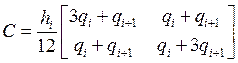 ,
,
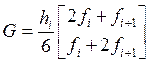 .
.
Локальная матрица ![]() .
.
Замечание.
Как видно интерполяция функции ![]() совпадает
с усреднённым значением функции на отрезке.
совпадает
с усреднённым значением функции на отрезке.
2.2. Алгоритм сборки глобальной матрицы СЛАУ и глобального вектора правой части. Метод решения СЛАУ.
Для непрерывности базисных функций в каждом узле ![]() , где базисные функции с различных конечных
элементов принимают значение равное единице, производим их «склейку». Поэтому
глобальная матрица получается из локальных матриц путем некоторого вклада –
наложения частей одной локальной матрицы на часть другой локальной матрицы:
, где базисные функции с различных конечных
элементов принимают значение равное единице, производим их «склейку». Поэтому
глобальная матрица получается из локальных матриц путем некоторого вклада –
наложения частей одной локальной матрицы на часть другой локальной матрицы: ![]() . Вид глобальной матрицы приведён в
приложении 1.1. Вид глобального вектора приводить не будем по той причине, что
он очевиден:
. Вид глобальной матрицы приведён в
приложении 1.1. Вид глобального вектора приводить не будем по той причине, что
он очевиден: ![]() .
.
После ассемблирования глобальной матрицы и глобального
вектора получили трехдиагональную матрицу. Решим полученную СЛАУ ![]() методом
методом ![]() разложения.
разложения.
2.3. Описание алгоритма решения краевой задачи
Поскольку задача линейная, т.е. ![]() , то
особых трудностей для решения задачи не возникает.
, то
особых трудностей для решения задачи не возникает.
1. Построить
глобальную матрицу ![]()
2. Сформировать
вектор правой части ![]()
3. Учесть краевые условия:
- первые и третьи краевые условия учитываются следующим образом:
для первого ![]() – в вектор правой части ставим
– в вектор правой части ставим ![]() , а в матрице на место элемента
, а в матрице на место элемента ![]() записываем единицу и все элементы этой
строки зануляем, поскольку первое краевое условие явно определяет вес в узле.
Далее проводим симметризацию матрицы;
записываем единицу и все элементы этой
строки зануляем, поскольку первое краевое условие явно определяет вес в узле.
Далее проводим симметризацию матрицы;
для третьего 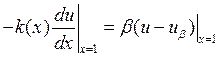 элемент матрицы
элемент матрицы ![]() ,
а в векторе правой части
,
а в векторе правой части ![]() .
.
- вторые и первые краевые условия:
для учёта второго 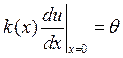 добавка
добавка ![]() идёт
только в вектор правой части;
идёт
только в вектор правой части;
учет первого аналогичен описанному выше.
4. Решить СЛАУ ![]()
2.4. Анализ результатов вычислительных экспериментов
Линейная функция
1.1.
Таблица №1 и №2
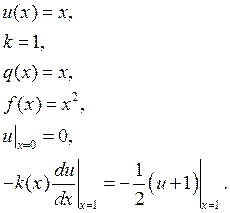
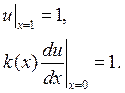
Результаты, когда значение ![]() бралось,
как усредненное значение оказываются на порядок хуже, чем когда функция
бралось,
как усредненное значение оказываются на порядок хуже, чем когда функция ![]() была интерполирована.
была интерполирована.
При исследовании получения решения на вложенных сетках «лучшее» решение получаем при увеличении числа узлов сетки, иными словами, при уменьшении шага в два раза погрешность уменьшается как минимум в два раза.
При ![]() не получаем точного решения,
хотя казалось бы функция
не получаем точного решения,
хотя казалось бы функция ![]() - линейная
- линейная
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.