Решение задачи Пуассона

Министерство образования Российской Федерации

НГТУ

Кафедра параллельных вычислительных технологий

Лабораторная работа по курсу «Основы параллельного программирования»

Тема: «Решение задачи Пуассона»

Факультет:       ПМИ

Группа:          ПМ-91

Студенты:        Купреев А. В., Крыцын Ю. С.

Преподаватель:   Медведев Ю. Г.

Новосибирск 2003

I.  Цели работы

Реализовать программу решения задачи Пуассона на прямоугольной сетке в MPI.

Реализация

Используется следующая схема распараллеливания вычислений (на каждой итерации):

·  Если процесс не нулевой, то он должен отправить свой первый слой левому соседу и ждать, пока тот не пришлет ему свой последний слой.

·  Пересчитать все свои слои, кроме первого и последнего.

·  Если процесс не последний, то: получить первый слой правого соседа, пересчитать свой последний слой и отправить его правому соседу.

Выход из программы будет осуществляться по ограничению на число итераций или по норме шага приближения. Для минимизации вызовов функций пересылки данных воспользуемся тем, что процессы на каждой итерации по цепочке обмениваются своими граничными слоями как в прямом направлении, так и в обратном. После полного просчета очередной итерации, процесс должен отправлять норму своего шага следующему процессу вместе со своим последним слоем. Таким образом, к последнему процессу приходит норма полного шага. Последний процесс должен проверить условие выхода по точности, и если точность достигнута, то к обратной волне слоев добавить флаг выхода. Используя эту схему мы уменьшим количество пересылок до минимально возможного. Так как в языке Си содержимое многомерного массива разрывно в памяти, то трехмерную сетку будем представлять одномерным массивом, а для удобства определим функцию, которая будет переводить трехмерные координаты в одномерные. Для быстроты обращения к элементам массива эту функцию необходимо сделать встраиваемой (inline).

II. Постановка задачи

Трехмерная область имеет вид параллелепипеда с вершиной в точке О(0,0,0), задаются верхние границы для значений координат: Xm, Ym, Zm и число разбиений по каждой координате Ix, Iy, Iz.

Уравнение Пуассона имеет вид:

,

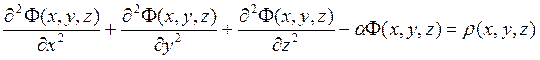краевые условия: , где - граница области .

(x,y,z) плотность заряда, заданная в каждой точке;

a - константа, a>0.

Разбиваем область на элементарные объемы, получаем сетку.

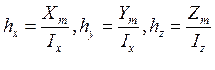Шаги сетки:

Введем обозначения:

, где i=0..Ix, j=0..Iy, k=0..Iz

Будем использовать разностную схему вида:

,    

.

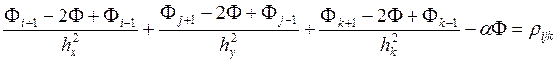Метод Зейделя для уравнения Пуассона задает итерационный процесс, в котором элементы следующей итерации вычисляются по формуле:

.

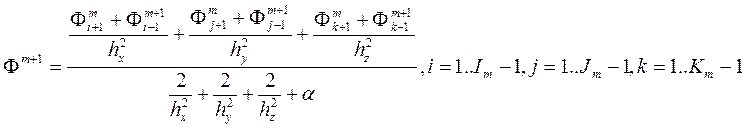Итерационный процесс останавливается, когда .

III. Результаты тестирования:

В качестве тестовой функции использовалась функция u(x,y,z)=x^3+y^3+z^3; Начальное приближение – единичная во всех узлах функция, требуемая норма шага итерации – 0.01

Программа тестировалась на серверах fpm и rm600.

При тестировании использовалась сетка в 1000, 4, 4 точек по координатам x,y и z соответственно на параллелепипед [(0,0,0), (5,2,2)].

На сервере fpm получили следующие результаты: при использовании 3 процессов время счета составило 187 с.

На сервере rm600 получили следующие результаты: при использовании 3 процессоров:   154 с.

при использовании 4 процессоров:   137 с.

при использовании 5 процессоров:   1028 с.

при использовании 6 процессоров:   1373 с.

При виде таких странных результатов были проведены дополнительные исследования: Программа запускалась несколько раз подряд на одном числе процессоров с одними исходными данными и время счета при этом изменялось от 142 с до 1020 с. Кроме того, замечено, что время работы других программ так же сильно зависит от числа используемых процессоров.

Делаем вывод: сервер rm600 находится в состоянии неприемлемом для тестирования программного обеспечения!
 

IV. Приложение (текст программы)

#include <mpi.h>

#include <stdio.h>

#include <time.h>

const int TheTag=1;

const int TheSizeTag=2;

const int TheEpsTag=3;

const int TheFinTag=4;

int MaxX, MaxY, MaxZ;

int LoadFirst(float *Phi, float *F, int BlockSize, int cntY, int cntZ, int Rank, float Hx, float Hy, float Hz);

main(int argc, char ** argv)

{

MPI_Status st;

MPI_Request rec1,rec2,rec3;

int PrCount, MatrSize, Rank, BlockSize, k, i, j, m, h, BlockNo, FullBlocks;

int MaxI,MaxJ, Flag, flag1,flag2,Iter;

float *Phi, A, *F, Eps, CurEps, PrevEps,*Layer1, *Layer2;

float Hx, Hy, Hz, temp, temp2;

int cntX, cntY, cntZ;

float tempPhi;

time_t start;

FILE *IniFile, *ResFile;

MPI_Init(&argc,&argv);

MPI_Comm_rank(MPI_COMM_WORLD,&Rank);

MPI_Comm_size(MPI_COMM_WORLD,&PrCount);

Flag=0;

my_init(&Hx, &Hy, &Hz, &cntX, &cntY, &cntZ);

MaxY=cntY; MaxZ=cntZ;

/* // BlockSize calculation ======================================== */

if (cntX % PrCount==0) {

BlockSize=cntX/PrCount;

FullBlocks=PrCount;

}

else

{

BlockSize=cntX/PrCount+1;

FullBlocks=cntX % PrCount;

}                                     

Phi = (float *) malloc((BlockSize*cntY*cntZ+1)*sizeof(float));

F = (float *) malloc(BlockSize*cntY*cntZ*sizeof(float));

Layer1 = (float *) malloc((cntY*cntZ+1)*sizeof(float));

if ((Phi==NULL)||(F==NULL))

{

printf("process %i: invalid malloc\n",Rank);

MPI_Finalize();

}