Рекурсивный алгоритм распознавания образов

МО РФ

Новосибирский  государственный технический  университет

Кафедра ПМт

Курсовой проект

по предмету

"Методы планирования и анализа"

на тему:

«Рекурсивный алгоритм распознавания образов»

Факультет: ПМИ

Группа: ПМ-81

Студенты:   Д.С. Моисеев

Преподаватель:  И.А. Полетаева

г. Новосибирск 2002г.

1. Аннотация

Данная работа посвящена решению задач распознавания образов на основе использования рекурсивного отображения многомерного пространства на числовую ось.

Разграничение образов осуществляется по средствам решающих функций.

Само разграничение между классами осуществляется посредством выборочной решающей функции, построенной на основе вида решающей функции и обучающей выборке.

Т.е. на основе информации об обучающей выборке необходимо построить решающее правило, которое по значениям p признаков определяет номер класса для любого объекта, не входящего в обучающую выборку.

2. Теоретические основы метода

На основе информации об обучающей выборке необходимо построить решающее правило, которое по значениям p признаков определяет номер класса для любого объекта, не входящего в обучающую выборку.

Определим исходные данные в дискретном пространстве размерности p с номером разбиения m. Для этого необходимо предварительно пронормировать значения каждого признака с учетом допустимых преобразований данной шкалы к интервалу [0,1).

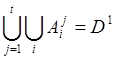Образы объектов обучающей выборки строятся с использованием рекурсивного отображения , а построение решающего правила состоит в разбиении  на системы отрезков следующим образом:,  , для

Тогда для принятия решения о принадлежности представленного объекта к классу  достаточно отобразить его в , тем самым определив систему отрезков, в который входит образ объекта.

Т.о. процесс построения решающего правила будет выглядеть следующим образом.

Пусть обучающая выборка для первого класса есть выборка из генеральной совокупности с плотностью f(x), . Оценим значение плотности в произвольной точке , используя лишь координаты образов объектов обучающей выборки в . В качестве оценки функции f(x) возьмем величину частости попадания объектов обучающей выборки в некоторую окрестность   точки : т.е.        , где

- число объектов обучающей выборки первого класса, попавших в

- длина окрестности  

n- число объектов первого класса в обучающей выборке.

Можно показать, что предложенная оценка сходится к f(x) при . Пусть в окрестность  точки , ,попадает образов объектов обучающей выборки первого класса. Окрестность  представляет собой отрезок прямой, длиной . Ей в свою очередь соответствует в область . В силу свойств отображения  справедливы следующие утверждения: - связна; ; в  попадает  объектов обучающей выборки первого класса, образцы которых попадают в ;    в связи с совпадением квантов  и .

Таким образом, 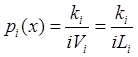, где - объем окрестности . Если построить вокруг точки  систему отрезков, стягивающихся со скоростью, меньшей чем 1/n при , то оценка  будет среднеквадратически сходиться к плотности f(x), т.к.  сходится среднеквадратически к f(x) и .

Оценки плотностей распределений для остальных распознаваемых классов получаются аналогично.

Т.о. решающее правило в определяется множеством точек , в которых выполняется условие равенства функций плотности распределения различных классов.

3. Описание программы

Для проведения исследований была разработана программа, позволяющая достаточно удобно (с точки зрения создателя) анализировать поставленную в работе задачу.

Программа является полностью настраиваемой на любое число классов, наблюдений и любой набор переменных.

Существует возможность использовать как уже созданные данные (чтение из файла), так и создавать эти данные в процессе работы с программой с последующим возможным сохранением анализируемых данных (запись в файл).

Так же в процессе работы с программой существует возможность просмотра текущего набора данных.

По результатам проводимого над данными пользователя анализа:

·  программа подсчитывает число ошибок, используя обучающую выборку в качестве экзаменующей;

·  позволяет пользователю провести распознавание заданного им (в рамках определённых им ранее параметров данных) образа.

4. Инструкция пользователю

Работа с программой начинается с определения набора данных (размерность выборки, число классов и непосредственно сама выборка). Данная операция можно осуществить двумя способами:

·  выбор данных из ранее сохранённого файла по средствам выполнения операции «Читать данные из файла»;

·  создание нового набора данных, для чего следует занести информацию о числе переменных и числе классов в соответствующие поля формы и добавлять данные по средствам операции «Добавить наблюдения вручную» (с указанием выборки и номера класса, к которому она принадлежит – число, не превышающее числа классов). Следует отметить, что как только хотя бы одно наблюдение добавлено, изменять число классов и число переменных невозможно.

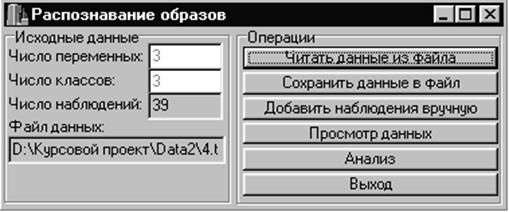
После создания данных их можно просмотреть, используя операцию «Просмотр данных».

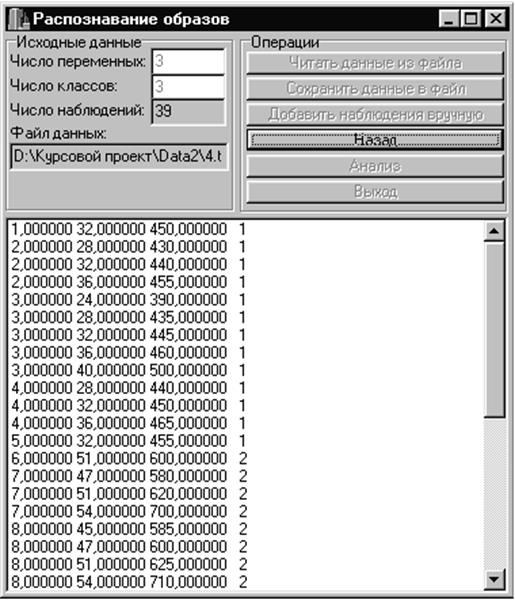
Анализ над данными проводится, после активизации операции «Анализ».

В результате анализа существует возможность:

·  посмотреть число ошибок, полученных в результате использования обучающей выборки в качестве экзаменующей, в поле «Число ошибок»;