



Мера, заданная на ![]() – функция
– функция ![]() , если выполнены следующие условия:
, если выполнены следующие условия: ![]() ; для любого счетного набора попарно
непересекающихся множеств
; для любого счетного набора попарно
непересекающихся множеств ![]() таких,
что
таких,
что 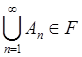 , выполнено свойство счетной
аддитивности (
, выполнено свойство счетной
аддитивности (![]() -аддитивности):
-аддитивности):
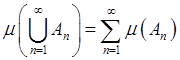 ,
, ![]() - некоторое
измеримое пространство.
- некоторое
измеримое пространство.
Мера конечна, если дополнительно выполнено условие ![]() .
.
Свойства:
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
Если ![]() - убывающая
последовательность такая, что
- убывающая
последовательность такая, что 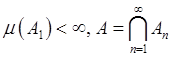 , то
, то
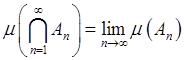 . Если последовательность
. Если последовательность ![]() - возрастающая и такая, что
- возрастающая и такая, что 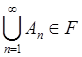 , то
, то 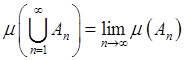 .
.
Вещественная функция ![]() называется
называется ![]() -измеримой или просто измеримой,
если
-измеримой или просто измеримой,
если ![]() и
и ![]() - борелевская
- борелевская ![]() -алгебра на
-алгебра на ![]() при условии, что
при условии, что ![]() - некоторое измеримое пространство.
- некоторое измеримое пространство.
Случайная величина – измеримая функция ![]() , ставящая в соответствие каждому
элементарному исходу
, ставящая в соответствие каждому
элементарному исходу ![]() число
число
![]() , где
, где ![]() - некоторое вероятностное
пространство.
- некоторое вероятностное
пространство.
Функция измерима, если все множества ![]() , т.е. являются событиями для любого
борелевского множества
, т.е. являются событиями для любого
борелевского множества ![]() .
.
![]()
Функция распределения (вероятностей) случайной
величины ![]() называется
функция
называется
функция ![]() , значение
которой в точке
, значение
которой в точке ![]() равно
вероятности события
равно
вероятности события ![]() , т.е.
, т.е. ![]() .
.
Свойства:
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
; ![]() ;
;
4.
![]() - непрерывная
справа функция в каждой точке
- непрерывная
справа функция в каждой точке ![]() ;
;
5.
![]() ;
;
6.
![]() ;
;
7.
![]() .
.
![]() Дискретная
случайная величина – случайная величина
Дискретная
случайная величина – случайная величина ![]() , для которой ступенчатая функция
, для которой ступенчатая функция ![]() , имеющая в точках
, имеющая в точках ![]() скачки, величина которых равна
соответственно
скачки, величина которых равна
соответственно ![]() , является
функцией распределения, или если каждому элементарному исходу ставится в
соответствие одно число из конечного или счетного множества чисел
, является
функцией распределения, или если каждому элементарному исходу ставится в
соответствие одно число из конечного или счетного множества чисел ![]() , причем вероятность события
, причем вероятность события ![]() .
.
Ряд распределения – способ задания дискретной случайной величины. Аналог плотности распределения для непрерывных случайных величин.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ограничения на ![]() :
:
1.
![]() ;
;
2.
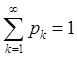 , т.к.
, т.к. ![]() .
.
Закон распределения случайной величины ![]() или просто распределение
случайной величины – это такая характеристика вместо функции распределения, по
которой возможно однозначно восстановить функцию распределения.
или просто распределение
случайной величины – это такая характеристика вместо функции распределения, по
которой возможно однозначно восстановить функцию распределения.
По ряду распределения можно восстановить функцию
распределения: ![]() , где
, где 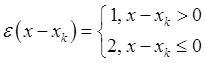 .
.
Функция распределения дискретной случайной, являющейся
константой: 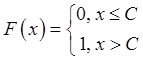 .
.
Функция распределения индикатора события ![]() :
: 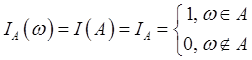 .
.
Если ![]() - дискретное
вероятностное пространство,
- дискретное
вероятностное пространство, ![]() - некоторая
случайная величина, принимающая значения
- некоторая
случайная величина, принимающая значения ![]() и
и ![]() , то
, то 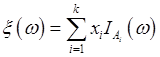 , где множества
, где множества ![]() образуют разбиение пространства
образуют разбиение пространства ![]() . Тогда ряд распределения случайной
величины
. Тогда ряд распределения случайной
величины ![]() и функция
распределения имеют следующий вид:
и функция
распределения имеют следующий вид:
|
|
|
|
|
|
|
|
|
![]() ,
, ![]() : биномиальный закон
распределения с параметрами распределения
: биномиальный закон
распределения с параметрами распределения ![]() и
и ![]() . Функция распределения имеет вид:
. Функция распределения имеет вид: 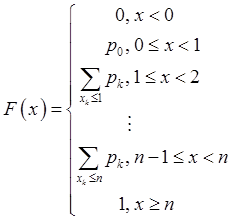 .
.
![]() ,
, ![]() : геометрический закон
распределения с параметром
: геометрический закон
распределения с параметром ![]() .
. ![]() : отсутствие последействия –
условная вероятность того, что событие будет продолжаться
: отсутствие последействия –
условная вероятность того, что событие будет продолжаться ![]() времени, если известно, что она не
закончено за
времени, если известно, что она не
закончено за ![]() времени,
совпадает с вероятностью того, что событие будет продолжаться
времени,
совпадает с вероятностью того, что событие будет продолжаться ![]() времени.
времени.
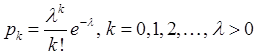 ,
, ![]() : пуассоновское распределение
с параметром
: пуассоновское распределение
с параметром ![]() используется в
теории надежности и теории массового обслуживания.
используется в
теории надежности и теории массового обслуживания.
Плотность распределения (вероятностей) случайной
величины ![]() - это такая
функция
- это такая
функция ![]() , что
, что 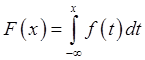 (учитывая, что интеграл сходится). Плотность
определяет закон распределения случайной величины.
(учитывая, что интеграл сходится). Плотность
определяет закон распределения случайной величины.
Непрерывная случайная величина – случайная величина,
функция распределения которой ![]() представима
в виде интеграла
представима
в виде интеграла 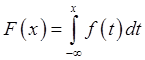 .
.
Т.к. на практике функция плотности распределения является
непрерывной почти всюду на области определения, поэтому почти всюду выполняется
равенство ![]() .
.
Свойства плотности распределения:
1.
![]() ;
;
2.
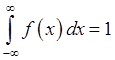 ;
;
3.
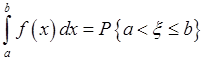 .
.
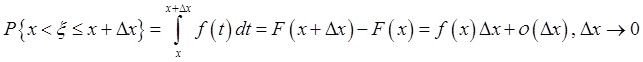
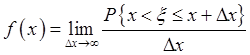
Для произвольного множества ![]() :
: ![]()
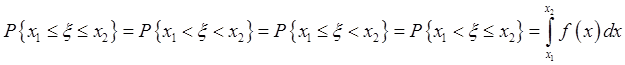 ,
, 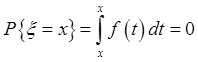
![]() : равномерно
распределенная на отрезке
: равномерно
распределенная на отрезке ![]() случайная
величина
случайная
величина ![]() имеет плотность
распределения
имеет плотность
распределения 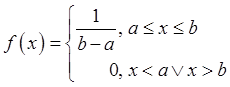 , функция
распределения
, функция
распределения 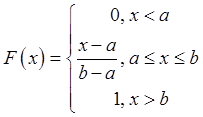 , вероятность
попадания случайной величины на интервал
, вероятность
попадания случайной величины на интервал ![]() :
: 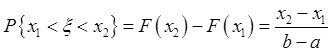 .
.
![]() : экспоненциальное
(показательное) распределение с плотностью распределения
: экспоненциальное
(показательное) распределение с плотностью распределения 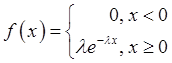 и функция распределения
и функция распределения 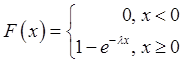 , где
, где ![]() - параметр распределения. Обладает отсутствие
последействия – если непрерывная случайная величина обладает этим свойством,
то вероятность попадания в любой интервал длины
- параметр распределения. Обладает отсутствие
последействия – если непрерывная случайная величина обладает этим свойством,
то вероятность попадания в любой интервал длины ![]() не зависит от того, где на числовой
прямой расположено начала интервала, эта вероятность зависит только от длины
интервала.
не зависит от того, где на числовой
прямой расположено начала интервала, эта вероятность зависит только от длины
интервала.
Характеристическое свойство экспоненциально распределенных случайных величин – отсутствие последействие.
![]() : нормальное
(гауссово) распределение имеет плотность распределения
: нормальное
(гауссово) распределение имеет плотность распределения 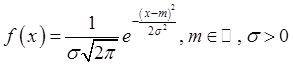 , функцию распределения
, функцию распределения 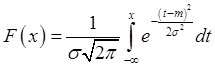 , где
, где ![]() - среднее значение случайной
величины,
- среднее значение случайной
величины, ![]() - среднее
квадратичное (квадратическое) отклонение.
- среднее
квадратичное (квадратическое) отклонение.
![]() : «правило
трех сигм» – нормальная случайная величина практически никогда не
отклоняется от своего среднего значения
: «правило
трех сигм» – нормальная случайная величина практически никогда не
отклоняется от своего среднего значения ![]() более чем на
более чем на ![]() .
.
При ![]() ,
, ![]() нормальный закон называют стандартным
нормальным законом распределения, плотность которого
нормальный закон называют стандартным
нормальным законом распределения, плотность которого 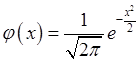 и функция распределения которого
и функция распределения которого 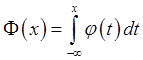 .
.
Нормальное распределение случайной величины используется в практических задачах математической статистики, случайных процессов.
Распределение Вейбулла: ![]() ,
, ![]() , подчиняет
время безотказной работы многих технических устройств. При
, подчиняет
время безотказной работы многих технических устройств. При ![]() превращается в
превращается в ![]() , при
, при ![]() - распределение Рэлея.
- распределение Рэлея.
Гамма-распределение: 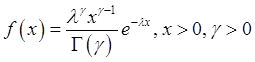 ,
, 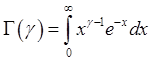 - гамма-функция
Эйлера. Описывает время безотказной работы технических устройств. При
- гамма-функция
Эйлера. Описывает время безотказной работы технических устройств. При ![]() превращается в распределение
Эрланга, применяемое в теории массового обслуживания. При
превращается в распределение
Эрланга, применяемое в теории массового обслуживания. При 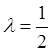 и
и 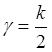 превращается в распределение
хи-квадрат
превращается в распределение
хи-квадрат ![]() , используется в
математической статистике,
, используется в
математической статистике, ![]() - степень
свободы распределения. При
- степень
свободы распределения. При ![]() превращается
в
превращается
в ![]() .
. ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.