







аксиом, то знаниями могут быть теоремы, справедливые в этой системе. При этом, используя схожесть между системами аксиом, можно преобразовать теорему в одной из систем в логическую формулу для другой системы и сделать вывод о том, что эта формула есть теорема. Т.о. аналогия используется и для решения некоторых строго сформулированных задач, и для предсказаний, а также для приобретения не заданной ранее информации.
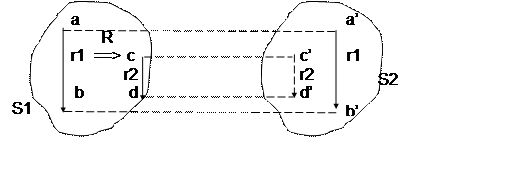
Основная гипотеза: подобие сохраняет причинные отношения, или подобные причины приводят к подобным заключениям. На рисунке a1,b1,c1,d1,a2,b2,c2,d2 – объекты, r1,r2 – отношения между объектами. В S1 r1(a1,b1) является причиной r2(c1,d1); известно, что в S2 справедливо подобное отношение r1(a2,b2).=> можно сделать вывод о существовании аналогичного отношения r2(c2,d2). Допускается существование закона перехода в причинных отношениях и использования сцепления принципа аналогии.
22. Причинно-следственные аналогии
Аналогия - это вывод подобного заключения, если справедливы подобные предпосылки. Будем считать предпосылкой и заключением причину и следствие в причинных отношениях. Основная гипотеза: подобие сохраняет причинные отношения, или подобные причины приводят к подобным заключениям. Введем обозначения: S1, S2 - некоторые множества; ai, a - факты, справедливые в S1, bj, b - факты, справедливые в S2; j - отношение между объектами, определяющее подобность (подобие).ai,j,bj - ситуация, при котором тождественность предпосылок можно рассматривать как подобие j. Тогда аналогия – это вывод b в S2, что ajb. Для строгого определения аналогии необходимо задать: определение подобия j; метод получения j из заданных объектов S1 и S2; операцию для вывода b, что ajb. Принцип аналогии проиллюстрирован рисунком:
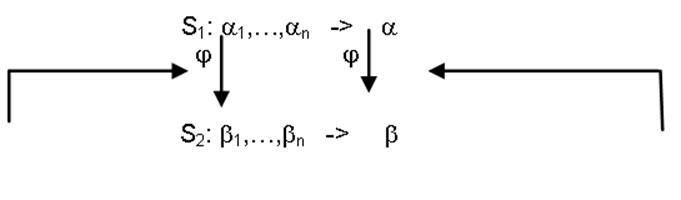
Подобие между причинами подобие между следствиями
23. Теория аналогий. Аналогия на основе парного соответствия. Правила вывода по аналогии.
Аналогия - это вывод подобного заключения, если справедливы подобные предпосылки. Введем обозначения: S1, S2-некоторые множества; aj, a - факты, справедливые в S1, bj, b - факты, справедливые в S2; j - отношение между объектами, определяющее подобность (подобие). ajjbj - ситуация, при которой тождественность предпосылок можно рассматривать как подобие j. Тогда аналогия – это вывод b в S2, что ajb. Для строгого определения аналогии необходимо задать: определение подобия j; метод получения j из заданных объектов S1 и S2; операцию для вывода b, что ajb.
Термы, не содержащие переменных в Sj, представляют собой отдельные элементы объектов, предикаты р-отношения между элементами. Пусть U(Sj) - множество термов, не содержащих переменных в Sj. Тогда парным соответствием называется конечное множество j, что j Í U(S1) x U(S2) .(x означает прямое произведение).
Пусть в S1 факты b1,…,bn служат условиями того, что факт a справедлив, а именно: в S1 справедливо aßb1,…,bn. Тогда, если существует факт bi` в S2,что bijbi`,то в S2 выводится атом a`,что aja`.
Для определения атома a`, который можно вывести по аналогии, из правила R: aßb1,…,bn с помощью j построим правило R`: a`ßb1`,…,bn`
Затем рассмотрим вывод a` из a`ßb1`,…,bn` и из известных фактов b1`,…,bn` с помощью правила модус-поненс. Построение R` из R называется преобразованием правила (на основе j), а процесс вывода a` обозначается следующей графической формой:
Конкретизация: AßB1,…,Bn
Преобразование правила с помощью j:
aßb1,…,bn
----------------a`ßb1`,…,bn`
Модус-поненс:
b1`,…,bn`, a`ßb1`,…,bn`
----------------------a`
Здесь конкретизация и модус-поненс – это выводы в дедуктивной системе, поэтому если в этой системе можно будет реализовать преобразование правила, то будет возможно использовать аналогию и дедукцию.
24. Аналогия и дедукция. Сумма аналогий
Аналогия - это вывод подобного заключения, если справедливы подобные предпосылки. Случай парного отношения j можно считать дедукцией.
Пусть S1,S2 - некоторые множества. Сумма аналогий - это ограниченное множество правил, состоящее из следующих подмножеств: R1 - множество правил, определяющих парное соответствие j; R2 - множество копий S1, S2; R3 - множество правил, выполняющих преобразование правил.
Введем предикат ~. Для каждого элемента (t1, t2), принадлежащего j, имеет место t1~t2 (1).
Для функции f, существующей одновременно в S1, S2, f(x1,…,xn)~f(y1,…,yn)ßx1~y1,…,xn~yn (2). P(j) - это множество, состоящее из правил (1) и (2).
Построим копии Si. Чтобы подчеркнуть принадлежность каждого предиката р множеству Si, присвоим ему индекс i и будем писать pi. Тогда Copy(Si) - это множество правил, которые дают возможность применить эту операцию к Si.
Правила, которые делают выводы, основанные на преобразованиях правил, можно задать, используя предикат ~ и введенный предикат присвоения индексов copy(Si). Для каждого правила в множестве S1
p(t1,…,tn)ß…,q(s1,…,sn),…
Построим новое правило суммы аналогий, состоящее из правил p2(W1,…,Wn)ß…,t1~W1,…,tn~Wn,
s1~V1,…,sn~Vn,
q1(s1,…,sn),
q2(V1,…,Vn). (3)
Для каждого правила в мн-ве S2
p(t1,…,tn)<-…,q(s1,…,sk),…
Построим новое правило суммы аналогий, состоящее из правил p1(W1,…,Wn)ß…,W1~t1,…,Wn~tn,
V1~s1,…,Vk~sk,
Q2(s1,…,sk),
Q1(V1,…,Vk). (4)
Сумма аналогий для парного соответствия j между
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.