Построение дискретных оптимальных планов эксперимента

МО РФ

НГТУ

Лабораторная работа № 4

По дисциплине

«планирование и анализ эксперимента»

вариант 6

Факультет ПМИ

Группа ПМ-12

Студенты Колесникова Л.Л.

Арьянова Е.А.

Преподаватель Лисицын Д.В.

Новосибирск, 2005г.

ПОСТРОЕНИЕ ДИСКРЕТНЫХ ОПТИМАЛЬНЫХ ПЛАНОВ ЭКСПЕРИМЕНТА

6. Модель кубическая на кубе со сторонами [–1, +1]. Строить - оптимальные планы. Алгоритм Митчелла.

1) Выберем оптимальную сетку. Для этого зафиксируем некоторый план эксперимента и будем изменять плотность сетки и фиксировать значения функционала качества:    

Так как данный функционал качества необходимо максимизировать, то в качестве оптимальной сетки выберем сетку, содержащую 275 узлов.

На выбранной сетке простроим ряд планов с разным количеством наблюдений и рассмотрим зависимость значений функционала качества критерия D-оптимальности от количества наблюдений в эксперименте.

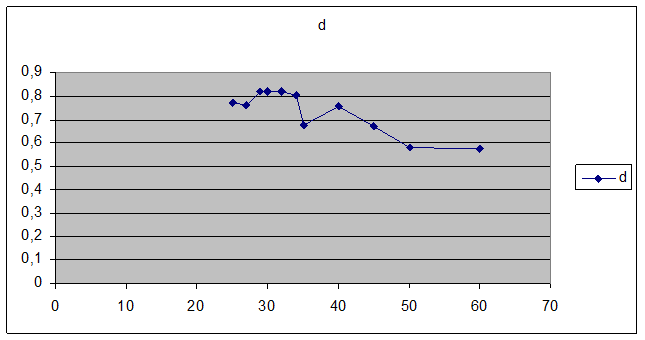
В качестве оптимального количества наблюдений выбираем 31. Построим график зависимости значений функционала качества критерия D-оптимальности от количества наблюдений в эксперименте:

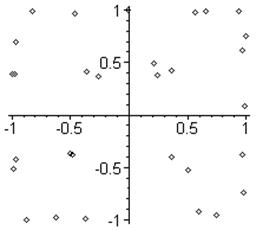
Точки оптимального плана распределены следующим образом:

Текст программы:

> restart:

> with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

> N_points:=31;N_free:=275;

> free:=array(1..N_free,1..2): eps:=array(1..N_points,1..2):

> for i to N_free do free[i,1]:=stats[random,uniform[-1,1]](1);free[i,2]:=stats[random,uniform[-1,1]](1);od:

> for i to N_points do eps[i,1]:=stats[random,uniform[-1,1]](1);eps[i,2]:=stats[random,uniform[-1,1]](1);od:

> f:=vector([1,x1,x2,x1^2,x2^2,x1^3,x2^3]);

> xmax:=array(1..2):xmin:=array(1..2):

> M:=matrix([[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0]]):for i to N_points do f1:=vector([1,eps[i,1],eps[i,2],eps[i,1]^2,eps[i,2]^2,eps[i,1]^3,eps[i,2]^3]) ;A:=multiply(f1,transpose(f1)); M:=evalm(M+A/N_points); od:D_opt:=evalf[7](det(M));

> for k to 1000 do M:=matrix([[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0]]):for i to N_points do f1:=vector([1,eps[i,1],eps[i,2],eps[i,1]^2,eps[i,2]^2,eps[i,1]^3,eps[i,2]^3]) ;A:=multiply(f1,transpose(f1)); M:=evalm(M+A); od:d:=multiply(transpose(f),inverse(M),f); xmax[1]:=free[1,1]: xmax[2]:=free[1,2]:imax:=1:dmax:=subs(x1=xmax[1],x2=xmax[2],d):for i to N_free do d1:=subs(x1=free[i,1],x2=free[i,2],d); if(d1>dmax) then dmax:=d1; xmax[1]:=free[i,1]; xmax[2]:=free[i,2];imax:=i: fi: od:   f1:=vector([1,xmax[1],xmax[2],xmax[1]^2,xmax[2]^2,xmax[1]^3,xmax[2]^3]):A:=multiply(f1,transpose(f1)): M:=evalm(M+A):  d:=multiply(transpose(f),inverse(M),f): xmin[1]:=free[1,1]: xmin[2]:=free[1,2]:dmin:=subs(x1=xmin[1],x2=xmin[2],d):imin:=1:for i to N_points do d1:=subs(x1=eps[i,1],x2=eps[i,2],d); if(d1<dmin) then dmin:=d1; xmin[1]:=free[i,1]; xmin[2]:=free[i,2]:imin:=i; fi: od:  if(xmax[1]=xmin[1] and xmax[2]=xmin[2]) then break; else free[imax,1]:=xmin[1]: free[imax,2]:=xmin[2]: eps[imin,1]:=xmax[1]: eps[imin,2]:=xmax[2]: fi: od:                                

> print("iter",k);print(xmin,xmax);

M:=matrix([[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,0,0]]):for i to N_points do f1:=vector([1,eps[i,1],eps[i,2],eps[i,1]^2,eps[i,2]^2,eps[i,1]^3,eps[i,2]^3]) ;A:=multiply(f1,transpose(f1)); M:=evalm(M+A/N_points); od:D_opt:=evalf[7](det(M));