Подбор оптимального прогноза для коррекции

Министерство Образования Российской Федерации

Новосибирский Государственный Технический Университет

Расчётно-графическая работа № 1

по курсу “Дифференциальные уравнения”

Факультет: ПМИ

Группа: ПМ-12

Студент: Сорокин А.А.

Преподаватель: Иткина Н.Б.

Вариант: 15

Новосибирск 2003

Задание.

Для коррекции  подобрать оптимальный прогноз. Обосновать выбор.

Решение.

Рассмотрим задачу Коши:

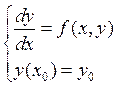
Для решения такой задачи можно применять метод “прогноза-коррекции“. Предположим, что f(x,y) – функция, непрерывная по y.

1.  Рассмотрим коррекцию вида:

                                   (1)

Предположим, что данная коррекция имеет 3-й порядок аппроксимации, т.е. . Из этого следует, что коррекция должна давать точное решение на полиномах степени 2. В качестве такого полинома, для определения коэффициентов, можно выбрать . Подставим этот полином в исходную коррекцию:

Приравняв коэффициенты в правой и левой частях при соответствующих степенях , получим систему для определения коэффициентов:

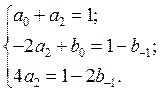
Если выбрать  в качестве параметра, то решение данной системы будет выглядеть следующим образом:

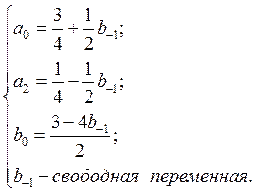                                              (2)

Получили однопараметрическое семейство коррекций.

Исследуем его на устойчивость, для чего составим уравнение для погрешности. Пусть , где  y_n – точное решение задачи в узле сетки, а u_n – численное решение. Очевидно, что помимо (1) выполняется также

, где e_n – погрешность вычисления ( при ), поэтому уравнение для погрешности будет выглядеть следующим образом:

.

Значени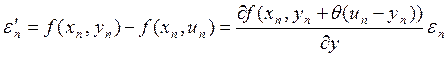е , где  (по теореме о среднем значении функции, поскольку по условию f(x,y) непрерывна по y). Т.к. шаг интегрирования  достаточно мал, то можно предположить, что величины  и 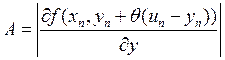 – постоянны. Получили уравнение:

Его решение ищем в виде . Получим

.

Поскольку неоднородность задачи не влияет на устойчивость, то перейдём к однородному уравнению:

.

Поделив его на , получим:

.

Корни данного уравнения проблематично найти, поэтому исследуем его на асимптотическую устойчивость (). При этом  тоже.

Перейдём к уравнению

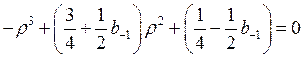.                                   (3)

Корень этого уравнения , поэтому поделим (3) на :

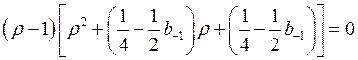.                         (4)

Уравнение (4) имеет следующие корни:

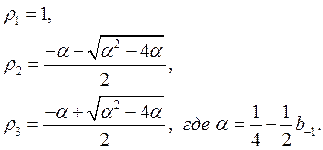                                 (5)

Для устойчивости необходимо, чтобы  .

Видим, что[1]

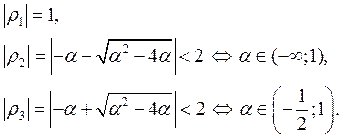                             (6)

Из (6) с учетом (5) получим ограничения на :

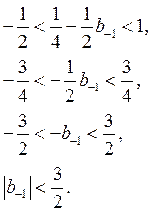                                                                (7)

Получили, что коррекция (1) будет асимптотически условно устойчивой.

2.  Теперь определим прогноз для данной коррекции. Этот прогноз будет иметь вид:

                 (8)

Аналогичным образом построим семейство коррекций и проведём его исследование на устойчивость.

Для этого положим  и для функции  получим уравнение:

Далее перейдём к системе для определения коэффициентов:

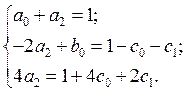
Выберем  в качестве параметров:

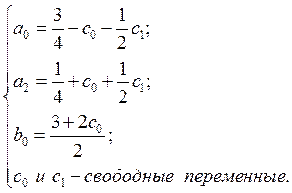                                       (9)

Имеем двухпараметрическое семейство прогнозов.

Аналогично уравнению для погрешности коррекции запишем уравнение для погрешности прогноза и исследуем на устойчивость полученное семейство:

.

Его решение ищем в виде . Получим

.

Поскольку неоднородность задачи не влияет на устойчивость, то перейдём к однородному уравнению:

.

Поделив его на , получим:

.

Корни данного уравнения проблематично найти, поэтому исследуем его на асимптотическую устойчивость ().

Перейдём к уравнению

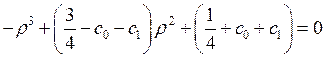                                (10)

Корень этого уравнения , поэтому поделим (10) на :

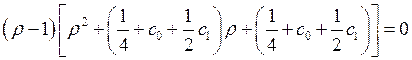.              (11)

Уравнение (11) имеет следующие корни:

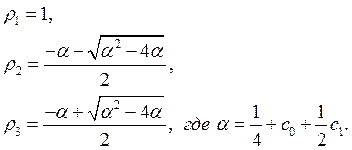                           (12)

Для устойчивости необходимо, чтобы  .

Видим, что[2]

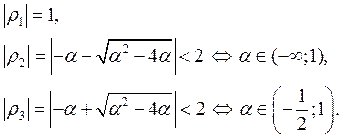                             (13)

Из (13) с учетом (12) получим ограничения на :

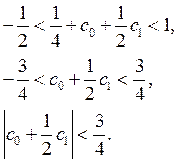                                                           (14)

Получили, что прогноз (8) будет асимптотически условно устойчивым.

Исследования.

Для нахождения оптимального прогноза выберем 4 пары “прогноз-коррекция” согласно условиям (7), (14) и таблице

уравнения которых, в соответствии с (2), (9) и таблицей, будут иметь вид:

1. 

.

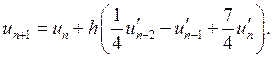
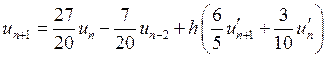2. 

.

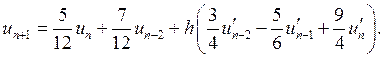
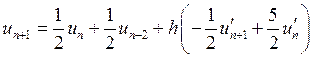3. 

.

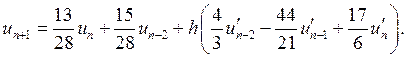
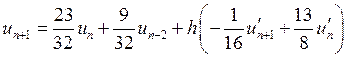4. 

.

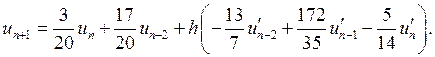
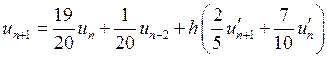Проанализируем полученные результаты. Как видно из таблиц 1, 2, 3 и 4, пары “прогноза-коррекции” по “точности” расположены в возрастающем порядке (по номеру пары). Наиболее оптимальной парой “прогноза-коррекции” является 4-ая пара. Подтвердим это разбором всех пар между собой и разбором каждой пары в отдельности.

1-ая пара уступает всем остальным парам на 2-3 порядка точности по значениям . Видимо, это связано с тем, что при выборе свободных переменных  коэффициент  обратился в 0 и, таким образом, “ушло” слагаемое  из формулы прогноза.

У 2-ой пары  составляет порядка  в зависимости от теста. Это говорит о том, что “коррекция” почти никак не корректирует “прогноз”. Поэтому значения  зависят от результата “прогноза”, который, к сожалению, хуже, чем у 3-ей и 4-ой парах. Порядок  составляет  на шаге h/4 в зависимости от теста (подробнее смотрите таблицу 2).

Результаты тестов 3-ей пары такие: на 1-м тесте  составляет порядка , что тоже говорит о том, что “коррекция” никак не корректирует “прогноз”. Но при этом “прогноз” дает значение на порядок точнее, чем аналогичное значение 2-ой пары. На 2-м тесте порядок  составляет , а порядок  составляет . Это вполне хороший результат. Результаты 3-го теста говорят нам, что “коррекция” корректирует “прогноз”, причем  составляет порядка , что почти на порядок лучше результатов 3-го теста 2-ой пары.

4-ая пара дает самые хорошие результаты (относительно первых трех пар). 1-ый тест по значениям  и  выигрывает 4-ая пара у 3-ей, т.к. уже на шаге h 4-ая пара дает точное численное решение. На 2-ом тесте значения  4-ой пары составляет порядка , что тоже говорит о точности получаемого решения. Значения же  3-ей пары в среднем на 2 порядка выше, чем у 4-ой пары. В 3-ем же тесте “коррекция” корректирует “прогноз” почти одинаково как у 3-ей, так и у 4-ой парах (по значениям ). Но значения  3-ей пары в целом ровно на порядок ниже, чем значения  4-ой пары, т.е. в этом тесте 4-ая пара “проиграла” один порядок по точности 3-ей паре (подробнее смотрите таблицы 3 и 4).

Таким образом, можем сказать, что 4-ая пара дает результаты в совокупности лучшие, чем результаты 1-ой, 2-ой и 3-ей пар.

Отметим также уменьшение значений  каждой из пар при уменьшении шага в 4 раза. 1-ая пара “уменьшает” порядок  в целом на единицу на 1-м и 2-м тестах. На 3-м тесте значения  не уменьшаются. 2-ая пара “уменьшает” порядок  на единицу на всех трех тестах. 3-ая пара “уменьшает” значение  на полтора порядка на 1-м тесте, на порядок – на 2-м тесте и почти на порядок – на 3-м тесте. В 4-ой паре порядок  держится  на 1-м тесте и  на 2-м тесте. На 3-м тесте порядок  уменьшается на треть.