Параллельные вычислительные методы

Министерство Образования и Науки РФ

НГТУ

Кафедра ПВт

Лабораторная работа №2

По дисциплине ”Параллельные вычислительные методы”

Факультет:  ПМИ

Группа: ПМ-23

Студенты:    Соболев Д.А.

Макеевская Д.О.

Казанцев А.А.

Преподаватель: Куликов И.М.

Новосибирск 2006

Задание

Разработать параллельную программу решения СЛАУ с разреженной матрицей итерационным методом. Исследовать число операций параллельного метода, определить ускорение. Билинейные функции, метод сопряжённых градиентов.

Выполнение

Метод сопряжённых градиентов:

Далее для k=1,2,… производятся следующие вычисления:

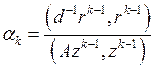
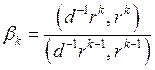
Поставим дифференциальную задачу. Будем рассматривать стационарную задачу распределения температуры в области, куда помещён инородный объект с отличной от области теплопроводности. Таким образом, решаемое уравнение имеет вид:

, в расчётной области , с областью объекта , где коэффициенты теплопроводности имеют значения:  для области,  для объекта, объект выделяет тепло с интенсивностью , краевые условия , , .

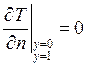В МКЭ для определения коэффициентов в разложении неизвестной функции u по базисным функциям 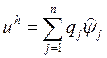 используется следующая СЛАУ

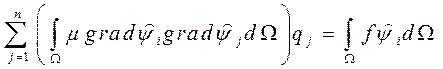
Локальная матрица жесткости: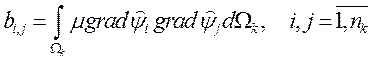    

Локальная матрица массы: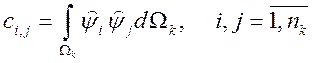   

Локальный вектор правой части:

Линейные базисные функции:

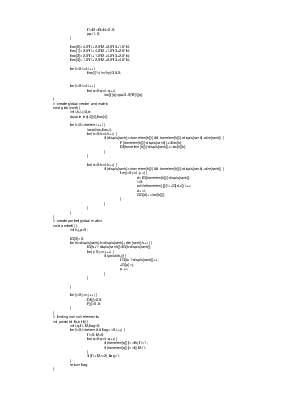
Результаты работы программы

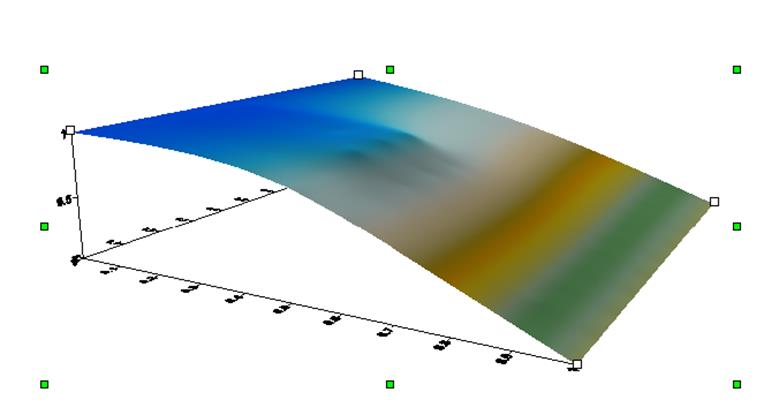
Программа

#include "mpi.h"

#include <stdio.h>

#include <math.h>

#include <stdlib.h>

#define N 1000

#define eps 1e-20

#define MAX 100

#define CH 1e+20

int size, rank,dim[10],displs[10],ost;

int IG[N],JG[N],konelem[4][N],n,kelem;

double GG[N],DI[N],F[N],uzel[3][N],pp=1.0;

int prover(int c1,int c2,int c3,int c4);

int poisk(int fk,int fj);

void ku(void);

double func(double fx,double fy) {

return 0;

}

double u(double fx,double fy) {

if (fx<eps) return 1.0;

if (fabs(fx-1.0)<eps ) return 0.0;

return 0.0;

}

// load data

void rar(void) {

int i=0;

FILE *fp;

fp = fopen("uzel4.txt","r");

if (fp==NULL) { printf("error read file uzel.txt!\n");exit(0);}

fscanf(fp,"%d",&n);

for(i=0;i<n;i++)

fscanf(fp,"%lf %lf %lf",&uzel[0][i],&uzel[1][i],&uzel[2][i]);

fclose(fp);

fp = fopen("konelem4.txt","r");

if (fp==NULL) { printf("error read file konelem.txt!\n");exit(0);}

fscanf(fp,"%d",&kelem);

for(i=0;i<kelem;i++)

fscanf(fp,"%d %d %d %d",&konelem[0][i],&konelem[1][i],&konelem[2][i],&konelem[3][i]);

fclose(fp);

}

// create local vector and matrix

void local(double loc[][4],double floc[],int i) {

int l,q,flag;

double hx,hy,B[4][4],C[4][4],f1,f2,f3,f4;

hx=fabs(uzel[0][konelem[0][i]]-uzel[0][konelem[2][i]]);

hy=fabs(uzel[1][konelem[0][i]]-uzel[1][konelem[2][i]]);

B[0][0]=B[1][1]=B[2][2]=B[3][3]=hy/hx+hx/hy;

B[1][0]=B[0][1]=B[3][2]=B[2][3]=-hy/hx+hx/(2*hy);

B[2][0]=B[0][2]=B[3][1]=B[1][3]=hy/(2*hx)-hx/hy;

B[3][0]=B[0][3]=B[2][1]=B[1][2]=-hy/(2*hx)-hx/(2*hy);

C[0][0]=C[1][1]=C[2][2]=C[3][3]=4;

C[1][0]=C[0][1]=C[3][2]=C[2][3]=2;

C[2][0]=C[0][2]=C[3][1]=C[1][3]=2;

C[3][0]=C[0][3]=C[2][1]=C[1][2]=1;

/*f1=func(uzel[0][konelem[0][i]],uzel[1][konelem[0][i]]);

f2=func(uzel[0][konelem[1][i]],uzel[1][konelem[1][i]]);

f3=func(uzel[0][konelem[2][i]],uzel[1][konelem[2][i]]);

f4=func(uzel[0][konelem[3][i]],uzel[1][konelem[3][i]]);*/

flag=prover(konelem[0][i],konelem[1][i],konelem[2][i],konelem[3][i]);

if (flag) {

f1=f2=f3=f4=10.0;

pp=10.0;

}

else {

f1=f2=f3=f4=0.0;

pp=1.0;

}

floc[0]=4.0*f1+2.0*f2+2.0*f3+1.0*f4;

floc[1]=2.0*f1+4.0*f2+1.0*f3+2.0*f4;

floc[2]=2.0*f1+1.0*f2+4.0*f3+2.0*f4;

floc[3]=1.0*f1+2.0*f2+2.0*f3+4.0*f4;

for(l=0;l<4;l++)

floc[l]*=(hx*hy)/36.0;

for(l=0;l<4;l++)

for(q=0;q<4;q++)

loc[l][q]=(pp/3.0)*B[l][q];

}

// create global vector and matrix

void glob(void) {

int i,k,l,j=0,d;

double loc[4][4],floc[4];

for(i=0;i<kelem;i++) {

local(loc,floc,i);

for(k=0;k<4;k++) {

if (displs[rank]<=konelem[k][i] && konelem[k][i]<displs[rank]+dim[rank]) {

F[konelem[k][i]-displs[rank]]+=floc[k];

DI[konelem[k][i]-displs[rank]]+=loc[k][k];

}

}

for(k=0;k<4;k++) {

if (displs[rank]<=konelem[k][i] && konelem[k][i]<displs[rank]+dim[rank]) {

for(j=0;j<4;j++) {

d=IG[konelem[k][i]-displs[rank]];

l=0;