





МО и ПО РФ
Новосибирский Государственный Технический Униерситет
Кафедра параллельных технологий
Лабораторная работа 1
по предмету: «Параллельное программирование»
Факультет: ПМИ
Группа: ПМ-93
Студенты: Ельцин В.В.
Клещенок Д.С.
Преподаватель: Медведев
Новосибирск 2003
1 Задание.
Написать программу, позволяющую решить систему уравнений методом Гаусса.
Сравнить два алгоритма.
2 Решение задачи.
Метод Гаусса представляет собой дву алгоритм, позволяющий решать линейные системы уравнений вида:
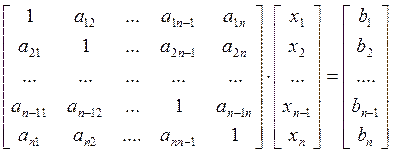
Первый шаг алгоритма - это прямой ход, позволяет получить путем линейных преобра- зований верхнетреугольную матрицу А, соответственно меняя элементы вектора В.
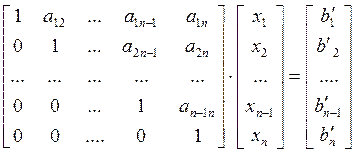
Второй шаг - обратный ход, непосредственное нахождение неизвестных компонент вектора Х.
Соответственно, в зависимости от распределения строк матрицы и вектора между процессами, существует два способа распараллеливания метода Гаусса.
Каждому процессу распределяется некоторое количество строк, идущих подряд, то есть, если имеется k процессов, то первый работает со строками от нулевой до строки с номером n/k-1 и т. д. Тогда прямой ход будет работать следующим образом: сначала каждый процесс посчитает количество строк, которые он должен принять, примет их, вычтет из своих строк, затем, каждый процесс возьмет свою первую строку, разошлет ее всем остальным последующим процессам, а из остальных своих строк ее вычтет. Так каждый процесс будет работать с каждой своей строкой. Обратный ход аналогичен, только начинается с последней строки.
Реализация этого варианта метода Гаусса представлена в первой программе
В этом случае строки распределяются по процессам циклически
В программе метод представлен следующим образом. Начиная с первой строки, по очереди, берется каждая строка и определяется, принадлежит ли она данному процессу. Если принадлежит, то ее надо разослать всем остальным процессам и вычесть из своих строк, которые следуют за ней. Если же очередная строка матрицы не принадлежит текущему процессу, то процесс должен принять ее и вычесть из своих строк. . Обратный ход аналогичен, только начинается с последней строки. Этот алгоритм реализует вторая программа.
3 Приложение
Программа 1
#include <mpi.h>
#include <stdio.h>
#include <time.h>
main(int argc,char **argv){
int rank,size,ii,jj,kk,i,j,k,j1,a,b,n=16;
float **mt,*x,*f,*s,fl,sf;
FILE *fv,*fm,*fs;
time_t start,stop;
MPI_Status st;
MPI_Init(&argc,&argv);// Initialisation MPI
MPI_Comm_rank(MPI_COMM_WORLD,&rank);
MPI_Comm_size(MPI_COMM_WORLD,&size);
fv=fopen("vect.dat","r");
fm=fopen("matr.dat","r");
fs=fopen("size.dat","r");
fscanf(fs,"%d",&n);
close(fs);
a=n/size;
b=n%size;
if(b){
if(rank<b){
k=a+1;
kk=rank*(a+1);
}else{
k=a;
kk=b*(a+1)+(rank-b)*a;
}
}else{
k=a;
kk=rank*a;
};
x=(float *)malloc(sizeof(float)*n);
f=(float *)malloc(sizeof(float)*n);
s=(float *)malloc(sizeof(float)*n);
mt=(float **)malloc(sizeof(float*)*k);
for(i=0;i<k;i++)mt[i]=(float *)malloc(sizeof(float)*n);
/*--------------------------------------------------------*/
for(i=0;i<kk;i++){
fscanf(fv,"%f",&fl);
for(j=0;j<n;j++)fscanf(fm,"%f",&fl);
}
for(i=0;i<k;i++){
fscanf(fv,"%f",&f[i]);
for(j=0;j<n;j++)fscanf(fm,"%f",&mt[i][j]);
}
close(fv);
close(fm);
start=time(0);
/*---------------------prjamoy-----------------------------*/
for(i=0;i<kk;i++){
MPI_Recv(s,n,MPI_FLOAT,MPI_ANY_SOURCE,15,MPI_COMM_WORLD,&st);
MPI_Recv(&sf,1,MPI_FLOAT,MPI_ANY_SOURCE,16,MPI_COMM_WORLD,&st);
for(ii=0;ii<k;ii++){
fl=mt[ii][i];
f[ii]-=sf*fl;
for(j=0;j<n;j++)mt[ii][j]-=s[j]*fl;
}
}
for(i=0;i<k;i++){
fl=1.0/mt[i][kk+i];
f[i]*=fl;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.