Оценка параметров и проверка гипотез в линейных моделях с качественными факторами

МО РФ

НГТУ

кафедра программных систем и баз данных

Лабораторная работа N1

по дисциплине «Планирование и анализ экспериментов»

на тему «Оценка параметров и проверка гипотез в линейных моделях

с качественными факторами».

Факультет:           ПМИ

Группа:                 ПМ – 91

Студенты:             Игонина А.С.

Пахомов А.В.

Преподаватель:    Попов А.А.

Лисицын Д.В.

Вариант:               5

 Новосибирск 2003

1. Задание

По имеющимся данным составим матрицу наблюдений X:

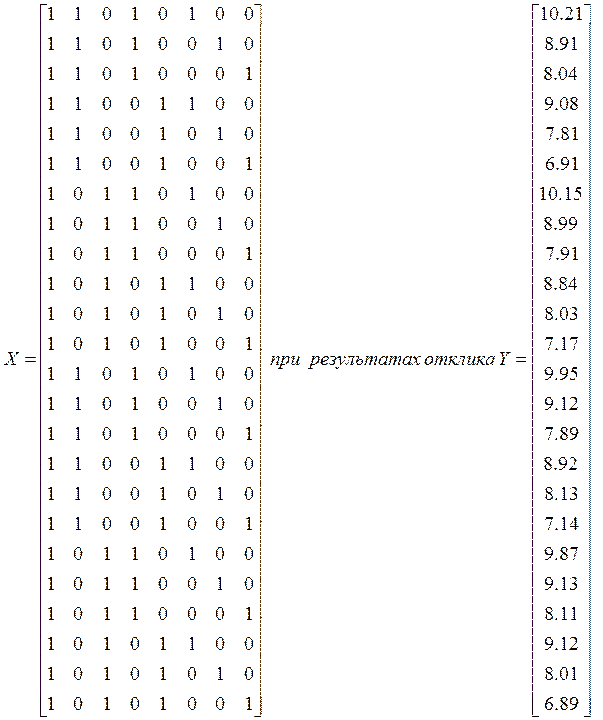
Вектор неизвестных параметров

Модель  является моделью дисперсионного анализа с главными эффектами, без взаимодействий уровней факторов.

2. Вычисление оценок редуцированной модели

Матрица наблюдений редуцированной модели

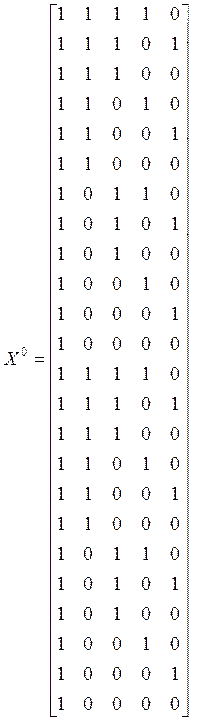
В базис ФДО войдут следующие:

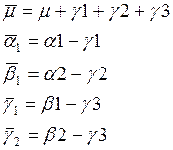
Найдем МНК оценку ФДО в редуцированной модели:

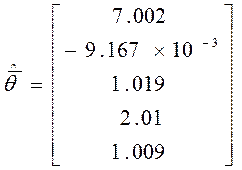
Следовательно, оценка векторов неизвестных параметров ПФЭ:

3. Проверка гипотез о незначимости вида.

Для вычисления статистик понадобится оценка дисперсии ошибки:

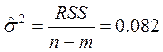
Для первого фактора:

Гипотеза о незначимости различий 1-го и 2-го уровней

H₁:=0

Значение статистики F=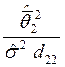=6.164*10^-3>F_0.05,1,24-5=4.037*10^-3

Следовательно, гипотеза H₁ отвергается.

Для второго фактора:

Гипотеза о незначимости различий 1-го и 2-го уровней

H₁: =0

Значение статистики F==76.192>F_0.05,1,24-5=4.037*10^-3

Следовательно, гипотеза H₁ отвергается.

Для третьего фактора:

Гипотеза о незначимости различий 1-го и 3-го уровней

H₁: =0

Значение статистики F==197.569>F_0.05,1,24-5=4.037*10^-3

Следовательно, гипотеза H₁ отвергается.

Гипотеза о незначимости различий 2-го и 3-го уровней

H₂: =0

Значение статистики F==49.761>F_0.05,1,24-5=4.037*10^-3

Следовательно, гипотеза H₂ отвергается.

Гипотеза о незначимости различий 1-го и 2-го уровней

H₃:=

Значение статистики F=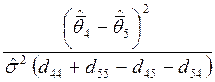=49.024>F_0.05,1,24-5=4.037*10^-3

Следовательно, гипотеза H₃ отвергается.

Гипотеза о незначимости кривизны линий зависимости Y от фактора

H₄:-2=0

При с=(0 0 0 1 -2)^T, значение статистики F=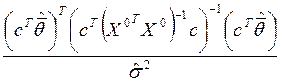=9.169*10^-4<F_0.05,1,24-5=4.037*10^-3

Следовательно, гипотеза H₄ принимается.

5. Выводы:

Проверенные гипотезы дают следующие результаты:

1.  Первый фактор значимо влияет на вариацию отклика Y.

2.  Второй фактор значимо влияет на вариацию отклика Y.

3.  Третий фактор значимо влияет на вариацию отклика Y.

4.  Различие в уровнях третьего фактора существенно.

5.  Кривизна линий зависимости Y от третьего фактора не существенна.