Оценивание линейных регрессионных моделей в условиях гетероскедастичности возмущений

Н О В О С И Б И Р С К И Й    Г О С У Д А Р С Т В Е Н Н Ы Й

Т Е Х Н И Ч Е С К И Й   У Н И В Е Р С И Т Е Т

Кафедра прикладной математики

и

информатики

Лабораторная работа №2а

по курсу

«Статистические методы

анализа данных»

Тема:

«Оценивание линейных регрессионных моделей в

условиях гетероскедастичности возмущений»

          Группа: ПМ – 71

Студентки: Дружилова Елена

Молоканова Татьяна

Вариант: №1

Новосибирск 2000 г.

Задание: Дисперсия возмущений – возрастающая функция от одного фактора (квадрат фактора).

Имитационная модель имеет вид:

y=-1.5+2*x1+0.001*x1*x1+4*x2-9*x2*x2

1.  Провести моделирование регрессионного процесса с гетероскедастичным возмущением:

Для моделирования данного процесса была написана программа на языке С:

#include <stdio.h>

#include <conio.h>

#include <stdlib.h>

#include <string.h>

#include <math.h>

#define Pi  3.14159265

#define M 5

#define N 12

#define ro 0.075

const float t[M]={-1.5,2,0.001,4,-9};

const float x1[N]={-0.75,-0.75,-0.75,-0.25,-0.25,-0.25,0.25,0.25,0.25,0.75,0.75,0.75,};

const float x2[N]={-0.8,0,0.8,-0.8,0,0.8,-0.8,0,0.8,-0.8,0,0.8};

float Sigma (float u[],float u_mean);

float e_j (float sigma);

float Sign (float var);

void main()

{

int i=0;

FILE* res;

float u[N],u_mean=0,sigma,y[N],k;

clrscr();

res=fopen("res.dat","w");

while (i<N)

{

u[i]=t[0]+t[1]*x1[i]+t[2]*x1[i]*x1[i]+t[3]*x2[i]+t[4]*x2[i]*x2[i];

u_mean+=u[i];

i++;

}

u_mean/=N;

sigma=Sigma(u,u_mean);

for (i=0;i<N;i++)

{       k=e_j(sigma);

y[i]=u[i]+k;

}

for (i=0;i<N;i++)

{

fprintf (res,"%f %f %f %f\n",x1[i],x2[i],u[i],y[i]);}

fprintf (res,"\n");

fclose (res);

}

float Sigma (float u[],float u_mean)

{

FILE *sigm;

float s1=0,s;

for (int i=0;i<N;i++)

{s1+=(u[i]-u_mean)*(u[i]-u_mean);}

for (i=0;i<N;i++)

{

s=x1[i]*x1[i];

sigm=fopen("sigma.dat","a");

fprintf (sigm,"\n%f",s*s);

}

fclose (sigm);

return (s);

}

float e_j (float sigma)

{

float ksi,e;

ksi=1.0*random(1000)/1000;

e=sigma*Sign(2*ksi-1)*sqrt(-0.5*Pi*log(4*ksi*(1-ksi)));

return e;

}

float Sign (float var)

{

if (var>0) return (1);

if (var<0) return (-1);

return (0);

}

В результате которой были получены следующие данные:

X1	X2	U	y	Sigma
-0.750000 -0.750000 -0.750000 -0.250000 -0.250000 -0.250000 0.250000 0.250000 0.250000 0.750000 0.750000 0.750000	-0.800000 0.000000 0.800000 -0.800000 0.000000 0.800000 -0.800000 0.000000  0.800000  -0.800000 0.000000  0.800000	-11.959437 -2.999438 -5.559438 -10.959938 -1.999938 -4.559937 -9.959938 -0.999937 -3.559938 -8.959437 0.000563 -2.559438	-13.226248 -4.482574 -5.798821 -11.971422 -2.208890 -4.998045 -9.909113 -1.480870 -3.265565 -8.056066 -0.336462 -2.638646	0.316406 0.316406 0.316406 0.316406 0.003906 0.003906 0.003906 0.003906 0.003906 0.003906 0.316406 0.316406

2.  Проверка полученных данных по тестам на гетероскедастичность:

Тест Брейча–Пагана:

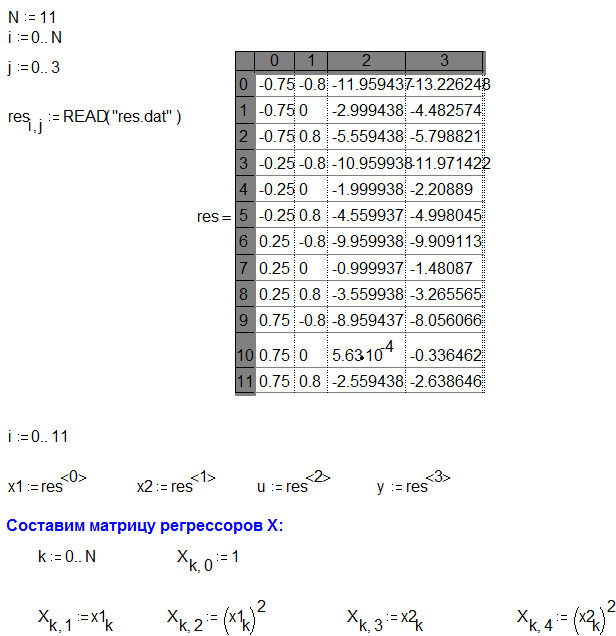
В этом тесте исходное уравнение наблюдений оценивается по МНК и в оболочке модели отыскивается вектор остатков:

e_t= y_t – ¦^т(x_t)*q, где t- индекс наблюдения, затем формируется отклик и строится регрессия по факторам и затем рассчитывается RSS, по которой затем и проверяется гипотеза о гетероскедастичности модели: 1/2RSS ~ c²(p).

Для проверки данных по тесту Брейча-Пагана быоа составлена программа в математическом пакете MATHCAD.

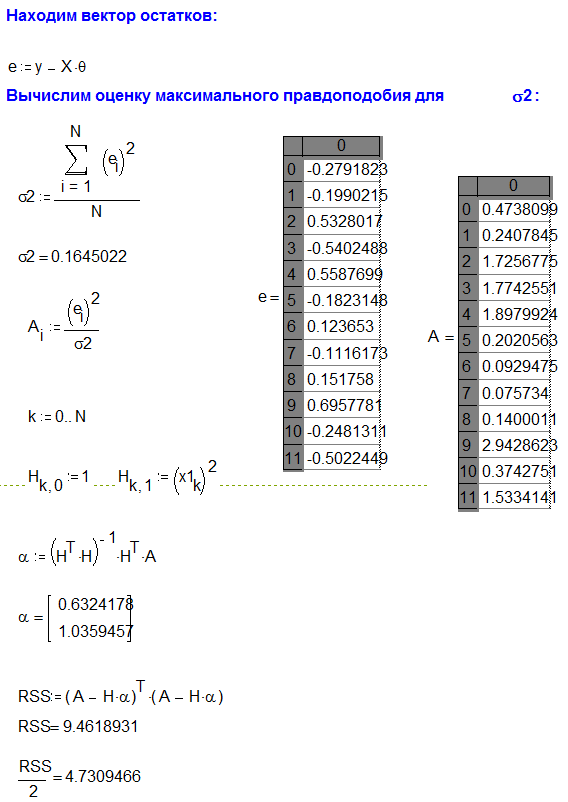В данном случае p=1.

RSS/2=4.7309466

c²= 3.84

Т.к. RSS/2 > c²

Следовательно модель гетероскедастична.

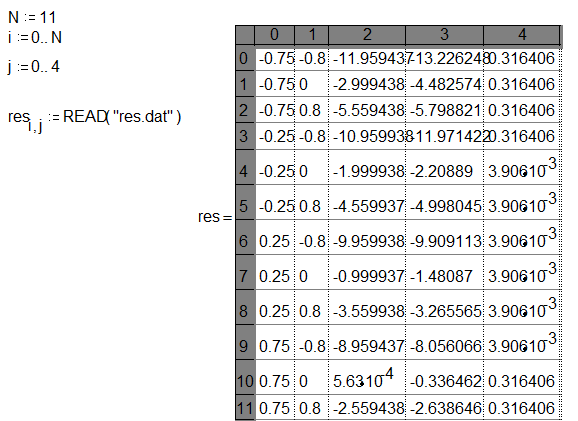
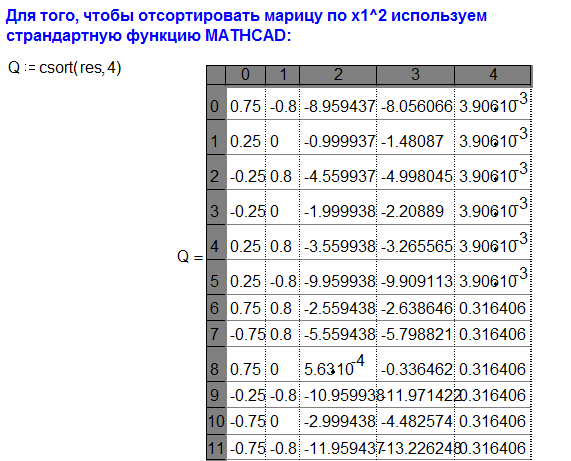
Тест Голдфельда–Квандтона:

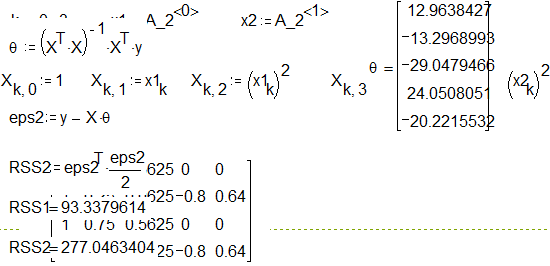RSS2/RSS1=2.968206464

Оценивание параметров регрессионной модели по

обобщенному МНК и обыкновенному МНК:

q_ист=(-1.5,2,0.001,4,-9)

Сравнить эффективность оценок в этих случаях

(при расчетах использовать истинные значения параметров):