



Министерство Образования Российской Федерации
кафедра прикладной математики
Факультет: ПМИ
Группа: ПМ-91
Студент: Кучеров Д.А.
Преподаватель: Цой Е.Б.
2003
1. Моделирование равномерно распределённой случайной величины (физический генератор).
Примером такой генерации может быть, например, процесс бросания правильного многогранника (куб, додекаэдр, икосаэдр) с нанесёнными на грани числами 1, 2,…, N (где N – число граней) на горизонтальную поверхность. Считывание числа производится по нижней грани. Вероятность выпадения некоторого числа равна 1/N. Таким образом, распределение случайной величины будет равномерным на дискретном множестве {1, 2,…, N}.
2.Написать
алгоритм моделирования дискретной величины гипергеометрического распределения: 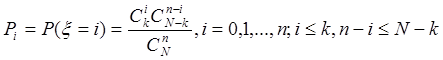
Моделирование такой величины можно осуществить по следующей схеме:
В
этом алгоритме осталось вычислить величину ![]() ,
которая выражается с помощью следующей формулы:
,
которая выражается с помощью следующей формулы: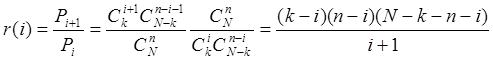 .
.
3. Найти методом обратной функции моделирующее
выражение для случайной величины ![]() , имеющей заданную
плотность распределения.
, имеющей заданную
плотность распределения.
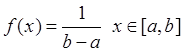 . Вычислим функцию распределения
. Вычислим функцию распределения 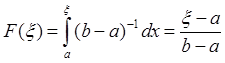 . После разрешим уравнение
. После разрешим уравнение ![]() , где
, где ![]() ,
относительно
,
относительно ![]() . В результате будем иметь моделирующее
выражение для случайной величины
. В результате будем иметь моделирующее
выражение для случайной величины ![]() с плотность
с плотность ![]() :
:
![]() .
.
4. Найти моделирующее выражение для случайной величины ![]() , имеющей заданную плотность распределения,
по методу обратной функции, когда
, имеющей заданную плотность распределения,
по методу обратной функции, когда ![]() немонотонна.
немонотонна.
![]()
Вычислим константу c, которая
равна с=3e/(1+3e) . Разобьем нашу исходную функцию плотности на две функции ![]() и
и ![]() .
Естественно положить
.
Естественно положить 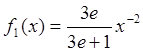 , а
, а 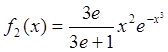 .
После этого можно вычислить соответствующие вероятности:
.
После этого можно вычислить соответствующие вероятности: 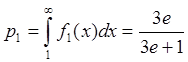 и аналогично вычислим
и аналогично вычислим
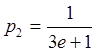 .
Теперь необходимо найти для каждой функции ее распределение, которое
вычисляется по определению.
.
Теперь необходимо найти для каждой функции ее распределение, которое
вычисляется по определению. 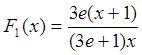 и
и 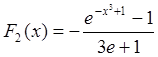
. Последовательно разрешая уравнения ![]() относительно
относительно ![]() ,
получаем моделирующие выражения на определенном интервале. Результат можно
представить в следующей форме:
,
получаем моделирующие выражения на определенном интервале. Результат можно
представить в следующей форме:
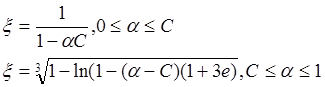 .
.
5. Написать алгоритм моделирования случайной величины ![]() распределенной по закону
распределенной по закону ![]() , с использованием порядковых статистик.
, с использованием порядковых статистик.
![]() . Первым делом необходимо вычислить параметр
c, исходя из
того, что
. Первым делом необходимо вычислить параметр
c, исходя из
того, что 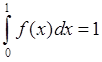 . Проинтегрировав и разрешив уравнение
относительно c, получим, что
. Проинтегрировав и разрешив уравнение
относительно c, получим, что ![]() .
Поскольку существуют отрицательные коэффициенты при степенях x,
то воспользуемся полиномом Бернштейна. При этом стоит отметить, что плотность
распределения k-ой порядковой статистики равномерно распределенной
имеет вид:
.
Поскольку существуют отрицательные коэффициенты при степенях x,
то воспользуемся полиномом Бернштейна. При этом стоит отметить, что плотность
распределения k-ой порядковой статистики равномерно распределенной
имеет вид: ![]() . Преобразуем исходную плотность к
следующему виду
. Преобразуем исходную плотность к
следующему виду ![]() . Теперь определим коэффициенты
полинома Бернштейна:
. Теперь определим коэффициенты
полинома Бернштейна:
![]() 1. k=3 n =4
1. k=3 n =4 ![]()
![]() 2. k=2
n =3
2. k=2
n =3 ![]()
![]() 3. k=1
n =2
3. k=1
n =2 ![]()
Перепишем
по-новому функцию распределения 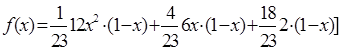 . Тогда можно выписать
порядковые статистики и их вероятности.
. Тогда можно выписать
порядковые статистики и их вероятности.
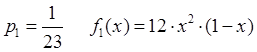
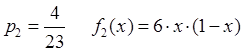
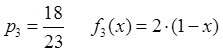
6. Написать алгоритм моделирования случайной величины ![]() по методу исключения.
по методу исключения.
![]() . Параметр
. Параметр ![]() . Для
моделирования случайной величины необходимо задаться постоянной
. Для
моделирования случайной величины необходимо задаться постоянной ![]() , удовлетворяющей
, удовлетворяющей ![]() .
Можно положить
.
Можно положить ![]() .
.
Тогда алгоритм моделирования можно записать следующим образом:
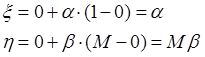
7. Написать алгоритм моделирования случайной величины ![]() , имеющей указанную плотность
распределения.
, имеющей указанную плотность
распределения.
![]() .
.
Вычислим
константу c, которая равна 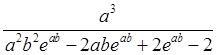 .
Воспользуемся методом исключения. Для моделирования случайной величины
необходимо задаться постоянной
.
Воспользуемся методом исключения. Для моделирования случайной величины
необходимо задаться постоянной ![]() , удовлетворяющей
, удовлетворяющей ![]() . Поскольку функция f(x) возрастающая, то на отрезке [a,b] она будет иметь максимуму в точке b.
Следовательно, в качестве M можно будет взять любое число большее f(b), например, M=f(b)+1. После этого можно воспользоваться алгоритмом
моделирования, описанного в предыдущем примере.
. Поскольку функция f(x) возрастающая, то на отрезке [a,b] она будет иметь максимуму в точке b.
Следовательно, в качестве M можно будет взять любое число большее f(b), например, M=f(b)+1. После этого можно воспользоваться алгоритмом
моделирования, описанного в предыдущем примере.
8. Написать алгоритм моделирования случайной величины ![]() при помощи метода суперпозиции.
при помощи метода суперпозиции.
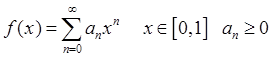 .
.
Преобразуем
нашу функцию плотности к следующему виду: 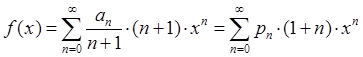 , где
, где 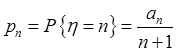 . Запишем условную плотность распределения
. Запишем условную плотность распределения ![]() . Теперь составим уравнение относительно
. Теперь составим уравнение относительно ![]() , которое имеет вид:
, которое имеет вид: 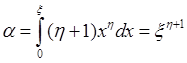 . Отсюда можно получить моделирующее
выражение для случайной величины
. Отсюда можно получить моделирующее
выражение для случайной величины ![]() :
: ![]() , где
, где ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.