Моделирование равномерно распределенной случайной величины. Анализ решения задачи

Министерство Образования Российской Федерации

Новосибирский Государственный Технический Университет

Лабораторная работа по

методам  моделирования №1

Факультет: ПМИ

Группа: ПМ-81

Студенты: Головина Н., Берязев И.

Преподаватели: Тишковская С. В.,Тимофеев В.С.

г. Новосибирск-2001

Цель работы: Моделирование равномерно распределенной случайной величины на  отрезке (0,1).

Условие задачи: Для заданного объема выборки N построить элементы выборки x₁,…,x_N  принадлежащие Rav(0,1).

Анализ решения задачи:

Для построения заданной выборки использовались следующие методы:

1. x_n+1=(ax_n+c) mod m ,где x₀ >=0, a>0, c>=0, m=1,2,…
2. x_n+1=(bx²_n+ax_n+c) mod m ,где x₀ >=0, a>0, c>=0, b>0, m=1,2,…
3. x_n+1=(x_n+x_n-1) mod 4, где x₀=3,1415927, x₁>0.
4. Стандартный счётчик (random).

 В первых 3 способах,  дополнительное деление на m x_n+1элемента выборки, в четвертом методе сначала задается порядок случайных величин - е, числа генерируются на интервале (0, 10^е), а затем полученные элементы делятся на число  10^е.

Результаты:

Метод 1:

1) x0=1 a=2 c=3 m=4 n=10

0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25

2)x0=5 a=2 c=1 m=9 n=10

0.222222 0.555556 0.222222 0.555556 0.222222 0.555556 0.222222 0.555556 0.222222 0.555556

Исследования:

метод 1:x0=1 a=15 c=18 m=289 n=160

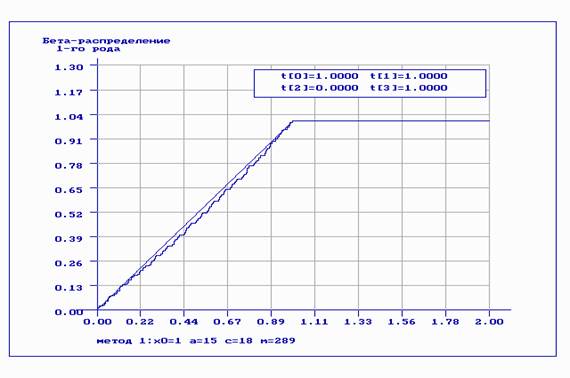
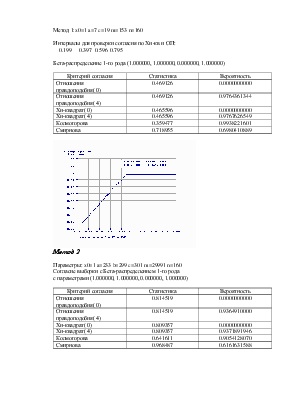
Интервалы для проверки согласия по Хи-кв и ОП:

0.199  0.399  0.598  0.797

Бета-распределение 1-го рода (1.000000, 1.000000, 0.000000, 1.000000)

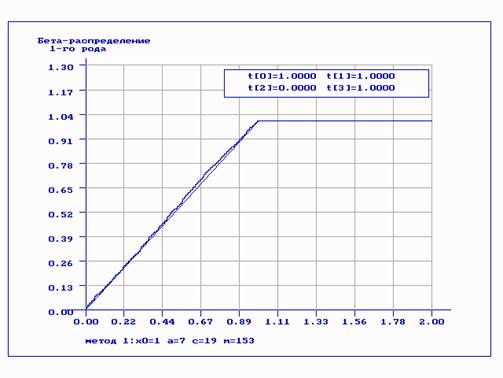
Метод 1:x0=1 a=7 c=19 m=153 n=160

Интервалы для проверки согласия по Хи-кв и ОП:

0.199  0.397  0.596  0.795

Бета-распределение 1-го рода (1.000000, 1.000000, 0.000000, 1.000000)

Метод 2

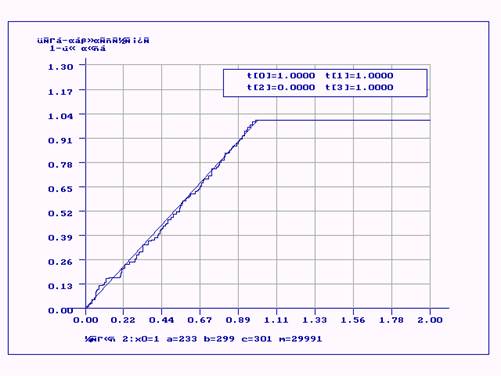
Параметры: x0=1 a=233 b=299 c=301 m=29991 n=160

Cогласие выборки с Бета-распределением 1-го рода

с параметрами (1.000000, 1.000000, 0.000000, 1.000000)

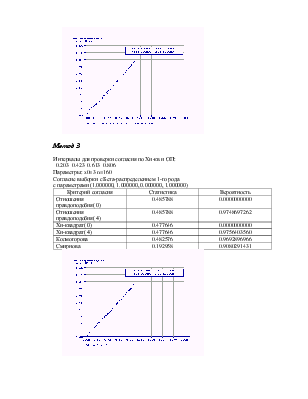
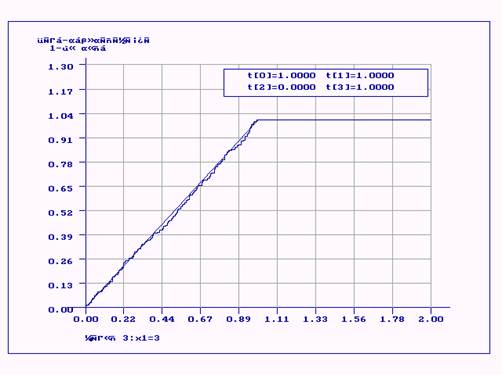
Метод 3

Интервалы для проверки согласия по Хи-кв и ОП:

  0.203  0.423  0.613  0.806

Параметры: x0=3 n=160

Cогласие выборки с Бета-распределением 1-го рода

с параметрами (1.000000, 1.000000, 0.000000, 1.000000)

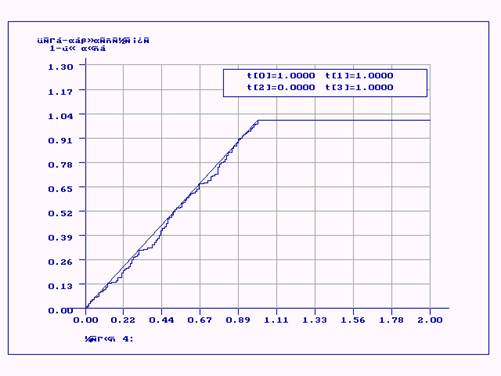
Метод 4

Интервалы для проверки согласия по Хи-кв и ОП:

0.225  0.440  0.605  0.820

Параметры: x0=3 n=160

Cогласие выборки с распределением:

Бета-распределение 1-го рода (1.000000, 1.000000, 0.000000, 1.000000)

Линейная конгруэнтная последовательность вида x_n+1=(ax_n+c)mod m

 имеет длину периода m тогда и только тогда, когда

1. c и m взаимно простые числа;

2. c < m, a < m, x₀ < m. 

Квадратичная конгруэнтная последовательность вида x_n+1=(bx_n²+ax_n+c)mod m

имеет период длинной m тогда и только тогда, когда

1.  с и m взаимно простые числа;

2.  b и a-1 кратны р для всех р – нечетных простых делителей m;

3.  b четно и b=a -1 (по mod 4) если  m кратно 4;

b=a –1 ( по mod 2) если m кратно 2;

4.  b<>3c (по mod 9 ) если m кратно 9;

Для третьего метода оптимальным значением x₀ является число равное примерно 1/10 объема выборки.