Моделирование произвольно распределенных непрерывных псевдослучайных величин

Министерство Образования РФ

НГТУ

кафедра прикладной математики

Лабораторная работа №2

По курсу «Моделирование и управление в экономике»

Факультет: ПМИ

Группа: ПМ-06

Бригада №7

Студентка: Кудрявцева М. А.

Преподаватель: Чимитова Е.В.

Новосибирск 2004г.

Моделирование произвольно распределенных непрерывных псевдослучайных величин

Цель работы.

Изучение методов, разработка и реализация алгоритмов имитации непрерывных псевдослучайных величин с произвольным законом распределения. Статистический анализ качества псевдослучайных последовательностей.

Вариант задания.

Найти методом обратной функции моделирующее выражение для случайной величины , имеющей распределение Вейбулла. Реализовать алгоритм моделирования последователь-ности случайных величин . С помощью программной системы ISW "Интервальная статистика" осуществить статистический анализ полученной выборки псевдослучайных величин.

,

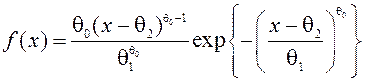Выполнение.

Ø  Определение методом обратной функции моделирующего выражения для случайной величины .

Ø  Реализация алгоритма моделирования последовательности случайных величин .

Моделирование последовательности случайных величин производилось следующим образом (случайная последовательность состоит из 1000 значений):

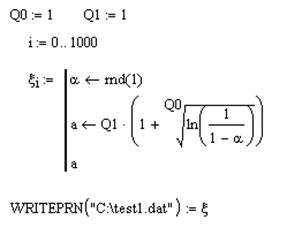
Ø  Статистический анализ полученной выборки псевдослучайных величин с помощью программной системы ISW "Интервальная статистика".

С помощью программной системы ISW проводилась проверка простой гипотезы о согласии. Были использованы следующие критерии: отношения правдоподобия,        - Пирсона, Колмогорова, Смирнова, - Мизеса, - Мизеса. При группировании выборка разбивалась на 10 интервалов. Таким образом, были получены следующие результаты.

Уровень значимости (вероятность ошибки первого рода) a= 0.01   

Достигаемый уровень значимости (вероятность согласия) P=1-G(S|H0)= 0.19884

P>a: гипотеза о согласии НЕ ОТВЕРГАЕТСЯ

Результаты проверки согласия: k=10, r=0

Отношения правдоподобия S=16.917   P=0.050025

Хи-квадрат Пирсона S=18.877   P=0.026261

Колмогорова S=0.87344  P=0.43043

Смирнова S=2.9359   P=0.2304 

Омега-малое кв. Мизеса S=0.16054  P=0.35899

Омега-большое кв. Мизеса S=1.9575   P=0.096921

Гистограмма имеет вид:

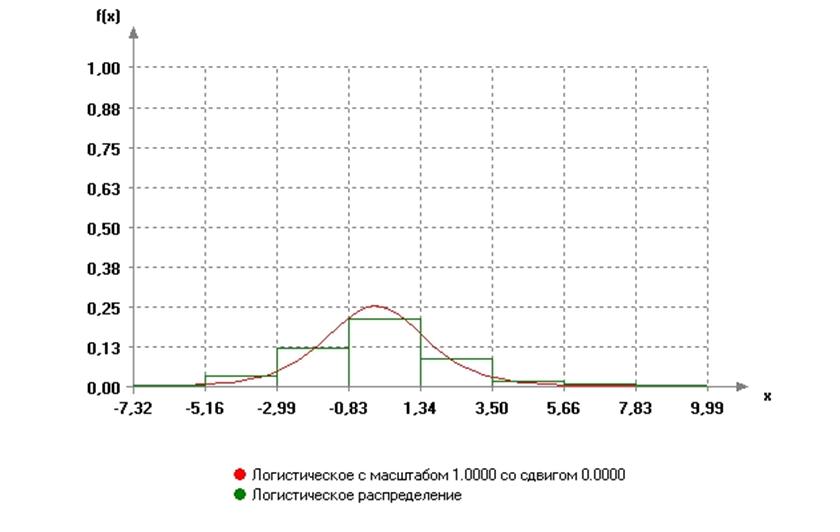
График функции распределения имеет вид:

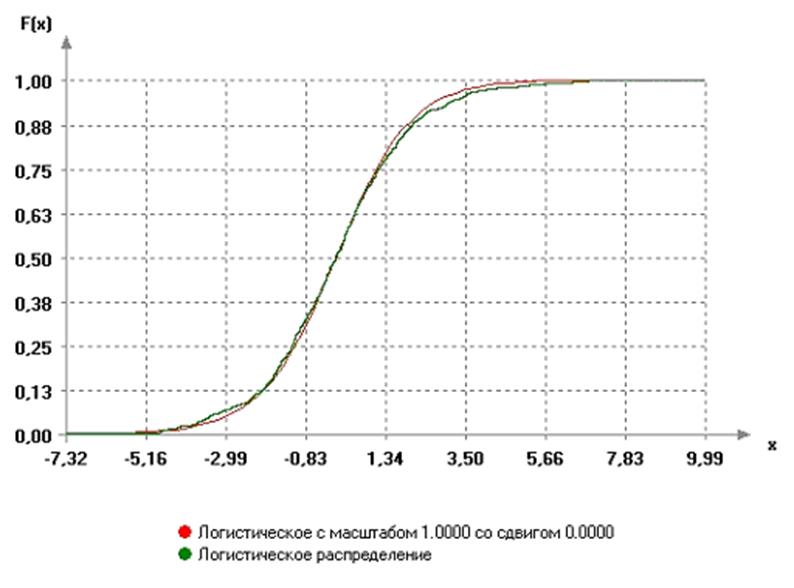
Вывод.

Как видно из проведенных исследований, сгенерированная последовательность соответствует логистическому распределению.