Моделирование последовательности дискретных случайных величин, имеющих пуассоновское распределение

1.  Задание

Смоделировать последовательность дискретных случайных величин, имеющих пуассоновское распределение, и исследовать на принадлежность Пуассоновскому распределению по критерию c² -Пирсона.

2. Постановка задачи

1.         Генерация случайных величин с Пуассоновским распределением.

Вероятность того, что случайная величина x равна целому неотрицательному числу m вычисляется так:

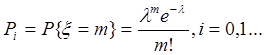           (1)

Для того чтобы получить случайную величину x Ро(λ), воспользуемся следующей теоремой:

Если a – случайная величина с распределением Rav[0,1] и P_m=P{x_m=m}, m=0, 1, 2, …, то выполняется: P_m=P{}.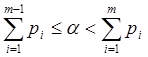

Т.е. при известном a Rav[0,1] можно получить случайную величину x, которая принимает найденное по теореме значение m. Причем, если случайная величина a хорошо смоделирована, то и случайная величина x тоже хорошо смоделирована.

1.         Генерация равномерно распределенных величин.

В качестве генератора равномерно распределенных случайных величин будем использовать следующий метод:

           (2),

Данный метод позволяет получать последовательности случайных величин, хорошо распределенных на отрезке .

3.         Проверка данных на согласованность с Пуассоновским распределением.

Для проверки полученной выборки будем использовать критерий  - Пирсона:

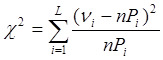        (3),

где L – количество различных значений в выборке,

 - частота с которой встречается фиксированный элемент выборки,

- теоретическая вероятность фиксированного элемента,

a – вероятность отвергнуть данные при условии, что они верны (a очень маленькое и называется уровнем значимости критерия)

n – объем выборки.

Далее сравниваем полученное значение выражения (3) и значение квантиля -распределения порядка (1-a) c (L-1) степенями свободы. И если значение выражения (3) оказывается меньше, чем значения квантиля, то выборка имеет Пуассоновское распределение.

2.  Результаты исследований.

Покажем зависимость характера выборки от l при разных объемах.

Тест1.

a=0.1    N=100

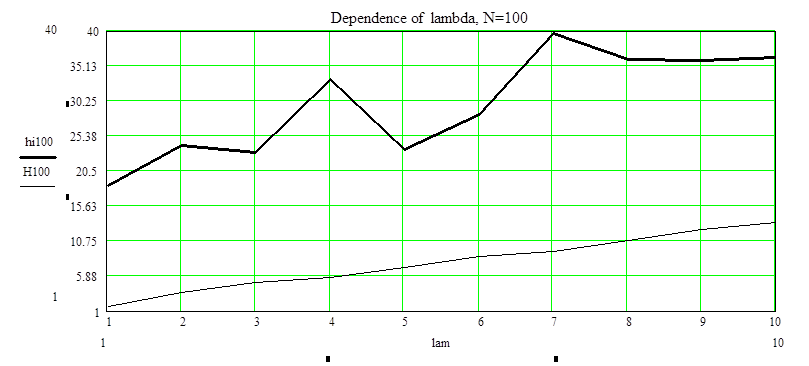
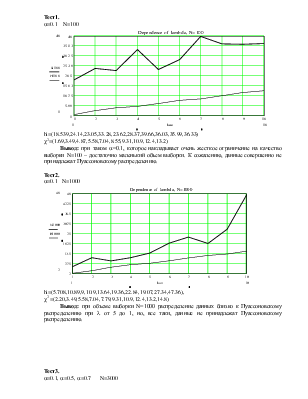
hi=(18.539,24.14,23.05,33.28,23.62,28.37,39.66,36.03,35.99,36.33)

c²=(1.69,3.49,4.87,5.58,7.04,8.55,9.31,10.9,12.4,13.2)

Вывод: при таком a=0.1, которое накладывает очень жесткое ограничение на качество выборки N=100 – достаточно маленький объем выборки. К сожалению, данные совершенно не принадлежат Пуассоновскому распределению.

Тест2.

a=0.1   N=1000

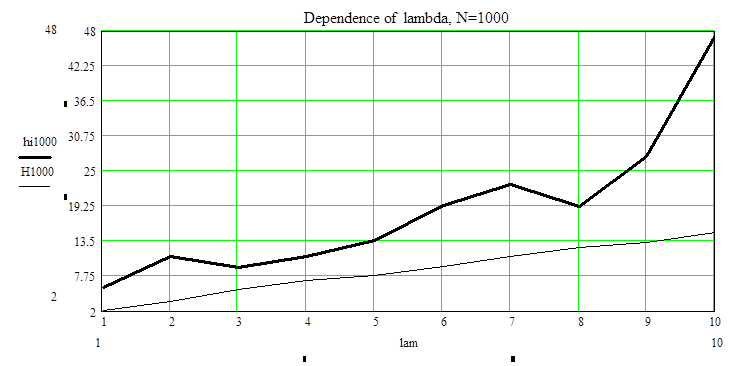
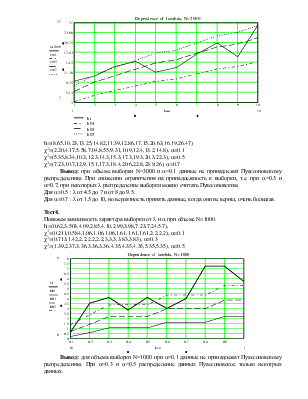
hi=(5.708,10.89,9,10.9,13.64,19.36,22.84,19.07,27.34,47.36),

c² =(2.20,3.49,5.58,7.04,7.79,9.31,10.9,12.4,13.2,14.8)

Вывод: при объеме выборки N=1000 распределение данных близко к Пуассоновскому распределению при l от 5 до 1, но, все таки, данные не принадлежат Пуассоновскому распределению.

Тест3.

a=0.1, a=0.5, a=0.7      N=3000

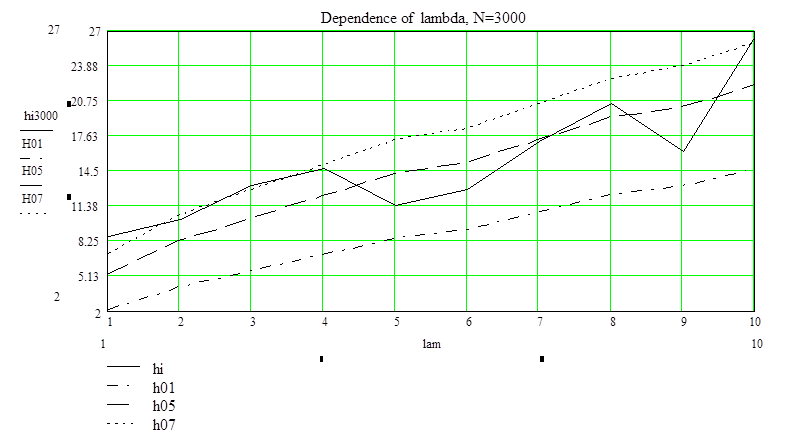
hi=(8.65,10.23,13.25,14.82,11.39,12.86,17.15,20.63,16.19,26.47)

c²=(2.20,4.17,5.58,7.04,8.55,9.31,10.9,12.4,13.2,14.8), a=0.1

c²=(5.35,8.34,10.3,12.3,14.3,15.3,17.3,19.3,20.3,22.3), a=0.5

c²=(7.23,10.7,12.9,15.1,17.3,18.4,20.6,22.8,23.9,26), a=0.7

Вывод: при объеме выборки N=3000 и a=0.1 данные не принадлежат Пуассоновскому распределению. При снижении ограничения на принадлежность к выборки, т.е. при a=0.5 и a=0.7, при некоторых l распределение выборки можно считать Пуассоновским.

Для a=0.5 : l от 4.5 до 7 и от 8 до 9.5.

Для a=0.7 : l от 1.5 до 10, но вероятность принять данные, когда они не верны, очень большая.

Тест4.

Покажем зависимость характера выборки от l и a при объеме N=1000.

hi=(0.62,3.503,4.09,2.85,4.10,2.99,3.98,7.23,7.24,5.7),

c²=(0.211,0.584,1.06,1.06,1.06,1.61,1.61,1.61,2.2,2.2), a=0.1

c²=(0.713,1.42,2.2,2.2,2.2,3,3,3,3.83,3.83), a=0.3

c²=(1.39,2.37,3.36,3.36,3.36,4.35,4.35,4.35,5.35,5.35), a=0.5

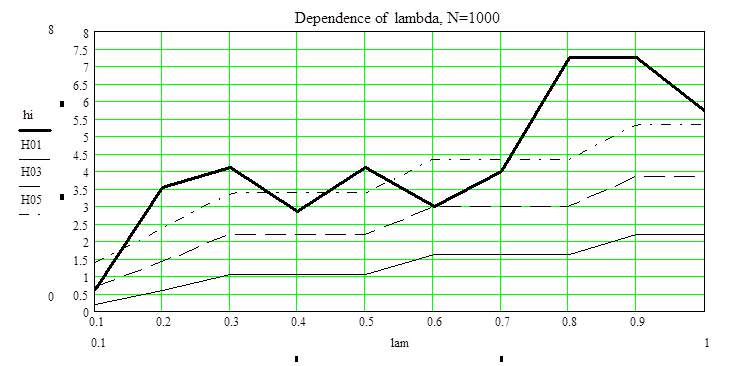
Вывод: для объема выборки N=1000 при a=0.1 данные не принадлежат Пуассоновскому распределению. При a=0.3 и a=0.5 распределение данных Пуассоновское только некотрых данных.

Общий вывод:

Данные моделируются с распределением зачастую отличным от Пуассоновского, но можно подобрать параметры, когда они все таки принадлежат Пуассоновскому распределению. Также СВ x, которая должна изменяться в пределах [0,µ], принимает значения не более, чем 24, что далеко от µ. Причина, видимо, в не очень хорошо смоделированных значениях aÎRav[0,1] и в том, что не хватает 6 знаков (a=0.******) для моделирования больших чисел.